金融时间序列的短期相依性研究

易文德

(重庆文理学院 数学与统计学院,重庆 402160)

●财经透视

金融时间序列的短期相依性研究

易文德

(重庆文理学院 数学与统计学院,重庆 402160)

金融资产相依结构的研究在金融风险分析中有着重要的意义。金融资产的相依结构主要有两类:一类是单个金融资产自身时间前后交易价格波动的相依关系,称为短期相依关系,另一类是金融资产间的价格波动相依结构,称为同期相依关系。针对前一种相依关系,我们应用混合相依结构M-Copula函数模型对上海综合指数、香港恒生指数和美国道琼斯指数三种金融时间序列前后一个交易日的价格波动相依关系进行了分析。应用两步骤法对模型的参数进行估计,并对边缘分布和M-Copula模型进行了拟合优度检验。结果表明:混合M-Copula模型能够捕捉金融资产时间序列的短期相依关系的变化规律。

短期相依;Copula函数;时间序列;尾部相关

相关性在金融分析中非常重要。线性相关系数、Granger因果分析方法是常用的相关性分析方法,但它们都存在一定的局限性[1,2]。金融时间序列通常表现为高峰、厚尾分布,它们的方差有时并不存在。因此线性相关系数不能用来反映其相关性,而且对非线性相关关系更是无能为力。Granger因果关系检验通常只能给出定性的结论而不能给出定量描述。

Copula函数是一个具有均匀边缘分布的多元分布函数,由 Sklar定理[3]可知,当模拟多元分布函数时,可以通过分别模拟其边缘分布和 Copula函数来实现,而 Copula函数能捕捉到多元分布所有的相依关系。由于 Copula函数在捕捉时间序列相依结构时表现出来的优越性和灵活性,在金融和保险等领域得到广泛应用。Frees andValdez(1998)[4]和 Embrechts等 (2002)[5]研究了时间序列间相依结构的模拟和估计。

在时间序列相关性的 Copula函数方法模拟中,Copula函数确定了时间序列间的多维分布函数,基于 Copula函数的时间序列模型能够捕捉边缘分布和相依结构的多种特性 (如边缘的偏度性和厚尾性,相依结构的集聚性、上下尾相依性)。

Darsow等(1992)[6]给出了马尔科夫序列的充分必要条件,Joe(1997)[7]提出了一类基于参数 Copula函数和参数边缘的参数平稳马尔科夫模型,并应用于空气质量的度量。YI和Liao(2010)[8]结合短期相依和同时相依关系建立了时间序列相依结构模型并提出了三个阶段参数极大似然估计方法。

模拟单个时间序列的时间短期相依性与模拟多个时间序列间的相依性同样重要,在不能确定线性相关系数能否正确度量单个序列的时间短期相依关系时,采用更灵活和稳健的相依分析技术——Copula函数方法分析序列的时间短期相依结构更为可靠[9]。近年来,Copula函数被广泛用来研究随机变量间的相依关系,易文德 (2010)[10]应用 Copula函数研究了股市交易量与股价的相依关系。本文结合一元半参数马尔科夫时间序列建立基于 Copula函数的时间短期相依模型,并以上证 A股综合指数 (SH)、香港恒生指数 (HK)、美国道琼斯指数 (DJ)为研究对象,分析各金融资产时间序列的时间短期相依关系。

一、基于 Copula函数的风险相依性分析

由 Sklar定理[3]:Copula函数是把两个或多个随机变量ξ1,…,ξn的联合分布 F(x1,…,xn)与它们的边缘分布 Fξ1(x1),…,Fξn(xn)相连接 ,它使 F(x1,…,xn)=C(Fξ1(x1),Fξ2(x2),…,Fξn(xn))等式成立,其中 Copula函数从概率的角度描述了变量间的相依结构。这里对边缘分布和联合分布没有限制,而且对变量作单调增变换,相应的 Copula函数以及由它导出的一致性和相关性测度 (如由 Copula函数导出的Kendall的τ、Spear man的ρ以及 Gini系数)不会改变,这与线性相关系数相比,应用范围更广,实用性更强[3]。应用Copula函数模型研究复杂的金融时间序列的相依性和风险具有很大的优越性,可以更广泛、更准确的捕捉各种金融资产的相依信息,它既可以捕捉到变量间静态的相依关系还可以捕捉到动态的、非对称的以及分布尾部的相依结构。

在金融风险分析中度量组合资产的相依性风险时,由于计量方法的局限性,通常假设各金融资产的风险因子的联合分布服从多元正态分布,但大量实证表明,这种假设与客观事实相违背,金融资产时间序列通常都呈尖峰厚尾性。因此,在正态分布假设下进行的组合资产相依性风险分析与实际情况有较大的偏差。通过 Copula函数模型可以将风险分解成单个资产的风险和资产组合风险两部分,单个资产风险由其边缘分布完全描述,而资产组合产生的风险完全由连接各资产的 Copula函数来刻画。这样可以简化建模过程和有利于相依风险问题的分析理解。假设 X和 Y表示两种金融资产损失的时间序列,单个资产的风险由边缘分布 u=F(x)和 v=G(y)完全描述,而组合资产投资风险由 Copula函数 C(u,v)来刻画,其相依性不变的测度 Kendall的τ、Spear man的ρ可分别表示为:上下尾部相依系数刻画了组合资产典型事件等极端情况的相依程度。运用 Copula函数理论研究组合投资风险可以提高风险度量的准确性和有效性,达到预测、控制和防范风险的目的。

二、马尔科夫 (Markov)时间序列 M-Copula函数模型的构建

设 {Xt,t=1,2,…}由 (F(·;θ),C(·,·;δ))生成的一阶平稳马尔科夫时间序列,其中 F(·;θ)是连续的边缘分布函数,密度函数 f(·;θ)是实数域上的 Lebesgue测度;C(·,·;δ)是关于 (Xt-1,Xt)的连续的 Copula函数,密度函数 c(·,·;δ)是 (0,1)2上的 Lebesgue测度 ,θ,δ分别是边缘分布和 Copula函数的有限维参数。由 Sklar定理[3]:H(x,y;θ,δ)=C(F(x;θ),F(y;θ);δ)是一个具有边缘分布为 F(·;θ)的联合分布函数。Joe(1997)[7]应用 Copula函数模拟了马尔科夫时间序列的相依关系。联合分布为 H的平稳马尔科夫时间序列的转移概率密度函数可表示为:

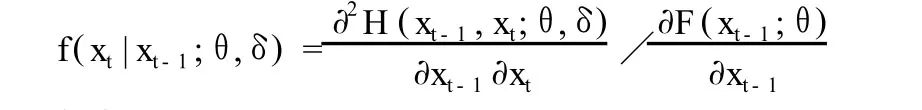
上式可以等价表示为:

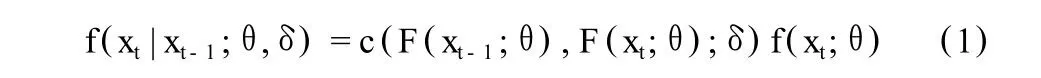
由 (1)式可知,平稳马尔科夫时间序列完全由边缘分布和Copula函数确定。

Fentaw Abegaz[11]研究了两阶段极大似然估计及其估计的一致性和近似正态性。Chen[9]研究了两阶段半参数极大似然估计及其估计的一致性和近似正态性。

运用 Copula函数技术构建金融时间序列模型,主要解决三个关键问题:(1)确定边缘分布;(2)选取能很好描述边缘分布相依结构的 Copula函数;(3)模型参数的估计和对模型的拟合优度检验。

由于金融时间序列具有尖峰、厚尾现象,不服从正态分布。边缘分布用 t分布刻画:

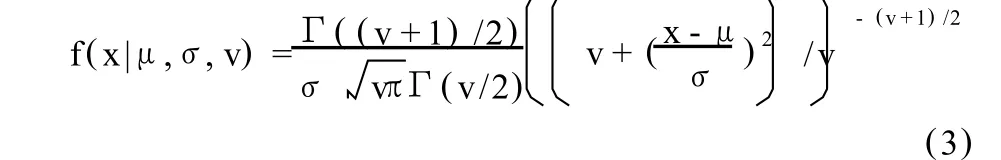
其中μ、σ和 v分别是 t分布的位置参数、形状参数和自由度参数。

为了刻画金融时间序列短期相依的尾相依及其非对称性,用混合 Copula模型描述金融时间序列的短期相依结构。其表达式为:

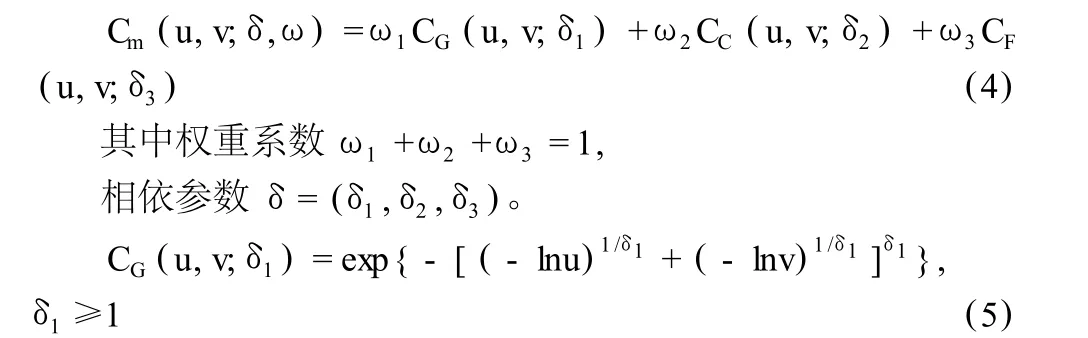
叫 Gumble Copula函数,其相依结构呈非对称性,表现出上尾厚下尾薄的特点。参数δ1值越大,表明金融时间序列短期相依程度越高。当δ1→1时,CG(u,v;δ1)=uv,表示金融时间序列短期相互独立。

称为 Frank Copula函数,当δ3大于零,表示上尾相关;当δ3小于零,表示下尾相关;当δ3趋于零时,表示两变量独立。因此,Frank Copula函数能捕捉金融时间序列的上尾相依和下尾相依性。

对金融时间序列短期相依模型的拟合优度检验,采用χ2检验方法。构造χ2统计量:把区域 [0,1]×[0,1]分成 m ×m个单元格,记第 i行第 j列的单元格记为 Aij,i,j=1,…,m。设Oij,Eij(^δ)分别是数据点落在单元格Aij中的观察点数和由模型 (4)计算预测的数据落在单元格 Aij中的频数。

三、三个股票市场短期相依结构的实证分析

中国股票市场是一个新兴的发展中的资本市场,交易规则和监管制度有待规范。为考察中国股票市场与成熟的股票市场的各自身短期的相依结构,我们选择上证综合指数(SH)、香港恒生指数 (HK)和道琼斯工业指数 (DJ)的每日收盘价为样本。将价格 {Pt}取为各股票市场的第 t日的指数收盘价,将收益率 {Rt}定义为 Rt=100·(lnPtlnPt-1),t=1,…,T。样本区间从 1997年 1月 2日到 2008年12月 31日,由于各市场的假日不同,经处理后各市场的数据个数是不同的,上证综合指数收益率序列样本数为 2887个,香港恒生指数收益率序列样本数为 2956个,道琼斯工业指数收益率序列样本数为 3016个。表 1是三个序列的描述性统计特征。从表 1中的 Jarque-Bera值可知三个序列都拒绝正态分布假设;从偏度 (Skewness)和峰度 (Kurtosis)来看,三个序列均存在尖峰、厚尾特征;对三个收益率序列进行Ljung-Box(20)测试,发现三个序列均拒绝无自相关性;对三个序列进行单位根检验发现它们拒绝有单位根,因此都是平稳时间序列。

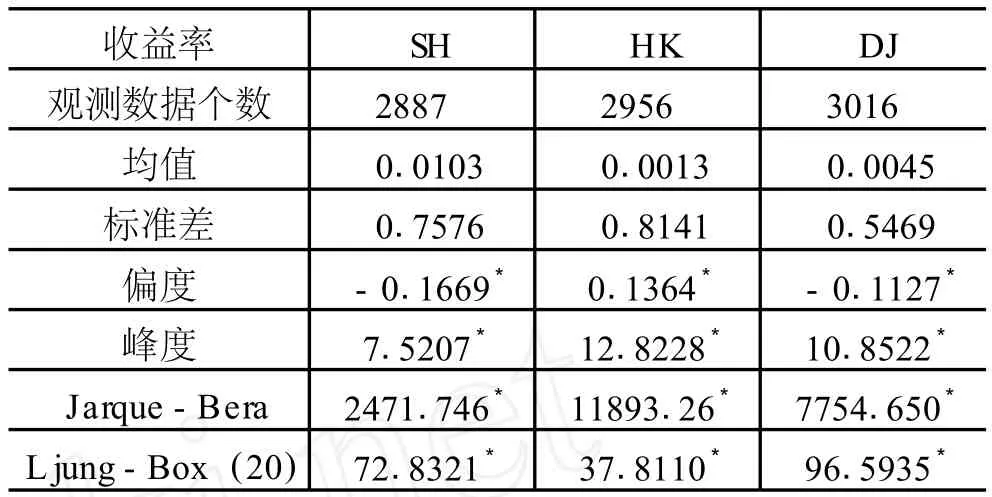
表1 三个股票市场指数收益率统计描述

(一)边缘分布模型的估计

模型的参数估计采用二步极大似然估计法,在建立MCopula模型之前,首先对边缘分布中的参数进行估计。由于对模型的拟合优度检验是采用χ2检验方法,因此,模型的半参数估计方法 (即边缘用非参数方法而 Copula函数用参数方法)将会使χ2检验方法失效[12]。在我们的分析中,边缘的估计用极大似然估计方法而不能采用经验分布。表 2为边缘分布模型的参数估计值,然后将参数值代入 (3)式中,得到边缘分布模型。图 1是边缘分布模型概率积分变换后与(0,1)均匀分布的 QQ图,对变换后的序列进行序列相关检验接受无序列相关假设,图形表明边缘分布能够反映三个序列的分布特征。

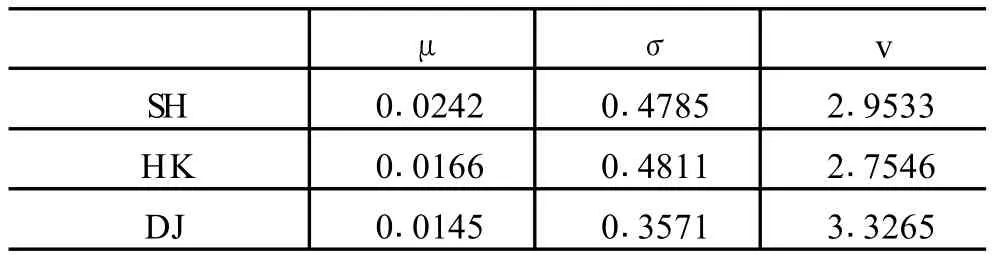
表2 边缘分布的参数估计

(二)暂时性混合相依结构M-Copula模型的估计

前面已经估计了收益率 {Rt},t=1,…,T的边缘分布,在此基础上再研究 {Rt-1,Rt}的相依结构。在用暂时性混合相依结构M-Copula模型拟合实际数据之前,可以算得三个金融时间序列的暂时性线性相关系数分别为ρSH=-0.0099、ρHK=-0.0071和ρDJ=-0.0597;可以看出各金融时间序列的暂时性相关都较小,而且呈现为负相关的特点。在混合M-Copula模型中,有 5个参数需要估计,首先用边缘分布式对各收益率 {Rt}进行概率积分变换,得到三个新序列 {u1t},t=1,…,2887、 {u2t},t=1,…,2956和 {u3t},t=1,…,3016。用每个序列的一阶马尔科夫序列向量 (ut-1,ut),图 2给出了三个序列的一阶马尔科夫序列向量的散点图。

用极大似然估计方法对混合M-Copula模型中的相关参数及权重参数进行估计,估计结果在表 3列出。

图2 序列与其滞后一期的概率积分变换后的散点图

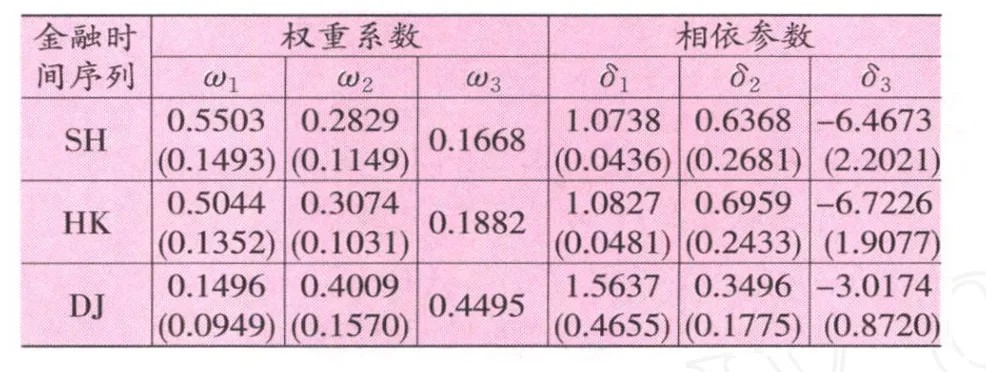
表3 混合M-Copula模型的参数估计值

从表 3中可以看出,金融序列 SH和 HK的相依结构非常相近,权重系数和相依参数都非常接近,Gumbel Copula在混合相依结构模型中所占的比重较大,但其对应的相依参数非常接近于 1,虽然 Frank Copula在混合相依结构模型中所占的比重较小,但其对应的相依参数小于 0,表现为下尾相依性。金融序列DJ的相依结构明显与前两序列的相依结构有差别,Clayton Copula和 Frank Copula在混合相依结构模型中所占的比重比较接近且大于 Gumbel Copula在混合相依结构模型中所占的比重,明显表现为下尾相依性。研究金融时间序列的暂时性相依结构时,应该综合考虑混合相依结构模型中的权重系数和具有各种不同相依特征的 Copula的相依参数的值。图 3给出了各金融时间序列暂时性相依结构的直观图形,为了便于对比,给出了各金融时间序列 (ut-1,ut)的经验 Copula及M-Copula的概率密度分布图,从图形上可以观察到各组图形基本上是一致的,均出现下尾高、上尾低的非对称的正负混合相依的特点。

从图 3中可以看各金融时间暂时性相依结构是复杂的,当然形成这种复杂相依结构的原因也是多方面的,我们可以从投资者的角度对这种相依结构进行一定的解释:三种金融时间序列的暂时性相依都表现为混有正相依和负相依的混合相依特征;正相依结构反映在证券交易时表现为今天下跌而明天也下跌、或今天上涨而明天也上涨的连续惯性,说明投资者有追涨杀跌的交易行为;而负相依结构反映在证券交易时今天下跌而明天上涨、或今天上涨而明天下跌的交替性,说明投资者有下跌补仓和获利了结的投资行为,投资策略表现为波段操作的技术手段。但对于比较大的利空和利好消息,也反映出投资者跟风的心里。对较大的利空市场出现暴跌行情时,投资者会感到恐慌,会采取跟风杀跌的行动;而对于较大的利好消息市场出现暴涨行情时,投资者又会采取跟风追涨的投资行动,但杀跌和追涨的尾部相依性又表现出非对称性,即对等量利空和利好,杀跌和追涨的程度不一样。从各图形的相依结构中我们基本能读懂图形反映的信息。

(三)暂时性相依结构 M-Copula模型的拟合优度检验

根据上面介绍的拟合优度检验的方法,χ2检验的基本原理,构造单元格表格,对表格的构造我们选取了 8×8、10×10、12×12、16×16和 20×20五种情况。对每种情况计算出落在每个单元格内的实际观测频数以及由模型预测的落在单元格内的预测频数,并把单元格观测频数小于 5的单元格合并。表 4列出了各种情况算得的χ2统计量,临界值是在显著性水平为 1%下的值。从χ2统计量的值可以看出,三个金融时间的暂时性相依结构M-Copual模型在各种不同单元格的划分情况下通过显著性水平检验,认为模型以刻画金融时间序列的暂时性相依结构。

由暂时性相依结构M-Copula模型作概率积分变换得条件分布 F(xt|xt-1)序列,并对其进行序列相关性检验,不能拒绝无自相关性,其对 (0,1)上的均匀分布的 QQ图如图 4,认为服从均匀分布。从这方面认为模型能刻画各金融时间序列的暂时性相依结构。

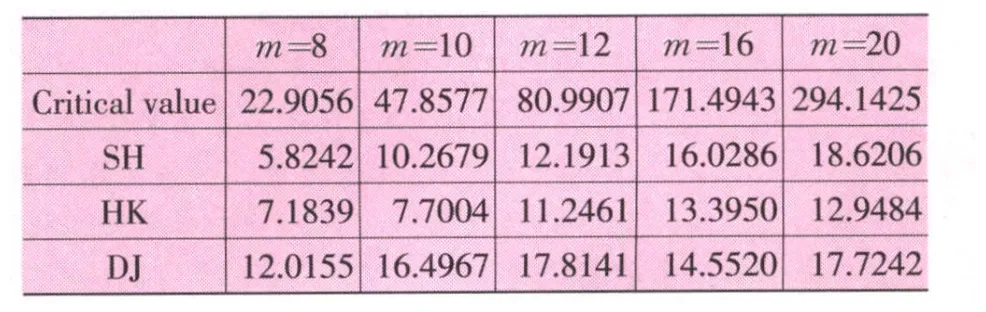
表4 χ2检验统计量

四、结 论

金融资产时间序列的相依结构研究是风险分析研究的重要内容。时间序列的相依关系主要有两类:一类是单个金融资产本身时间前后交易形成的相依关系,即本文研究的暂时性相依关系;另一类是一个金融资产与另一个金融资产之间的同期相依关系。近几年对资产间相关结构的研究吸引了许多学者广泛的兴趣,对金融资产时间序列自身的相依结构的研究为数不多。

本文提出了一个基于 Copula函数方法M-copula模型研究金融时间序列暂时性相依结构,旨在反映金融资产自身的相依模式和相依程度。混合M-copula模型能克服对金融资产相依结构描述的单一性,既能捕捉上尾相依及下尾相依的非对称的尾部变化规律,又能捕捉正相依或负相依的中部变化结构。我们对上海综合指数、恒生指数和道琼斯指数三个股票市场进行实证研究表明,三个股票市场的暂时性相依结构大体上类似而程度上存在一些差异,都表现为正相依和负相依两种相依结构的混合以及上尾高下尾低的非对称的尾部相依关系。正相依和负相依的相依结构反映了投资者不同的投资行为。

金融市场风云莫测,变化多端,受国内国际以宏观和微观等诸多因素的影响,这造成了金融市场相依变化的复杂性和不确定性。函数 Copula的性质给研究相依性关系带来了极大的灵活性,不象传统的多维分布对边缘分布有严格的限制,Copula函数可以灵活选择边缘分布的形式,函数本身种类繁多,变化多样,可以通过选取适当 Copula函数和边缘分布进行组合建立模型以捕捉金融资产时间序列复杂的相依结构和相依程度。

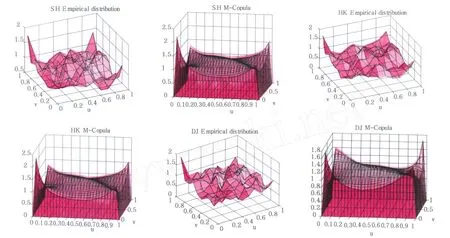
图3 经验分布和M-Copula模型的概率密度图

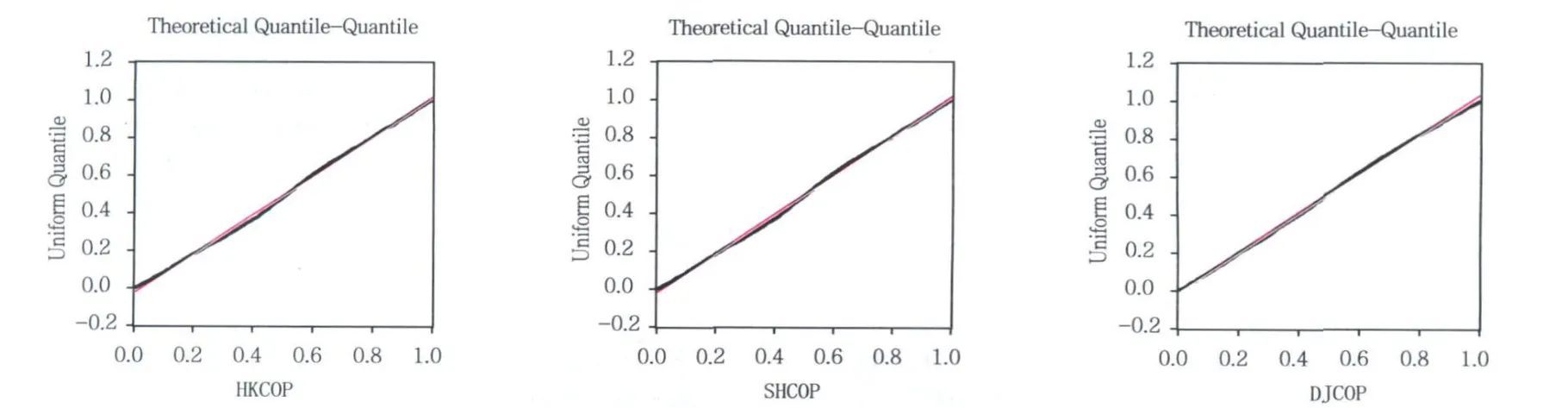
图4 条件分布序列对 (0,1)均匀分布的 QQ图

[1]张尧庭.我们应该选用什么样的相关性指标? [J].统计研究,2002,(9):41-44.

[2]史道济.相关系数与相关性 [J].统计科学与实践,2002,(4):22-24.

[3]Nelsen R.An Introduction to Copulas[M].New York:Springer,1999.

[4]Frees EW,Valdez EA.Understanding Relationships Using Copulas[J].North American Actuarial Journal,1998,2:1-25.

[5]Embrechts P,MeNeilA,Straumaann d.Correlation and dependence Properties in Risk Management:Properties and Pitfalls[M].Cambridge:Cambridge University Press,2002.

[6]Darsow W,Nguyen B,Olsen E.Copulas and Markov processes[J].Illinois Journal ofMathematics,1992,36:600-642.

[7]Joe H.Multivariate Models and Dependence Concepts[M]:Chapman&Hall/CRC,1997.

[8]YiW D,Liao S S Y.Statisticalpropertiesof parametric estimators for Markov chain vectors based on copula models[J].Journal of Statistical Planning and Inference,2010,140(6):14965-1480.

[9]Chen X,Fan Y.Estimation of Copula-based Semiparametric Time Series Models[J].Journal of Econometrics,2006,130:307-335.

[10]易文德.基于 Copula函数模型的股市交易量与股价相依关系 [J].系统工程,2010,28(10):36-41.

[11]Abegaz F,Naik-Nimbalkar UV.Modeling Statistical Dependence ofMarkov Chains via Copula Models[J].Journal of Statistical Planning and Inference,2008,138:1131-1146.

[12]Roch O,Alegre A.Testing the Bivariate Distribution of Daily Equity ReturnsUsing Copulas.An Application to the Spanish StockMarket[J].Computational Statistics&Data Analysis,2006,11(7):1-18.

[责任编辑:张 青]

Study on the TemporalDependence of Financial T ime Series

YIWen-de
(School of Mathematics&Statistics,Chongqing University of A rts and Sciences,Chongqing402160,China)

It is greatly interesting to investigate the dependence structure of financial assets in financial risk analysis.There are two types of dependence structures of financial assets:one is the dependence relationship of individual financial asset itself in different timewhich is called temporal dependence relationship and the other is the dependence structure between different financial assets which is defined as contemporaneous dependence.In this paper,we focus on the former and propose aM-Copula model to investigate the temporal dependence for three stockmarkets:the ShanghaiComposite Index(SH),the Hang Seng Index(HK)andDow-Jones Index(DJ).The twostage max imum likelihood estimation is employed to est imate the parameters of model and the goodness of fit of margins and M-Copula model are tested.The results show that theM-Copula modelmay capture the temporal dependence structure of financial time series.

temporal dependence;copula function;time series;tail dependence

F830

A

1007—5097(2011)03—0071—05

10.3969/j.issn.1007-5097.2011.03.017

2010—12—22

教育部人文社会科学研究项目 (08JA790142);重庆市教育委员会科学技术研究项目 (kj081214)

易文德 (1965—),男,江西宜春人,副教授,博士,研究方向:概率统计,经济计量和金融风险。

图1 三序列概率积分变换后的 QQ图