财政分权下中央及地方政府实现经济增长的模型研究
2011-11-01杜超焦文超
杜超,焦文超
(1.山东大学经济学院,济南,250014;2.山东财政学院,济南250014)
财政分权下中央及地方政府实现经济增长的模型研究
杜超1,焦文超2
(1.山东大学经济学院,济南,250014;2.山东财政学院,济南250014)
文章采用博弈理论研究了财政分权下中央及地方政府实现经济增长的策略分析,分别构造了中央政府与地方政府之间的博弈模型以及地方政府与地方政府之间的博弈模型。由中央政府与地方政府之间的模型分析可知,如果地方政府与中央政府的目标函数不一致,地方政府最优投资总量就会高于中央政府的意愿投资总量。并且地方政府投资所达到的经济增长无法实现中央政府预想的经济增长度。由地方政府与地方政府之间的模型分析可知,地方政府双方合作时使得收益最大、投资最小,这种“双赢”的合作应该是他们的最佳选择。
财政分权;博弈论;政府;经济增长
0 引言
现实中,随着中国经济的持续快速增长和融入全球化的步伐加快,国内各地方政府之间为争取自身有利的发展条件和优势地位,提升本地区的经济水平,在要素资源、基础设施、政策环境、政府形象等诸多领域不断展开竞争。地方政府间的这种竞争行为是非常复杂的,但是对经济利益的追求是构成地方政府行为的一个重要动力。正因为如此,在学术界,这个问题也展开了一些讨论。
本文在前人研究的基础上,借鉴学者们现有的研究成果,采用博弈论的研究方法构建了中央政府与地方政府、地方政府与地方政府之间的博弈模型,通过分析模型最优均衡解,揭示政府之间的投资行为对促进经济增长的影响。
1 模型说明
在模型中,假设:
(1)中央政府和地方政府具有追求经济增长的强烈意愿,经济增长是政府政绩和执政能力的最重要体现之一。对地方官员来说,则是决定其是否得到提升的关键指标。
(2)一般来说,政府换届前后的领导班子具有相对更高的经济增长目标追求,尤其是各级地方政府的新任领导人,都会将经济的更快增长作为目标。
(3)对地方政府领导人来说,经济增长收益主要是增加投资和经济发展给地方政府带来的直接收益。
(4)为实现快速的经济增长,在投资、消费、出口三因素中,地方政府最容易影响的变量是投资。尤其是在有限的任期内,追求多投资是短期内促进经济增长最直接和有效的手段。
(5)假定产业的市场容量有限的情况下,中央及地方政府对某一产业进行投资。
假定整个经济由两个地区组成,有两个平级的地方政府i(i=1,2),地方政府的核心目标是促进经济增长,其中主要工作是直接或间接拉动当地投资增长。下面考擦在假定某一个产业市场容量有限的情况下,地方政府1与地方政府2均对该产业进行投资,设地方政府的投资量为gi,则全社会投资总量为G(G=g1+g2)。显然,任何一方的收益都会受到该产业市场容量的限制,因此产业的市场容量就构成了一个强大有力的约束量,而该产业的市场容量实际上就是该产业的市场需求,假定全社会中,该产业的市场需求函数为:

其中Q为该产业市场容量,它可以通过全社会的总投资来实现;p为市场需求为Q时的产品价格。
假定地方政府对该产业的投资可以完全相互替代。在产业的市场需求量为时,设单位投资产生的产量为k(k>0),则地方政府i投资gi所产生的产量为kgi,全社会投资总量G所产生的产量为:

因为产业的市场容量Q可以通过全社会的总投资来实现,所以假定:

可以看出,当(3)式成立时,全社会总投资所产生的产量正好为产品的市场需求量,供需均衡,产业市场达到均衡状态。
假设c(c>0)为投资的单位成本(成本包括投资增长可能引起的直接或间接的各种成本或损失,例如筹资成本,投资快速增长带来货币供给量增长导致的通货膨胀、金融风险隐患增加、影响经济平稳运行以及工业化所带来的生态破坏等)。假设地方政府i投资gi所产生的收益为πi,则πi=kgipcgi,联立(1~3)式,可得:
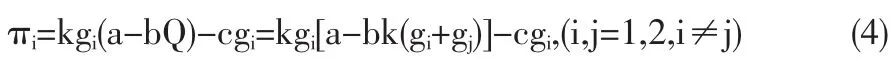
假设全社会投资所产生的收益为,则有:

下面分别分析中央政府与地方政府、以及地方政府之间的博弈。
2 中央政府与地方政府之间的模型
在考虑经济增长目标的博弈中,中央政府和地方政府都需要通过最大化自身收益来确定投资量。对中央政府而言,要确定全社会投资量G以到达社会收益最大化,根据(5)式,有:
由∂π/∂G=0,得到中央政府最优投资量为G*:

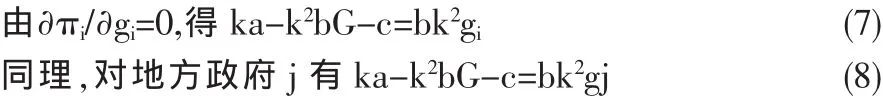
联立(7~8)式,可得地方政府1与地方政府2分散决策时,全社会的投资量G'为:

地方政府的最优投资量为g'=(ka-c)/3bk2,相应地方政府i的最大收益为π*=(ka-c)2/4bk2,此时相应的全社会的收益为
比较中央政府与地方政府的决策,不难发现:
(1)G* 这说明,地方政府各自决策确定的投资总量要高于中央政府意愿的全社会最优投资量。之所以出现此情况,原因在于地方政府并不承担由于其增加投资而带来的所有成本,而是可以将其中部分成本“外部化”,由整个经济体来承担,但中央政府在决策时则必须考虑到所有的成本。例如,中央政府在确定经济增长和投资目标时,会充分考虑实施这一目标是否会造成严重的通货膨胀,但地方政府则不会关注这一因素。 由G'=4G*/3可知,地方政府各自决策确定的投资量总和大于中央政府确定的最优投资量。这样的结果导致中央政府承担过大的投资成本,这导致社会福利损失,这包括经济过热、通货膨胀压力增大、经济系统稳定性下降、生态破坏和自然资源过度消耗等。要避免这样的后果,中央政府必须进行宏观调控,改变地方政府的投资策略。 (3)π'<π* 这表明,地方各自决策所得收益总和小于中央政府决策时所得收益。在财政分权下,虽然地方政府投资可以达到促进经济增长的目的,但是其促进经济增长的程度无法达到中央政府的要求,也无法实现中央政府预想的经济增长度。 在地方政府与地方政府只考虑地方政府经济增长目标时的博弈中,在假设信息结构是完全信息的情况下(即博弈双方对对方的收益都能够完全了解)予以分析。 在这个模型中,分两种模型:一种是合作模型,在这个模型中,两个地方政府相互合作,共同决策最优投资量,以期达到双方收益之和最大化;另一种是分散决策模型,在这个模型中,两个地方政府以达到自身的收益最大化为目标,各自独立决策。下面对这两种模型分别予以讨论。 在分散决策模型中,当两个地方政府同时投资某一产业时,他们取得的收益与他们投资的顺序有关。他们投资的顺序无非有两种:同时投资和抢先投资。如两个地方政府没有达成任何协议,同时投资该产业,则此时双方的决策构成cournot博弈;若两种地方政府中,一方抢先投资,另一方看到对方投资后,随后投资,此时双方的决策构成序贯理性的stackelberg博弈。 3.1.1 cournot博弈 在此模型中,两个地方政府同时投资该产业,两者独立决策,在决策时都没有考虑对方的决策。根据(4)式,地方政府1与地方政府2的收益函数分别为: 结论1:在cournot博弈中,地方政府1与地方政府2的最优投资量相等,为,两个地方政府的投资总量为;相应地,地方政府1与地方政府2的最大收益相同,为,两个地方政府的总收益为 3.1.2 stackelberg博弈 在stackelberg博弈中,假设地方政府1抢先投资,地方政府2随后投资。这样,地方政府率先决策投资量g1,地方政府2看到地方政府1的决策再确定自身的投资量g2,以期达到自身收益最大,而地方政府1在决策时也会考虑到地方政府2对自己决策的反应。采用逆向归纳法。 结论2:地方政府2投资决策对地方政府1的反应函数为 可见,g2是g1的减函数,这说明,当地方政府2看到地方政府1抢先投资后会减小自己的投资,并且地方政府的投资力度越大,地方政府2的投资力度越小。若地方政府1的投资刚好占领整个产业市场时,地方政府2会选择不投资,以免造成的投资损失。 将(10)式代入地方政府1的收益函数π2=kg1[a-bk(g1+g2)]-cg1,可得:berg博弈的均衡解,即结论3。 结论3:在stackelberg博弈中,地方政府1的最优投资量为,地方政府2的最优投资量为,两个地方政府的投资总量为;相应地,地方政府1的最大收益为,地方政府2的最大收益为,两个地方政府的总收益为 在此模型中,两个地方政府达成协议,成为同一个利益主体,共同控制各自的投资量,平分产业市场,共同决策双方的投资总量,以实现双方的收益总量最大化。即要求: s.t.g1=g2 结论4:在合作模型中,地方政府1与地方政府2的最优投资量相等,为,两个地方政府的投资总量为;相应地,地方政府1与地方政府2的最大收益相同,为,两个地方政府的总收益为 比较这三个模型的最优结果,可得: 从促进经济增长的角度出发,由(I)可看出,地方政府双方合作,经济增长是最快的,双方的总收益也最大,其次是两个地方政府没有任何协议的独立决策,即cournot博弈,最后是一方抢先投资的stackelberg博弈,但是在stackelberg博弈中,抢先投资的一方获得的收益最大。与其它模型比较,抢先投资对地方政府自身是最有利的,随后投资是最不利的,获得经济效益将最小;采取抢先投资的地方政府在双方合作的情况下也能达到在抢先投资时所取得的经济效果,即并且双方合作,使得采取随后策略的地方政府的收益也达到最大。而双方同时决策的cournot博弈模型,对想采取抢先投资的地方政府1来说,是经济增长效果最差的模型,而对地方政府2来言,cournot博弈模型却优于stackelberg博弈。 从投资的角度来说,在stackelberg博弈中,双方的投资总量最大,投资总量最小的是合作博弈模型。抢先投资对的地方政府1在stackelberg博弈中投资量达到最大,在合作博弈中投资量最小,而地方政府2却在stackelberg博弈中投资量最小,合作模型的投资量与在stackelberg博弈中的投资量相等,在cournot博弈中,地方政府2的投资量最大。 综合上述分析可看出,如果从追求本辖区经济利益最大化的角度出发,在产业市场容量有限的前提下,地方政府对某一产业投资的先后顺序,直接影响了博弈双方各自分得的产业市场份额的大小以及收益的高低,这正是目前地方政府竞相以增加投资支出的方式“争铺新摊子,争上新项目”现象的经济激励动因。 本文采用博弈理论研究了财政分权下中央及地方政府实现经济增长的策略分析。本文分别构造了中央政府与地方政府之间的博弈模型以及地方政府与地方政府之间的博弈模型。 由中央政府与地方政府之间的模型分析可得到结论:如果地方政府与中央政府的目标函数不一致,地方政府可以将经济增长中的部分成本外部化,那么地方政府最优投资总量就会高于中央政府的意愿投资总量,两者之差取决于地方政府可以外部化的增长成本的大小。存在外部性的情况下,地方政府的投资行为会导致社会福利的损失。并且地方政府投资所达到的经济增长无法实现中央政府预想的经济增长度。此时中央政府就需要通过宏观调控来保持经济平稳增长。 由地方政府与地方政府之间的模型分析可到结论:无论从投资还是从收益的角度看,地方政府双方合作时使得收益最大、投资最小,这种“双赢”的合作应该是他们的最佳选择。而在cournot博弈中,由于双方决策时均不考虑对方的策略,导致他们的投资多、收益小,可以说,这种盲目的决策是地方政府最差的策略。 但是这种同时决策的cournot博弈在现实中也是存在的,这就造成该产业多寡头垄断的局面,这种局面造成资源浪费,不利于加快地区经济的发展。而“双赢”的合作虽然是地方政府的最优选择,但是这种合作在现实中实现存在一定的难度,要解释这种现象,必须将分析的视角转入政治角度,即从地方官员个人晋升的政治博弈角度来进行解释。这也是下一步将要研究的方向。 [1]周业安.地方政府竞争与经济增长[J].中国人民大学学报,2003,(1). [2]夏杰长.地方政府:推动经济过热的重要因素[J].改革,2004,(5). [3]张晏,龚六堂.分税制改革、财政分权与中国经济增长[J].经济学(季刊),2005,(1). [4]张闫龙.财政分权与省以下政府间关系的演变——对20世纪80年代A省财政体制改革中政府间关系变迁的个案研究[J].社会学研究,2006,(3). [5]周黎安.中国地方官员的晋升锦标赛模式研究[J].经济研究,2007,(7). [6]朱恒鹏.分权化改革、财政激励和公有制企业改制[J].世界经济,2004,(12). [7]高鹤.财政分权、经济结构与地方政府行为:一个中国经济转型的理论框架[J].世界经济,2006,(10). [8]郭庆旺,贾俊雪.地方政府行为、投资冲动与宏观经济稳定[J].管理世界,2006,(5). [9]施锡铨.博弈论[M].上海:上海财经大学出版社,2000. F812 A 1002-6487(2011)07-0081-03 国家社会科学基金资助项目(06BJY103) 杜超(1972-),男,山东临沂人,博士研究生,研究方向:财政学。 (责任编辑/易永生)3 地方政府与地方政府之间的模型
3.1 分散决策模型
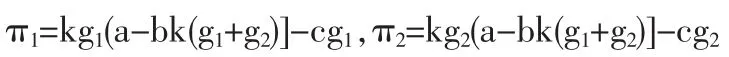

3.2 合作模型

3.3 模型比较

4 结束语
