区域物流系统发展的负熵机理及状态模型

张中强

（徐州工程学院管理学院，江苏徐州221008）

区域物流系统发展的负熵机理及状态模型

张中强

（徐州工程学院管理学院，江苏徐州221008）

文章首先界定了区域物流系统，把区域物流系统的组成要素分为物流基础、经济基础、基础环境。接着，运用协同学知识，分析了区域物流系统的负熵机理，并认为：要使区域物流系统驱向协同发展方向，必须使系统流出的熵大于流入的熵，即使系统获得负熵流，从而使系统的总熵下降，避免系统熵增加，导致系统出现无序状态。在此基础上，构建了区域物流协同状态模型，并介绍了模型的作用。

区域物流系统；负熵机理；状态模型

1 区域物流系统的构成

根据一般系统论，可以把区域物流系统的组成要素分为以下几个部分。具体组成如图1：

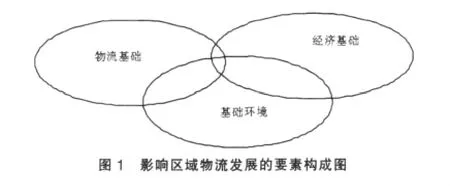
在影响区域物流发展的要素中，物流基础是在一定区域内，利用一定运载工具、在一定物流网络中为该区域提供人和物位移服务的系统。该子系统主要包括行使人和物位移服务的载体，以及行使这些载体活动的人、财、物等子系统组成。一定的物流基础是该区域物流的物资位移服务的载体基础。

经济基础是人们利用资源在一定地域上进行物质资料生产、流通、分配和消费活动时价值创造的总和。一定的经济基础是该区域物流的物资位移服务的物质基础。

基础环境是人类周围一切物质、能量和信息的总称，即包括大气、水、土壤和生物等。也包括有人参与与组织的一些管理活动以及开展这些管理活动所具备的文化素养，意识形态，精神气质等等，这主要包括政府管理部门的管理服务水平，人们的市场意识、法律意识、规则意识等认识水平。

2 区域物流系统发展的负熵机理

区域物流系统是一个非平衡的开放系统，运用协同学的理论和方法可以研究区域物流系统内部的协同关系，即物流基础、经济基础、基础环境子系统发展的动态分析，从而使区域物流系统的各个子系统进一步转化为客观有序的状态。

在区域物流系统发展中，分别将物流基础系统定为Lg，经济基础系统为Ec，基础环境子系统En，因此从系统要素构成看，区域物流发展系统是物流基础、经济基础和基础环境三个子系统的组成的相互联系、相互依存的统一整体。

上述分析，物流基础子系统是区域物流发展的主体，经济基础子系统是区域物流发展的实物流主体，没有物流，经济基础创造的物质商品无法有效地送达需要的社会团体及个人手中，就无法有效满足人类物质生活的需要，而没有经济基础系统，区域物流的物质载体及物流基础系统就会变成无水之渠，而上面两个子系统的有效运行，必须有一个良好的柔顺的社会等外部环境为基础。因此一个区域物流的发展必须是在一个良好的基础环境下。物流基础子系统与经济基础子系统的协调、同步的协同性发展，区域物流中的每一个子系统都是多因素、多结构、多变量的系统，都包含着极具复杂的关联关系的要素，各构成要素以一定方式相互依存，相互制约，正是它们之间的相互作用决定着区域物流发展的过程和演进方向。随着时间的推移，各子系统会发生不断变化，向着更高一层的阶段演化，在各子系统的不断演化中，它们之间的相互作用强度也会跟着发生变化，这种作用机制的变化，可用行为矩阵来定量描述。

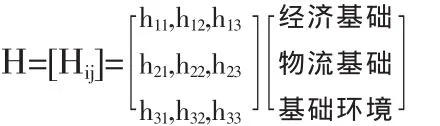
当i=j时，hij表示区域物流各子系统单位水平或投资下的状态和性质，当时，hij表示区域物流系统中j系统i子系统的影响系数，矩阵元素hij将随着时间的推移而变化。而在较短时间内，可将hij视为确定常数，通过对已有的区域的物流基础、经济基础及基础环境各系统的分析，采用一定的数学模型计算可获得。如果用列向量M表示在某一时刻t某一区域区域物流的行为活动水平，可以是深度、广度等。其分量m1，m2，m3，分别表示区域物流系统中，各子系统的发展和投资水平，它们体现该区域发展政策与发展条件，则B=H*M表示各子系统在发展政策干预下发展状态性质，M=[m1,m2,m3]T。

之前的分析，是基于系统内部各子系统之间的相互作用，相互联系的基础上。而区域物流协同发展系统是一个开放性系统，所以要将区域物流与外界联系起来进行分析。区域物流系统运行过程实质是物持、能量和信息的交互过程，即从外获取信息、技术、资金、能量并向外界提供产品及相关服务。这种物质、能量和信息的交换过程充分体现了区域物流的系统开放性。

熵的概念源于热力学，热力学第一定律描述了能量守恒与转换的定律，它的核心概念是能量的。热力学第二定律描述了自然广泛存在的不可逆现象。但是它缺少一个像能量这样的量度。为此，德国物理学家克劳修斯于1865年提出了热力学熵的概念。热力学熵类似能量，但又不同于能量，并认为熵和热一样，体现了系统内部的离散倾向。从热力学观点看，系统熵的变化ds与系统的温度T和热量变化dQ之间有如下关系：s=dQ/T。

然而，在这里对熵的理解仍然停留在宏观层次上，而且公式中描述的还中人是熵的变化，对熵的本质含义还有待于研究。

为了提示熵的本质，特别是它对应的微观状态，1872年物流学家玻尔兹曼提出了熵概述的统计解释：由于熵和玻尔兹曼积分微分议程中H函数只差一个符号，因此可以用它定量地描写热力学第二定律，而且在熵和系统微观状态数和对数之间存在一定的比例关系。这一关系由美国的吉布斯表述为：

S=Kblogw

Kb－为玻尔兹曼常数

W－为系统微观的状态数

显然可能的微观状态数越多，系统内微观粒子的状态分布也就越平均，或者说它们可以具有十分不同的运动状态，这从整体上看就表现为系统内部的十分混乱。可见，熵值的大小可以作系统内部混乱程度的标度。

1948年，申农和维纳提出的信息熵概念是对熵概念的一次最深刻的发展。按维纳的意见：熵是消息的负对数，它代表了系统与外界进行交换的东西。按申农的理解：熵是像坡尔兹曼H函数一样表征了消息不确定程度。因此，系统不确定性的减少就意味着它的确定性程度的增加，即组织程度的增加。信息熵的数学表示式为：

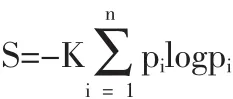
pi―表示状i出现的概率，当p=1时，S=0，系统只有一种状态；当p1=p2=…=pn=1/n时，系统熵值很大。

在通信中，系统因接受到了信息而减少或消除了它关于信息源的不确定性程度。因此，可以用信息熵的减少度作为得到信息的量度。

对于区域物流系统来说，熵也可视为其一种状态函数，是混乱无序的程度标志。熵增加意味着系统有序态的破坏，即系统朝着不协同方向发展。把握区域物流系统熵的变化，即可判明系统演替的方向及其进程。区域物流系统内部的熵产生是区域物流协同发展的障碍。

我们定义区域物流系统内的净熵的积累率ds/dt为系统协同发展的驱动力。如果ds/dt>0系统向退化方向发展，从有序走向无序，即不协同发展；如果ds/dt<0系统向进化方向发展，从无序走向有序，即协同发展。另设des/dt为环境输入系统的熵流入率，dgs/dt为系统的熵产生率，dos/dt为系统熵流出率。则[dos/dt-des/dt]为系统与环境的熵变换率。根据系统熵产出率和与环境熵交换率的平衡条件，可得：

ds/dt=dgs/dt-[dos/dt-des/dt]

由前述分析，要使区域物流系统驱向协同发展，即ds/dt<0

则dos/dt-des/dt>dgs/dt

又因系统产生的熵大于零，即则可得dgs/dt>0

dos/dt>des/dt

上式表明，要使区域物流系统驱向协同发展方向，必须使系统流出的熵大于流入的熵。即使系统获得负熵流，从而使系统的总熵下降，避免系统熵增加，导致系统出现无序状态。这就是区域物流发展的负熵机理。

3 区域物流的内部协同状态模型

从贝纳德、激光转变、Zhabotinsky花纹和化学波到生态党的宏观结构、社会经济系统的发展和变化，自组织现象普遍存在着[2,3]。自组织现象具有如下基本特征：

开放性：非平衡热力学证明了无离热平衡是发生非平衡相变的必要条件。只有从外界向系统注入能量和（或）物质，维持一定的能流和（或）物质流，系统才能维持平衡态。因此，实现非平衡相变的系统必须是开放的系统。

合作性：合作是一切相变的客观基础。不管非平衡相变合作行为深处的机制是什么，新相性质较之老相有显著的改变，没有众多子系统同步行动是无法产生的。

随机性：根据理论物理的基础定律，耗散的地方，就必在伴随着有涨落，使系统呈现随机性。

用(k1,k2…kn)表示系统的状态，k1是空间r和时间t的函数，并把n个状态变量作如下∂/∂tk=N(α,k,△,r,t)+F(t)的缩写：(k1,k2…kn)=k，则协同学将处理形如下的运动方程

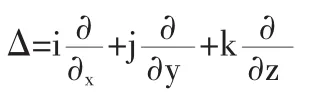
式中a表示控制参数，表示随机涨落，根据上述自组织现象的特征可知，子系统的运动议程必须是线性的、含可控参数的随机偏（或常）微分方程。议程的非线笥是系统合作性的唯一数学表达，而开放系统偏离随机态“距离”，则由议程中的外参数来调节，方程包含的涨落则是随机性的数学反映。

支配原理和序参量是协同学的又一重要概念。协同学处理自组织问题的程序大致分为三步，第一步，作线笥稳定性分析，确定稳定模和不稳定模；第二步，使用支配原理水运稳定模，建立序参量议程；第三步，解序参量方程，决定系统的宏观结构。

具体来说，首先将控制参数调到临界点，使系统线性失稳，这是系统性质发生急剧变化的前提。然后分析K中各分量深化的快慢，或K的各模式深化的快慢。如果快慢悬殊，就可以消去弛豫变量或快弛豫模式。得到一个或少数几个慢变量或慢变模式为序参量。

最后，必须在忽略涨落和考虑涨落的两种情形下求解序参量方程，以便得出物理结论，说明或预言自组织现象。

综上所述，自组织理论认为，系统运动状态的改变是由于系统内部非线性相互作用以及子系统的协同作用的结果，外部环境向系统输入物质和能量。对系统的相变提供了条件，并不能简单地作为控制作用，系统的有序不是来自外部，而是系统内部自发产生的。正如协同学原理所指出的，系统各部件（子系统）之间相互协调的结果，将使整个系统形成一个微观个体层次下不存在的新结构和特征。也就是说，可以在宏观层次上形成某种整体效应或通过自组织方式形成有序的宏观结构。

设xi（i=1,2…）为反映经济基础、物流基础的状态变量，由于各状态变量的单位不同，故对各状态变量进行无量纲化，设无量纲化后的序列为：相应的一阶累加生成序列，则的变化率依赖于：

（1）经济基础、物流基础的内协同效应，即其自身发展结果，记自发展项为

（2）经济基础、物流基础之间外协同效应，即经济基础、物流基础间的协同效应，记协同项为

（3）经济基础、物流基础发展过程中的灰色效应，该作用来源于经济基础、物流基础自身的抑制效应与各要素之间的竞争效应：本文统称为经济基础、物流基础发展过程中的灰色作用项为

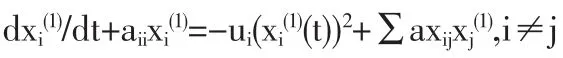
由于在由于在区域物流系统演化的两个临界点之间，涨落只是一种干扰，系统本身的稳定机制使涨落总是很容易被衰减，乃至消失，且建立区域物流系统状态模型的主要目的是找出规定区域物流系统有序程度的序参量，以便在实际工作中充分发挥序参量的作用，加强系统之间的协同效应，促使区域物流系统向更高的有序程度发展，而不是预测区域物流系统何时发生相变或跃迁，因此，本文在建立模型时忽略了涨落的作用。

模型的参数aii,aij,bi即是经济基础、物流基础之间协同与竞争作用大小的衡量，这些参数可以通过应用非线性微分方程色系统建模方法推导得出。通过分析此模型的状态方程组就可发现:状态程组哪些状态变量的弛豫系数为正.哪些状态变量的弛豫系数为负.通过绝热近似方法消去弛豫系数为负的状态变量，剩下的状态变量就是该系统的慢变量，即序参量。我们还可以采用数值计算方法即四阶龙格-库塔法得出此模型的数值解.然后应用绝热消去法消去系统的快变量，余下的慢变量就是该系统的序参量.由于方程组中是经过一阶累加生成和无量纲化后得到的，因此方程的数值解需要作还原处理，然后得到区域物流内物流基础与经济基础协同发展系统状态变量的模拟值.这可以对区域物流协同发展过程进行预测。

[1]喻传赞，彭匡鼎，张一方等.熵、信息与交叉科学[M].昆明：云南大学出版社，1994.

[2]郭治安，沈小峰.协同论[M].太原：山西经济出版社，1991.

[3]孟昭华.关于协同学理论和方法的哲学依据与社会应用的探讨[J].系统辩证学学报，1997,5(2).

F250

A

1002－6487（2011）07－0072-03

江苏省高校哲学社会科学研究基金项目（09SJD630072）

张中强（1973-），男，江苏沛县人，博士，副教授，研究方向：运营与物流管理。

（责任编辑/易永生）