基于非线性动力系统的我国CPI和PPI非线性关系研究
2011-11-01邓月明李兴绪
邓月明,李兴绪
(云南财经大学统计与数学学院,昆明650221)
基于非线性动力系统的我国CPI和PPI非线性关系研究
邓月明,李兴绪
(云南财经大学统计与数学学院,昆明650221)
文章根据我国2002年1月~2009年10月CPI和PPI的月度数据,应用非线性动力学的方法,建立了非线性动力系统(C-PNLDS)模型,来揭示我国CPI和PPI的非线性关系。结果表明:CPI具有自我增长机制,PPI对CPI有加速抑制的影响;PPI也具有自我增长机制,CPI自身对PPI的增长有抑制作用,但它的平方项加速了PPI的增长;耦合项对CPI无影响,而使PPI受损,所以二者是共栖(偏害)的关系。
CPI;PPI;非线性动力系统模型
0 引言
居民消费价格指数简称CPI,是度量一组代表性消费商品及服务价格水平随着时间而变动的相对数,反映居民家庭购买的消费品及服务价格水平的变动情况。生产者价格指数的简称PPI,在这里特指工业品出厂价格指数。工业品出厂价格指数是反映全部工业产品出厂价格总水平的变动趋势和程度的相对数[1]。
居民消费价格指数(CPI)和工业品出厂价格指数(PPI)有着各自的计算方法和用途,但二者之间又存在着密切的联系。分析清楚二者之间的关系,可以对我国的居民消费情况、工业品内部结构以及经济运行情况作出基本的判断,对宏观经济政策的制定起着重要的作用。
那么二者究竟是什么关系?是CPI变动带动PPI变动?还是PPI变动带动CPI变动?谁决定谁?很多专家学者可谓是见人见智,研究方法也有很多。
研究CPI与PPI关系的方法归结起来有线性回归分析、格兰杰因果检验、误差修正模型、协整检验和VAR(向量自回归)模型,这些方法揭示的都是CPI与PPI线性的关系,但是在复杂、现实的经济体系中,二者之间的关系很可能是非线性的。本文将选取我国2002年1月~2009年10月的CPI和PPI月度数据,用动态计量经济学的方法建立CPI和PPI的离散型非线性动态模型,再转化为CPI-PPI非线性动力系统(C-PNLDS)模型来分析CPI与PPI之间的非线性关系。
1 非线性动力系统(C-PN LDS)模型的建立
1.1 广义Lotka-Volterra模型介绍
Lotka-Volterra模型最早是由美国生态学家Lotka和意大利数学家Volterra为模拟一些生态现象而提出来并进行研究的,这个模型又称为捕食者被捕食者模型或弱肉强食模型。生物群体中的两个物种通过一定的相互作用进而形成的关系是最简单的动力学系统。两个物种之间的相互关系可能是相互独立,也可能是相互竞争,或者是相互促进。
罗纳德·肖恩[2]给出了广义Lotka-Volterra模型,这个模型的标准形式为:

在上述模型中a和b是一次变量反馈系数,如果a和b是正数,x和y回自然增长,反之则会自然下降;c和d是二次变量反馈系数,如果c和d是正数,则x和y回加速增长,反之则会发生阻塞现象;e和f是耦合项xy的系数。当模型(1)用于研究两个变量之间的关系时,根据e和f的符号,可以得出x和y的9种相互作用的关系(见表1)。
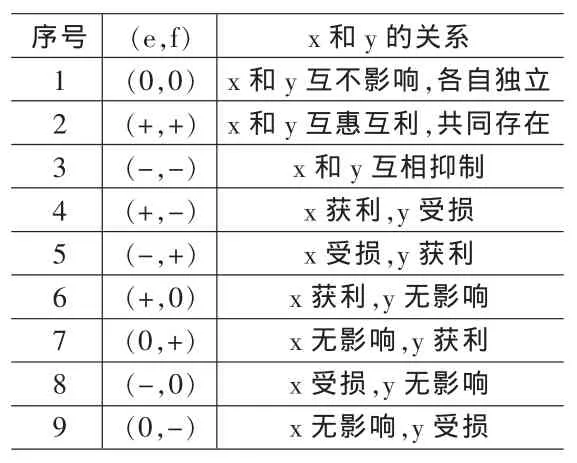
表1 两个变量相互作用的关系特征表
1.2 非线性动力系统(C-PNLDS)的基本假设
假设1系统性。C-PNLDS是在不考虑其他变量影响的情况下由CPI和PPI非线性相互作用而形成的具有一定结构和功能的整体。
假设2连续性。C-PNLDS是一个连续系统,CPI和PPI都是时间的连续函数。
假设3可差分性。本质上C-PNLDS是一个连续系统,然而直接建立并求解一个微分方程比较困难。所以把C-PNLDS作为一个离散的可差分系统,就可以根据统计数据建立差分方程组进行计算,再转化为微分方程组。
假设4确定性。C-PNLDS难免受到随机因素的干扰,但只要随机干扰因素是平稳的,就可以不考虑随机因素的影响,而只考虑C-PNLDS中的确定性关系。
1.3 非线性动力系统(C-PNLDS)模型
从模型(1)的表达形式可以明显的看出来,广义Lotka-Volterra模型,x和y的相互影响只是通过耦合项xy间接发生,但从实际情况来考虑CPI可能直接影响PPI的增长或减少,甚至是加速PPI的增长或减少;反过来PPI也可能直接影响CPI的增长或减少,甚至是加速CPI的增长或减少。同时,CPI和PPI具有明显的时间趋势,还可能有显性的时间变量。因此,把广义Lotka-Volterra模型进一步扩展为CPNLDS模型:
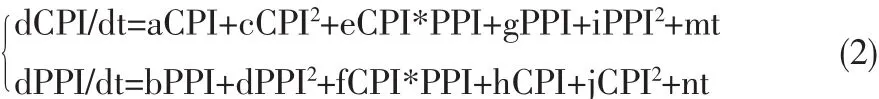
模型(2)为非线性动力系统。若m、n不显著,则为自治平面非线性动力系统,为CPI和PPI的最高幂次不超过二次的系统演化方程。a、b、c、d、e、f、g、h、i、j、m、n为系数,当系数取不同值时,C-PNLDS有以下几种特殊情况:
(1)e、f、g、h、i、j、m、n均为0,则表示CPI和PPI是两个独立发展的系统,具有自我演化的动力机制。当a、b大于0时则表示CPI、PPI两个系统自我增长;当a、b小于0时则表示CPI、PPI两个系统自我抑制;当c、d大于0时则表示CPI、PPI两个系统具有加速发展机制;当c、d小于0时则表示CPI、PPI两个系统具有减速发展机制,具有阻塞因素。
(2)如果g、h、i、j大于0,则CPI和PPI之间具有互助关系,其中i、j为加速度系数;如果g、h、i、j小于0,则CPI和PPI之间具有互抑关系,其中i、j为减速度系数。
(3)如果e、f大于0,表示CPI和PPI之间产生协同效应,CPI和PPI之间为互惠关系;如果e、f小于0,则表示CPI和PPI之间具有竞争关系;如果e、f一正一负,则表示CPI和PPI之间具有捕食关系;如果e、f有一个为0,则表示CPI和PPI之间具有共栖关系。
(4)如果c、d、e、f、i、j等于0,则C-PNLDS为非自治的线性系统,当m、n也等于0时,C-PNLDS为自治的线性系统,其实就是一阶循环式结构模型。
(5)如果a、b大于1,且e、f、g、h、i、j、m、n大于0,则CPI和PPI互为因果关系,相互促进,产生协演化。这是一种最理想的关系。
在这里直接估计模型(2)是很困难的,因为模型(2)中的方程是非线性的微分方程,其中平方项和耦合项是强非线性项,难于确定函数关系。所以,在这里我们采用的是对离散的非线性差分模型的参数进行估计,模型的形式为:

在模型(3)建立好之后,我们要对其进行参数估计,并对u1、u2进行EG平稳性检验,如果通过了检验,则表明模型(3)中的变量之间存在协整关系。并且在可决系数很高的情况下,模型(3)可以近似的转化为C-PNLDS模型,即模型(2)。这样我们通过对模型(3)的参数进行估计,进而得到模型(2)的参数。
2 实证分析
本文选取我国2002年1月~2009年10月的CPI和PPI月度时间序列数据,对模型(3)用OLS进行估计参数,得到表2和表3的结果。
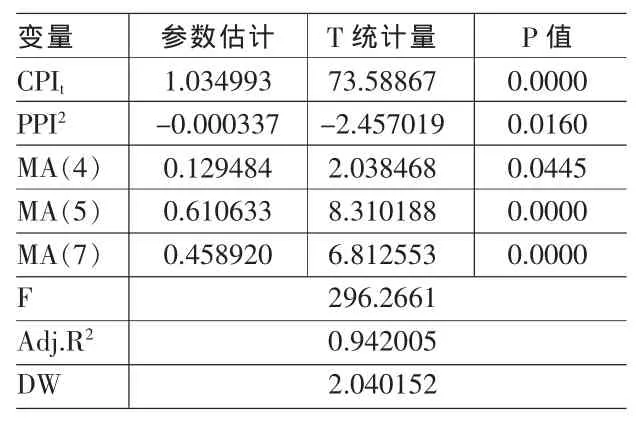
表2 模型(3)第一个方程即CPIt+1参数估计结果
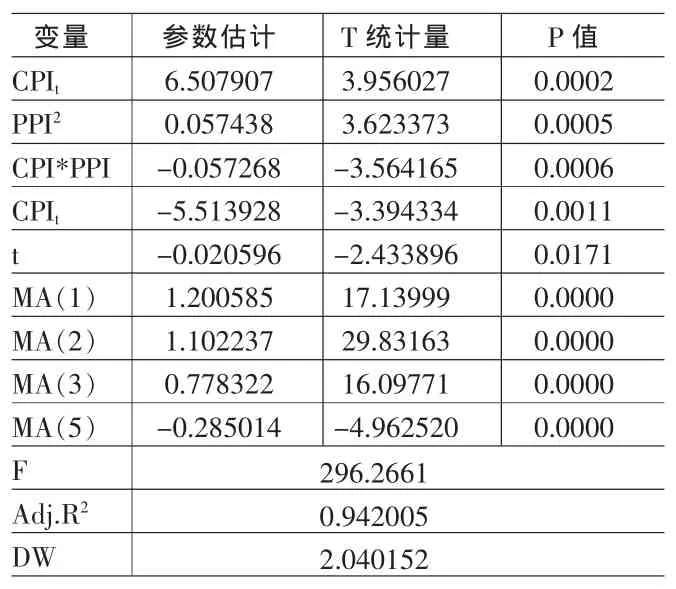
表3 模型(3)第二个方程即PPIt+1参数估计结果
从表2和表3中可以看出,两个方程的F值和每个变量的T值都在5%的水平下显著,调整后的很高,所以模型有很好的解释能力。由于CPI和PPI是时间序列变量,很可能是非平稳变量,变量之间是否存在协整关系对C-PNLDS模型非常重要,所以还要用EG两步法对其进行协整检验,检验结果见表4和表5。

表4 序列平稳性检验表
从表中的检验结果可以看出CPI和PPI两个变量在没有差分时T统计量的值均大于5%显著水平下MacKinnon临界值,说明这两个是非平稳变量,而在一阶差分后T统计量的值均小于5%显著水平下MacKinnon临界值,说明是平稳的。其残差、T统计量的值均小于5%显著水平下MacKinnon临界值,说明u1、u2也是平稳的,所以模型变量之间具有协整性,即存在长期的稳定关系。
因此,可以由模型(3)可以近似的转化为模型(2),最终得到的C-PNLDS模型为:

模型中有3个非线性项,而且第二个方程时间变量在5%的水平下是显著的,所以该系统为非自治非线性动力系统。这两个方程具有明显不同的增长机制,CPI方程包含一个一阶正反馈,表示方程有自我增长机制;还包含一个二阶交互项,且系数是负的,表明PPI对CPI有加速抑制的作用。PPI方程包含一个一阶正反馈项,表明方程具有自我增长机制;方程又包含一个负的耦合项,表明耦合项(CPI与PPI的乘积项)对PPI有不利的影响,CPI和PPI是共栖偏害的关系;CPI的系数是负的,表明CPI对PPI有抑制作用;方程中还包含一个二阶交互项(CPI的平方项),且系数是负的,表明CPI对PPI有加速抑制的作用。
3 结果分析
CPI与PPI之间呈现的上述这种非线性的关系似乎有悖常理,但是结合内容构成和现实经济的运行状况进行分析就会看得很清楚。
CPI的调查内容分别为食品、烟酒及用品、衣着、家庭设备用品及服务、医疗保健及个人用品、交通和通信、娱乐教育文化用品及服务、居住等八大类。其权重分别为34%、4%、9%、6%、10%、10%、14%、13%,其中工业消费品的权重大约占了一半,而另一半是食品和服务项目。PPI的调查内容分为生产资料和生活资料,大部分的调查内容是原材料、电子、化工等生产资料,大约占2/3,而用于居民最终消费的生活资料只占1/3。所以,消费品价格上涨对CPI的影响大过对PPI的影响,原材料价格的上涨对PPI的影响大过对CPI的影响。
结合现实的经济情况来看,从2007后半年开始到2008年8月由于原油、煤炭等自然资源的匮乏,导致原材料价格的大幅度上涨并直接推动PPI飞涨,最高在2008年8月达到110.1。而从2007后半年到2008年2月CPI大幅上涨,最高达到108.7,其原因是在此期间以猪肉为代表的食品类产品价格迅速大幅上涨带动的。而在国家相关政策和市场机制自我调节的作用下,食品价格逐渐得到了有效的控制。并且2008年我国出口量大幅减少,造成了产能过剩,国内供给增加,加快了物价下降,进而使CPI下降。上述原因使得CPI从2008年2月开始呈逐渐下降态势。所以,从2008年2月到2008年8月CPI是逐渐下降的,而PPI是上涨的,类似CPI与PPI倒挂的现象在2004年后半年也有出现,这里就不做详细的分析。
可见,由于二者构成不同,食品价格得到控制逐渐下降,产能过剩导致物价下降,使得CPI逐渐下降;而原材料价格飞涨推动PPI快速上涨,进而导致了二者出现了倒挂的现象,这种现象进而导致了PPI对CPI有加速抑制的作用、CPI对PPI有抑制作用及二者是共栖偏害的关系,即模型(4)中第一个方程中PPI平方项的系数和第二个方程中CPI和CPI*PPI的系数是负的。
4 与VAR模型的比较
现有的对CPI和PPI关系研究的主要方法是向量自回归模型,即VAR模型。但是VAR模型揭示的只是CPI和PPI两者之间的线性关系。本文不对VAR模型的建模过程进行详细阐述,只对比VAR模型和C-PNLDS模型的结果,进而可以比较出这两种模型在揭示CPI和PPI关系上的优劣。
从表4的结果中可以看出,C-PNLDS模型得出的CPI和PPI调整后的R2都比VAR模型得出的R2要高,这说明C-PNLDS模型比VAR模型的解释效果要好;而且C-PNLDS模型得出的CPI和PPI的AIC值都要比VAR模型得出的AIC值要小,这也说明用C-PNLDS模型来分析揭示CPI和PPI的关系比VAR模型的效果要好。
5 结论
从以上分析,我们可以得出:整个C-PNLDS模型为非自治非线性动力系统;CPI具有自我增长机制,PPI对CPI有加速抑制的影响,即PPI的平方项对CPI有负的影响;PPI也具有自我增长机制,CPI自身对PPI的增长有抑制作用,但它的平方项加速了PPI的增长,耦合项对CPI无影响,而使PPI受损,所以二者是共栖(偏害)的关系。
CPI和PPI是我国宏观经济的两个重要指标,对宏观经济政策的制定有着重要的作用,本文运用非线性动力系统,建立了C-PNLDS模型,揭示了二者之间的非线性关系,希望能对各位学者更清楚地认识和更深入地研究二者之间的关系有所帮助。

表5 参差平稳性检验表
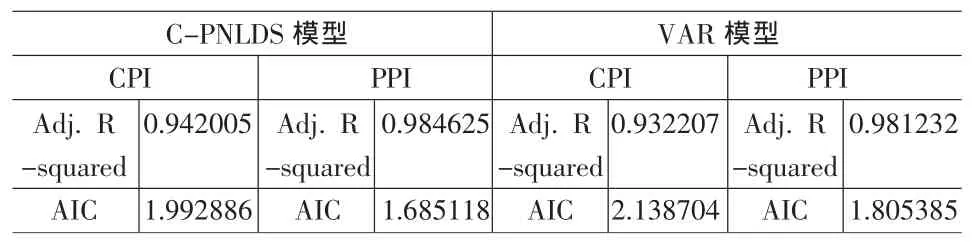
表6 C-PNLDS模型和VAR模型主要参数值对比
[1]徐国祥.统计指数理论及应用[M].北京:中国统计出版社,2004.
[2]罗纳德·肖恩.动态经济学[M].北京:中国人民大学出版社,2003.
[3]赵国庆.寻求我国GDP对FDI的最优依存度与FDI最优规模—基于1980~2003年我国GDP与FDI非线性动力系统的研究[J].管理世界,2006,(1).
[4]刘文华.正确看待PPI和CPI的差异[J].中国统计,2005,(7).
F222.1
A
1002-6487(2011)07-0030-03
邓月明(1985-),男,吉林长岭人,硕士研究生,研究方向:统计学方法与应用。李兴绪(1967-),男,云南昆明人,博士,教授,研究方向:统计学方法与应用。
(责任编辑/亦民)
