高压并联电抗器非线性模型的分析①

岳 昊， 徐永海， 刘颖英， 朱永强， 肖湘宁

(华北电力大学电气与电子工程学院， 北京 102206)

高压并联电抗器非线性模型的分析①

岳 昊， 徐永海， 刘颖英， 朱永强， 肖湘宁

(华北电力大学电气与电子工程学院， 北京 102206)

建立精确的高压并联电抗器非线性模型是对超(特)交流输电系统进行各种仿真分析的基础。基于单相并联电抗器的电磁关系，充分考虑铁心非线性的影响，提出了一种适用于谐波分析、易于仿真实现的单相并联电抗器的非线性模型，它由反映其磁化特性的非线性电感与反映其铁心损耗的非线性电阻并联再与漏阻抗串联组成，并且分别引入ir-u和i1-u瞬时特性曲线来求解非线性电感和非线性电阻。结合我国晋东南-南阳-荆门1 000 kV特高压交流输电试验示范工程中的高抗参数在PSCAD/EMTDC中进行了建模和仿真，证明所建立的模型能够比较准确地反映高抗的非线性特性，为进行超(特)高压交流输电系统仿真模型的搭建和对其进行谐波特性分析提供了必要条件。

高压并联电抗器； 非线性模型； 特高压； 仿真

由于我国西电东送和南北互供等远距离送电的要求，相当一部分超(特)高压线路都比较长，单段线路的充电功率很大，必须使用高压并联电抗器(简称高抗)进行补偿[1]。它不仅可以补偿长线电容效应，提高功率因数而改善供电质量、限制电压升高而保护设备，而且可以减少线路损耗并维持无功平衡[2]。

因为铁心含有气隙的缘故，高抗的饱和程度低于变压器，其谐波含有率低但其谐波含量却很高[3]。尤其当夜间低谷负荷时，线路电压偏高，高抗可能工作于饱和区。研究[4]表明，在运行电压较高或在工频过电压情况下，高抗三次谐波电流含量有较大幅度的增加。因此在对超(特)高压交流输电系统进行各种仿真分析时，不能忽略高抗的饱和特性，而需要建立高抗的非线性模型。

以往，人们对常规高压并联电抗器模型的研究较少，在已有的研究中，文献[5]在已知B-H磁化曲线和平均磁路长度的条件下推导出了由线性电感并联受控电流源的非线性电抗器的模型，但这种模型对于原始数据的要求较苛刻，需要电抗器的B-H磁化曲线及其尺寸，而且在模型中没有考虑铁心损耗带来的非线性。文献[6]定性地给出了空心电抗器的模型，即由气隙电感和铁心电感并联再与漏电感串联，但该模型同样没有考虑铁心损耗，而且并没有对起关键作用的铁心电感如何实现进行描述。

本文在推导高抗电磁方程的基础上，建立了高抗比较精确的非线性模型，即由表示其磁化特性的非线性电感与表示其铁心损耗的非线性电阻并联再与漏阻抗串联。本文引入i-u瞬时特性曲线来反映对应于铁心磁化特性的电感的非线性(无功特性)；引入瞬时特性曲线来反映对应于铁心损耗的电阻的非线性(有功特性)。结合我国晋东南-南阳-荆门特高压交流试验示范工程中高抗的实际参数在PSCAD/EMTDC电磁仿真软件中建立了高抗和特高压系统的仿真模型，并对高抗的特性进行了分析。

1 高压并联电抗器数学模型的推导

图1(a)为电抗器结构示意，电抗器由一个主铁心柱和两个等截面等长度的旁轭组成。旁轭面积大于主铁心面积。主铁心上绕有匝数为N的线圈。铁心为分段式，段间间隙用非磁性绝缘材料构成。由此可以看出它相当于只有原边绕组的变压器，因此本文在建立电抗器模型的过程中将文献[7～10]中使用变压器空载试验数据求解变压器铁心激磁阻抗的方法引入到求解高抗铁心激磁阻抗中来，此时需要的数据为电抗器常规试验数据。

图1 单相并联电抗器的物理模型

图1(b)为单相并联电抗器的物理模型，u为外加的正弦电压，im为激磁电流，φ1为经过铁心的主磁通，φ2为经过旁轭的磁通，φσ为铁心与空气交链的漏磁通，e为线圈感应的电动势。

建立相应的电路与磁路方程为

φ=φ1+φσ

(1)

Ψ=Nφ=N(φ1+φσ)

(2)

由磁路欧姆定律φ=FΛ=Ni1Λ并代入式(2)得

Ψ=N(Ni1Λ1+Ni1Λσ)=(L1+Lσ)i1

(3)

(4)

再由式(3)得

(5)

如果考虑铁心损耗，则激磁电流im包括磁化电流i1和铁耗电流ir，即

im=ir+i1

(6)

其中

(7)

式(1)和式(2)为电抗器的磁路方程，式(5)～式(7)为电路方程，式(3)和式(4)为电磁接口方程。各式中：φ为通电线圈产生的总磁通，包括主磁通φ1和漏磁通φσ；Ψ为总磁通φ交链N匝线圈的磁链；im为激磁电流；ir为产生铁耗的等效电流；i1为产生磁场的等效磁化电流；Λ和Λσ分别为主磁通路径和漏磁通路径的磁导；L1和Lσ分别为主电感(非线性)和漏电感(常数)；r为线圈电阻；rFe为铁耗等效电阻；将Zm=rFe//jωL1称为电抗器的激磁阻抗，将

Zσ=r+jωLσ

(8)

称为电抗器的漏阻抗。

根据式(5)～式(7)可得单相并联电抗器的等效电路如图2所示。由于电抗器的铁心是分段式带间隙的，因此主磁通通过铁心和间隙闭合。又因为气隙的磁导率恒定，非线性电感L1又可等效为线性的气隙电感Lgap和非线性的铁心电感Lnon。

为了准确建立高抗的非线性模型，根据文献[8～11]，引入ir-u瞬时特性曲线表示铁耗等效电阻rFe，引入i1-Ψ瞬时特性曲线表示激磁电抗，即

L1=Lgap+Lnon

(9)

rFe和L1的计算式为

ir=f1(u)

(10)

(11)

i1=f2(Ψ)=f3(u)

(12)

(13)

式中，f1(u)、f2(Ψ)为对ir-u、i1-Ψ曲线进行适当的数值模拟得到的函数；忽略漏阻抗时，e=u；由于Ψ与u在数量上是线性关系(系数为角频率ω)，只是相位相差90°，因此为了计算方便可以直接求取i1-u的数值关系f3(u)。由式(11)和式(13)可见，最终求得的rFe和L1均为外加电压u的瞬时值的函数。

图2 单相并联电抗器等效电路

求解模型参数需要提供的数据有：绕组电阻r、漏电感Lσ、ir-u和i1-u瞬时特性曲线。r和Lσ可由电抗器厂家提供的参数直接得到，ir-u和i1-u瞬时特性曲线可由电抗器的常规试验数据(Urms1，Irms1，P1)、(Urms2，Irms2，P2)、…、(Urmsn，Irmsn，Pn)经已编制的算法程序计算得到。Urms、Irms为电抗器试验电压、电流有效值，P为电抗器损耗值。

图2中的电抗器模型，将激磁电流分为用于产生磁场的无功电流和用于产生铁耗的有功电流，物理概念清晰，易于理解。激磁阻抗不但包括通常不可忽略的反映铁心饱和特性的非线性电感，同时也考虑了反映铁耗的非线性电阻，对于分析电抗器的非线性特性更为精确。在求解激磁阻抗的过程中，只需提供一组电抗器的试验数据，较之需要获取B-H曲线或Ψ-i曲线的方法要更容易。

上述电抗器的非线性模型在仿真中也易于实现，在PSCAD/EMTDC电磁暂态仿真软件中，使用可输入变量名例如“R”和“L”的可变电阻和电感元件作为非线性电阻和非线性电感，“R”和“L”为随着某一自变量变化的有具体数值的因变量，通过上述分析可知该模型使用的这一自变量为外加电压瞬时值。使用这样的可变元件的好处在于只需输入变量值就可体现电感的特性，免去了使用复杂的微分方程来模拟电感元件带来的麻烦。

2 单相高压并联电抗器激磁阻抗的计算

通过以上分析可知，建立电抗器模型过程中不能直接得到的参数是非线性电阻和非线性电感，即激磁阻抗。求解它的第一步是需根据电抗器的常规试验数据计算得到两条瞬时特性曲线，然后对曲线进行适当的数值模拟，最后得到激磁阻抗表达式。

2.1 瞬时特性曲线的计算

步骤1程序初始化。

(1)输入原始数据Urms(1×n)，Irms(1×n)，P(1×n)。

(2)计算Urms(k)的最大值U(k)的公式为

(14)

其中k=1，2，…，n。

(3)形成α(n×n)矩阵，其中

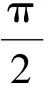
(15)

(16)

步骤2计算Ir(k)，其中k=1，2，…，n。

(17)

(2)迭代计算其余非线性段的Ir(k)，k=2，…，n。

步骤3计算Irms(k)和I1rms(k)，其中k=1，2，…，n。

(1)迭代计算Ir(k)对应的有效值Irms(k)

(2)计算I1rms(k)的公式为

(18)

步骤4计算I1rms(k)对应的最大值I1(k)。

(19)

(2)迭代计算其余非线性段的I1(k)。

步骤5输出结果U(1×n)，I1(1×n)，Ir(1×n)。

由Uk、Irk、I1k便可得到ir-u和i1-u瞬时特性曲线。

其中，Urms(1×n)、Irms(1×n)、P(1×n)分别为进行电抗器试验时的电压、电流有效值和损耗值。

2.2 瞬时特性曲线的数值模拟

为了得到如式(11)和式(13)所示的组成激磁阻抗的非线性电阻rFe和非线性电感L1，在计算出ir-u和i1-u瞬时特性曲线后需要对其进行数值模拟得到如式(10)和式(12)所示的表达式。

对于ir-u、i1-u的曲线数值模拟方法可以采用插值法或函数拟合法。插值法常用的函数为三次样条分段插值和分段线性插值。拟合函数可以使用最小二乘法的奇次多项式[12,13]，即

p=a1x+a3x3+…+a2n+1x2n+1

(20)

幂函数[5]为

y=ax+bxc

(21)

以南阳站高抗的i1-u瞬时特性曲线的数值模拟为例，当采用奇次多项式进行拟合时，由于求出的系数a2n+1可能为负，因此很难保证拟合函数的单调上升，有时会出现振荡现象，误差较大。如若采用三次样条插值，在线性段可以很好地与原数据曲线逼近，但分段较多，如图3所示，三次样条插值函数一共分了10段，即用10个3次多项式来表达这条曲线，增加了表达式的复杂程度，而且可以看到，插值曲线在拐点附近与原数据曲线误差较大。若减少三次样条插值函数分段数，则曲线的线性度将大大降低，每段都会出现波动。若采用幂函数拟合，虽然拟合表达式简单，但在拐点附近的误差较大，如图4所示。

图3 i1-u曲线三次样条插值结果

因为在上文提出的模型中，求解rFe和L1的过程并没有涉及到求导计算，所以可以使用分段线性插值，结果如图5所示。这样做的好处是，既可以很好模拟原数据曲线，又减少了分段表达式的个数(只用3个)而且表达式简单，易于写入程序进行仿真。

图4 i1-u曲线幂函数拟合结果(局部)

图5 i1-u曲线分段线性插值结果

在求得rFe和L1的表达式的基础上，笔者在PSCAD/EMTDC中，使用Fortran语言编制了一个输入变量为电抗器瞬时励磁电压，输出变量为电阻值和电感值的名为“受控非线性电阻(感)”模块，以实现rFe和L1的分段计算，并对模型中的可变电阻和可变电感进行控制。

3 算例分析

3.1特高压交流试验示范工程高抗的非线性仿真模型

本文采用我国1 000 kV晋东南-南阳-荆门特高压交流试验示范工程中单相高抗的实际参数建立了其仿真模型，并进行了非线性特性仿真分析。示范工程中在晋东南、南阳、荆门三站分别配置了高压并联电抗器。由于三站高抗的模型建立过程类似，因此下面仅给出南阳站高抗模型的建立过程。表1～表2为南阳站单相高抗的主要参数和试验数据。其中，Un、In、Zn、Sn分别为南阳站单相高抗的额定电压、额定电流、额定阻抗、额定容量。Up、Irms、Pt、Ps分别为高抗试验时的电压百分数、电流有效值、总损耗、杂散损耗。

将该组试验数据输入至第3.1节中所述的瞬时特性曲线计算程序中，得到i1-u和ir-u瞬时特性曲线如图6所示，并且使用第3.2节中的分段线性插值方法得到i1-u曲线函数为

(22)

式中：i1单位为kA，u单位为kV。

表1 南阳开关站单相高抗的主要参数

表2 南阳开关站单相高抗的试验数据

图6 南阳站高抗i1-u和ir-u瞬时特性曲线

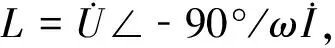
由于ir-u基本为线性，故可使用线性拟合，拟合式为ir=9.984×10-7u，等值电阻值为1.001 6×166Ω。

由于缺少漏阻抗参数，因此忽略漏阻抗，最终建立的南阳站单相高抗仿真模型，如图7所示。

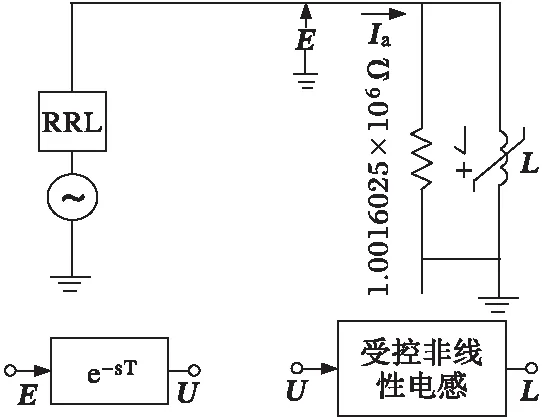
图7 南阳开关站单相高抗仿真模型

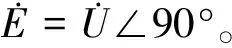
3.2特高压交流试验示范工程高抗特性仿真分析

3.2.1 高抗的非线性特性

由图8可以看出，当外加额定电压时，高抗电流畸变程度不大，为正弦波形；当外加1.5倍额定电压时(已经入饱和区)，电流为尖顶波，其中除了基波分量外，还含有一系列奇次谐波，其中以三次谐波为主。由于模型中使用了随电压变化的可变电感，因此当高抗电压高于拐点电压时，感抗瞬时值是周期变化的，即当电压瞬时值低于拐点电压时，感抗值为高抗的额定值，当高于拐点电压时，感抗值随电压升高而减小。

3.2.2 高抗接入特高压交流系统的仿真分析

本文以1 000 kV晋东南-南阳-荆门特高压交流试验示范工程为背景，采用国际上广泛使用的电磁暂态仿真软件PSCAD/EMTDC建立了特高压系统详细的仿真模型[14]。

在高抗全投的情况下，通过仿真得到晋-南线吸收容性无功功率约为1 191.5 Mvar，平均100 km的充电功率约为328.24 Mvar。荆-南线吸收容性无功功率约为899.9 Mvar，平均每100 km的充电功率约为309.24 Mvar，晋-南-荆线总平均每100 km的充电功率约为319.79 Mvar。

图8 南阳站高抗电流波形及感抗值的变化

表3为高抗不同投切状况下，线路上三站1 000母线的电压升高情况。可见线路高抗切除后三站电压都有所升高，当高抗全切后三站线电压都高于线路允许最高电压1 100 kV，晋东南、荆门站电压较高抗全投时升高约1.15倍，南阳站电压升高最严重，约1.21倍。而且可以看出，增设开关站并且投入高抗可以明显抑制由线路充电效应引起的过电压。

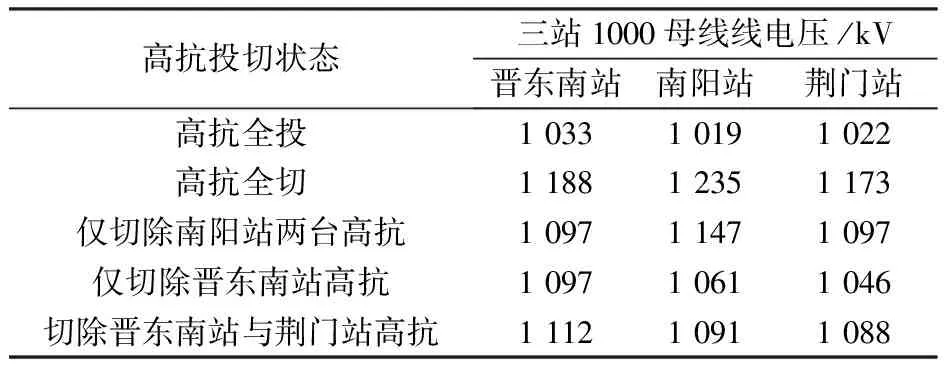
表3 线路高抗不同投切状况下三站线电压的比较

4 结语

在分析了并联电抗器电磁关系基础上建立的由非线性电感和非线性电阻并联表示的并联电抗器的模型，其计算过程简单、物理概念清晰、易于仿真实现。仿真分析表明，在1.4倍额定电压以下，高抗主要谐波电流含有率(HRI)极低，均在0.1%以下，表明高抗在正常电压工作时的线性度很好。以我国特高压输电系统为例的仿真表明，线路接入并联高抗后，降低了工频电压升高。

[1] 刘振亚．特高压电网[M].北京：中国经济出版社，2005.

[2] 刘孝为，陈楚羽，王宏(Liu Xiaowei，Chen Chuyu，Wang Hong)．超高压并联电抗器的结构特点和运行情况综述(Probe into the structure character & operation of EHV shunt reactor)[J].陕西电力(Northwest China Electric Power)，2006，34(5)：39-43．

[3] Li Shusen，Chen Xiaoyan， Zhao Zhengjun,etal.The study of 500 kV system harmonics in Central China power network[C]∥8th International Conference on Harmonics and Quality of Power，Athens，Greece: 1998．

[4] 冯宝忆(Feng Baoyi).华东500 kV电网谐波问题初探(Investigation on harmonics in ECPN 500 kV power network)[J].华东电力(East China Electric Power)，1992，20(4)：1-6．

[5] 赵宇红，王松江，王凤仁(Zhao Yuhong，Wang Songjiang，Wang Fengren)．非线性电抗器的数学模型与等效电路(Mathematic model and equivalent circuit of nonlinear reactors)[J].哈尔滨电工学院学报(HIET Journal)，1996，19(3)：307-313．

[6] Alexander G W，Hopkinson R H，Welch A U．Design and application of EHV shunt reactors[J].IEEE Trans on Power Apparatus and Systems，1966，85(12)：1247-1258．

[7] Prusty S，Rao M.A direct piecewise linearized approach to convert RMS saturation characteristic to instantaneous saturation curve[J].IEEE Trans on Magnetics，1980，16(1)：156-160．

[8] Neves W L A，Dommel H W．On modeling iron core nonlinearities[J].IEEE Trans on Power Systems，1993，8(2)：417-422．

[9] Wiechowski W，Bak-Jensen B，Bak Claus Leth，etal.Transformer core nonlinearities modeled in harmonic domain[C]∥Power Engineering Society Transmission and Distribution Conference，Dalian， China: 2005．

[10]Hosseinian S H，Vahidi B．Transformer no-load current wave shape considering core loss[C]∥IEEE Region 10 Annual International Conference，Taipei，China: 2007．

[11]Baghzouz Y，Gong X D．Voltage-dependent model for teaching transformer core nonlinearity[J].IEEE Trans on Power Systems，1993，8(2)：746-752．

[12]吴笃贵，徐政(Wu Dugui，Xu Zheng).电力变压器有源谐波模型(Active harmonic model of power transformer)[J].电网技术(Power System Technology)，1999，23(3)：34-37．

[13]张诚，廖勇，刘刃，等(Zhang Cheng，Liao Yong，Liu Ren，etal).一种考虑饱和的变压器仿真模型的分析(The analysis of the transformers saturation model)[J].重庆大学学报:自然科学版(Journal of Chongqing University：Natural Science Edition)，2003，26(10)：63-66．

[14]华北电力大学, 国网电力科学研究院.特高压系统谐波特性分析及潜供电流对重合闸的影响研[R].北京：华北电力大学；武汉：国网电力科学研究院，2009．

[15]殷幼军, 陆继明, 毛承雄，等(Yin Youjun，Lu Jiming，Mao Chengxiong，etal).单磁芯饱和电抗器的建模与仿真(Modeling and simulation of saturable reactor with single core using MATLAB)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)2006, 18(4) : 9-13.

AnalysisofNonlinearModelofHVShuntReactor

YUE Hao， XU Yong-hai， LIU Ying-ying， ZHU Yong-qiang， XIAO Xiang-ning

(School of Electrical and Electronic Engineering， North China Electric Power University， Beijing 102206， China)

Modeling of accurate nonlinear high voltage(HV) shunt reactor is basis of simulation analysis of EHV(UHV) AC transmission system. Based on the electromagnetic relations of single-phase shunt reactor and the effect of iron core nonlinearity, a new model of single-phase shunt reactor is presented for harmonic analysis and computer simulation. The shunt reactor is composed by a simple equivalent circuit consisting of an impedance representing the leakage flux losses in series with a parallel combination of a nonlinear inductance (accounting for the saturation of the iron core) and a nonlinear resistance(accounting for the iron loss). The nonlinear impedance is calculated by their-uandi1-ucurves which have been used for modeling of transformer excitation impedance. The results of simulation in PSCAD/EMTDC using the parameters of shunt reactor in China's UHV AC Pilot Project have proved that this model accurately reflects the nonlinear characteristics of shunt reactor, which is the prerequisite to complete the simulating model of EHV(UHV) AC transmission system and analyze the harmonic characteristic of the system.

high voltage(HV) shunt reactor； nonlinear model； ultra high voltage； simulation

2009-10-26

2009-12-11

国家电网公司特高压输电可行性研究项目(SGTGY2008609)；高等学校学科创新引智计划(“111”计划)(B08013)

TM472

A

1003-8930(2011)01-0039-07

岳 昊(1985-)，男，博士研究生，研究方向为电能质量分析与控制。Email:yuehome@163.com 徐永海(1966-)，男，博士，教授，主要从事电力系统谐波、电能质量等方面的教学及研究工作。Email:yonghaixu@263.net 刘颖英(1981-)，女，博士研究生，研究方向为电能质量分析与控制。Email:Liuyy1104@163.com 朱永强(1975-)，男，博士，讲师，主要从事电能质量、新能源等方面的教学与研究工作。Email:zyq@ncepu.edu.cn 肖湘宁(1953-)，男，教授，博士生导师，主要从事电力系统谐波、电能质量、现代电力电子技术应用等方面的教学与科研工作。Email:xxn@ncepu.edu.cn