消除偶次谐波的三电平NPC逆变器调制方法①

刘 斌， 薛毓强

(福州大学电气工程与自动化学院， 福州 350108)

消除偶次谐波的三电平NPC逆变器调制方法①

刘 斌， 薛毓强

(福州大学电气工程与自动化学院， 福州 350108)

针对传统空间矢量脉宽调制(SVPWM)方法的矢量选取方案使得二极管箝位型(NPC)三电平逆变器输出电压产生偶次谐波的缺陷，提出了一种能消除偶次谐波的改进型矢量选取方案。该方案在分析传统SVPWM产生偶次谐波机理的基础上，通过改进SVPWM中各矢量的作用顺序，使得逆变器输出电压半波奇对称，从而达到消除偶次谐波、抑制中点电压漂移的目的。同时，为避免进行复杂的三角运算，采用了基于60°坐标系的SVPWM方法以利于实时控制。仿真证明了上述方案的有效性。

偶次谐波消除； 二极管箝位型三电平逆变器； 矢量选取； 空间矢量调制； 半波奇对称

在二极管箝位型NPC(neutral point clamped)三电平逆变器中，电容电压不平衡是其固有的缺陷，它使输出电压波形发生畸变，甚至危及逆变器稳定运行；然而，传统电压空间矢量调制法SVPWM(space vector pulse width modulation)的冗余矢量选取方案会使得逆变器输出电压产生偶次谐波；偶次谐波的存在会引起中点电位的漂移和不稳定。在非线性负载条件下，当调制系数大于0.8时，极小的偶次谐波(尤其是2、4次谐波)都有可能引起中点电位漂移[1]；因此，必须对偶次谐波加以抑制。

针对谐波消去方法，目前采用最多的是基于解非线性方程组的特定谐波消去法[2，3]；该方法能有效地消除特定谐波，但消除谐波次数不能太多，否则计算量极大，不利于在线计算。鉴于此，本文在最近三矢量调制[4]下，遵循开关次数少、电压跳变小的原则，通过改进SVPWM中各矢量的作用顺序，使得逆变器输出电压半波奇对称，从而达到消除偶次谐波、抑制中点电压漂移的目的。同时，为避免在计算矢量作用时间时进行复杂的三角函数运算，本文采用了基于60°坐标系的SVPWM算法以利于实时控制[5]。

1 NPC逆变器的空间电压矢量模型

二极管箝位型三电平逆变器主电路拓扑如图1所示，电路工作时逆变器每相桥臂输出具有三种电平：Ud/2、0、-Ud/2，分别定义为P、O、N电平。三相桥臂对应33=27种输出电压状态，这27种状态在空间矢量平面上对应一个离散的点集，如图2(a)所示。

图1 三电平NPC逆变器拓扑

图2(a)中清晰地显示出27个电压矢量状态，占据19个空间位置，并且由坐标原点向外，空间电压矢量的冗余度依次递减。按矢量的模长可将矢量分为大矢量、中矢量、小矢量和零矢量；小矢量又可分为正小矢量和负小矢量，如表1所示。

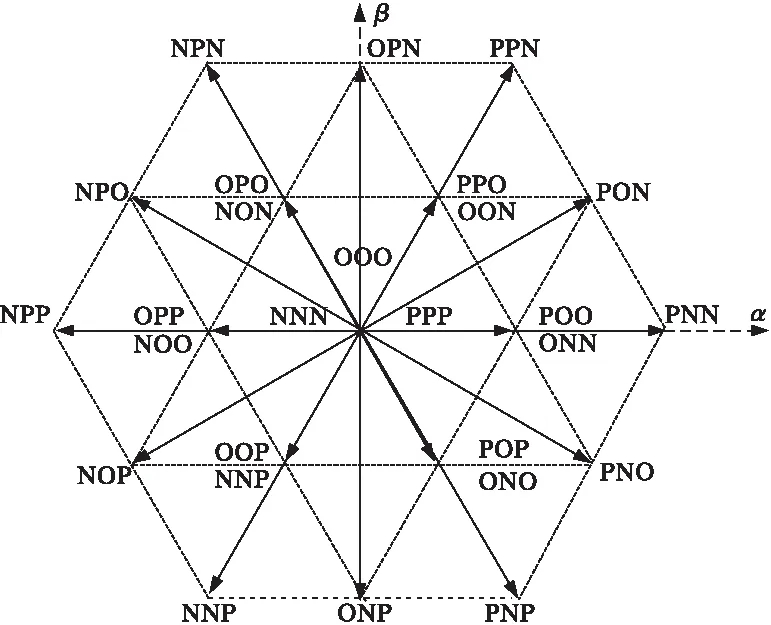
(a) 直角坐标系矢量图

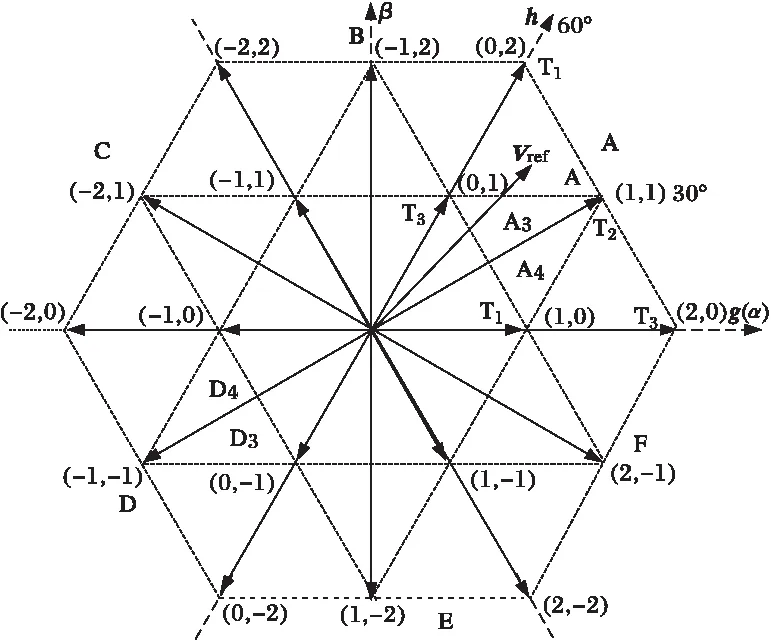
(b) 60°坐标系矢量图

矢量类型电压矢量模长冗余度空间位置 大矢量PNN，PPN，NPN，NPP，NNP，PNP23Ud1外正六边形顶点 中矢量PON，OPN，NPO，NOP，ONP，PNO33Ud1外正六边形每边中点小矢量正小矢量POO，PPO，OPO，OPP，OOP，POP负小矢量ONN，OON，NON，NOO，NNO，ONO13Ud2内正六边形顶点 零矢量PPP，OOO，NNN03坐标原点

2 基于60°坐标系的SVPWM算法

用60°坐标系为g-h坐标系，取g轴与h轴重合，逆时针旋转60°为h轴，图2(b)。设参考矢量为Vref(vα，vβ)，α-β坐标系到g-h坐标系变换公式为

(1)

由图2(b)可知，所有的电压矢量的坐标值均为整数，因此对于任意的空间参考矢量Vref(vrefg，vrefh)，计算得A扇区最近三矢量作用时间如表2示，表中T1、T2、T3与图2(b)所示的空间矢量相对应。

由表2可见，在60°坐标系下无需进行复杂的三角函数运算，仅含有简单的算术运算，极大地简化了SVPWM的运算，有利于在线实时控制。

表2 60°坐标系下A扇区中各个电压矢量占空比

3 传统三电平SVPWM空间矢量选择方案

按传统的SVPWM空间矢量选取方案[6]，即在最近三矢量调制下，遵循开关次数少、电压跳变小的原则，在图2(b)所示A3、A4小区中，选取的矢量作用序列分别为

A3：OON-PON-POO-PPO-PPO-POO-

PON-OON；

A4：ONN-OON-PON-POO-POO-PON-

OON-ONN。

同理，可知在对称的D扇区D3、D4(如图2(b)所示)的矢量序列为

D3：NNO-NOO-NOP-OOP-OOP-NOP-

NOO-NNO；

D4：NOO-NOP-OOP-OPP-OPP-OOP-

NOP-NOO。

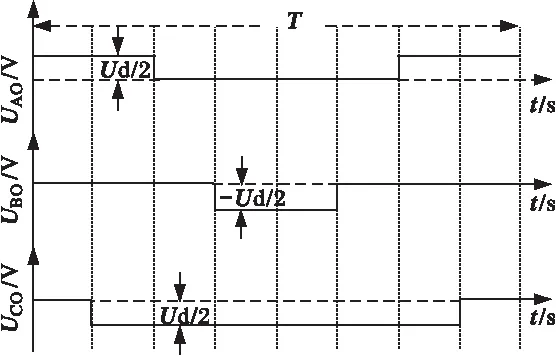
上述矢量序列在一个控制周期T内对应的逆变器输出电压如图3所示。

在上述矢量选取方案下，逆变器输出电压在空间180°的对称位置输出波形关于原点不对称(如图3中(a)与(c)、(b)与(d))，因此输出电压中含有偶次谐波。类似分析可知其他对称扇区中的波形也不满足奇对称。

图3 传统SVPWM算法的矢量序列波形

4 偶次谐波消去法的空间矢量选择方案

在采用脉宽调制技术时，逆变器输出相电压为一系列的周期性矩形波，且满足狄利克雷条件，因此，可以分解为傅里叶级数，即满足

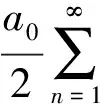
(2)

式中，ω为调制信号的角频率。

由式(2)知，欲消除偶次谐波，F(ωt)必须为半波对称的奇函数，即满足

F(ωt)=-F(ωt+π)=-F(-ωt)

(3)

此时有

(4)

由上一节分析知，传统SVPWM法控制时，逆变器输出电压波形不满足上述条件，其输出电压中含有偶次谐波。从图2(a)中可以发现，在选取电压矢量时有顺时针和逆时针的选取方法，且两种选取方法都不影响参考电压矢量的合成，也满足传统SVPWM空间矢量的选取原则，但控制性能不同。以A扇区A4小区为例，满足要求的矢量序列有：

(1)ONN-OON-PON-POO-POO-PON-OON-

ONN，即图3(b)所示；

(2)POO-PON-OON-ONN-ONN-OON-PON-

POO。

如果从空间位置上观察矢量序列(1)、(2)的首发三矢量，可知序列(1)矢量按顺时针方向合成参考矢量、序列(2)按逆时针合成参考矢量，定义顺时针合成为“+”，逆时针为“-”，如图4所示。而A4序列(2)恰好与图3(d)180°对称，如图5(a)所示。同理，由于三电平逆变器各扇区的对称性，修改其它区的矢量序列合成方向，可使逆变器输出电压波形半波奇对称，从而满足消除偶次谐波的要求。传统三电平SVPWM矢量合成序列和改进后的矢量序列对比如图6所示，阴影区域为需要修改序列合成方向的区域，并且显示的符号为已修改序列的合成方向；其他区域与传统矢量合成一致。

(a) 顺时针

(b) 逆时针

(a) A4序列

(b) D3序列

图6 偶次谐波消去法的空间矢量合成序列

5 仿真分析

为了验证本文提出的偶次谐波消去SVPWM算法，针对三相异步电机负载进行了仿真研究。所采用的电机参数为：PN=4 kW，Un=380 V，fN=50 Hz，ns=1 430 r/min，Rs=1.405 Ω，Rr=1.395 Ω，极对数pn=2，定、转子漏感分别为Lsl=Lrl=5.893 9 mH，互感Lm=0.172 2 H，其余采用默认值。取电网电压频率fs=50 Hz、载波频率fc=5 kHz、电机负载TL=10 N·m、直流母线电压Ud=500 V、调制系数k=0.76时，在传统的SVPWM空间矢量选取方案下，逆变器稳态运行时的线电压Uab谐波特性仿真波形如图7和图8所示，基波(50 Hz)有效值为382.3 V，总谐波畸变率(THD)为2.30%；在改进方案下相应的仿真波形如图9和图10所示，基波(50 Hz)有效值为382.9 V，总谐波畸变率(THD)为2.03%。

图7 传统矢量序列中性点悬浮时Uab频谱特性

图8 传统矢量序列中性点箝位于母线电压中点时Uab频谱特性

由上述仿真结果可以看出：采用传统矢量序列时，输出电压中含有偶次谐波，如图7和图8所示；而改进后的矢量序列能显著地消除偶次谐波，如图9和图10所示。但由于只是重新安排电压矢量的合成顺序，因此总的谐波含量几乎不变。在中点电位悬浮时，中点电位依然存在波动，因此线电压中仍存在较大的2、4次偶次谐波。但在母线电容中点箝位于母线电压中点时，在改进型矢量序列下能完全消除偶次谐波(见图10)，而传统矢量序列谐波特性并没有得到明显改善(见图8)。

图9 改进型矢量序列中性点悬浮时Uab频谱特性

另外，在仿真中还发现改进后的SVPWM开关频率也有少量的增加，这是因为改进后的矢量序列由图6中阴影区域切换到非阴影区域时会出现两相开关同时切换的现象而在传统选取方案中只有一相开关切换。

图10 改进型矢量序列中性点箝位于母线电压中点时Uab频谱特性

6 结语

本文在阐述NPC逆变器空间矢量模型和60°坐标系SVPWM算法的基础上，分析了传统SVPWM矢量选取方案产生偶次谐波的原因，继而深入探讨了消去偶次谐波的改进型空间矢量选择方案。仿真证实，该方案在满足传统NPC逆变器SVPWM法矢量选取原则的条件下，能有效地消除偶次谐波、抑制中点电位波动。但由于只是重新安排电压矢量的合成顺序，因此总的谐波含量几乎不变；同时，因中点电位存在波动，使得输出波形中仍含有2、4次谐波，如能将该方法与有效的中点电位抑制策略结合起来，达到完全消除偶次谐波的目的，将具有更大的实用价值。

[1] Pou J, Boroyevich D, Pindado R. Effects of imbalances and nonlinear loads on the voltage balance of a neutral-point-clamped inverter[J].IEEE Trans on Power Electronics, 2005, 20(1): 123-131.

[2] 费万民，张艳莉，阮新波，等(Fei Wanmin, Zhang Yanli, Ruan Xinbo,etal). 三电平逆变器SHEPWM非线性方程组的求解(Solutions to the SHEPWM non-linear equations for three-level voltage inverters)[J].中国电机工程学报(Proceedings of the CSEE)，2008, 28(6): 62-68.

[3] 胡存刚，王群京，夏秋实，等(Hu Cungang，Wang Qunjing，Xia Qiushi,etal). 三电平逆变器SHEPWM优化方法的研究(Optimization method for SHEPWM applied to Three-level inverter)[J].电力电子技术(Power Electronics), 2007,41(10): 90-92.

[4] Bendre Ashish, Krstic Slobodan, Vander Meer James,etal.Comparative evaluation of modulation algorithms for neutral-point-clamped converters[J].IEEE Trans on Industry Applications, 2005, 41(2): 634-643.

[5] 李国丽，夏秋实，胡存刚，等(Li Guoli, Xia Qiushi, Hu Cungang,etal).三电平NPC逆变器SVPWM方法研究(SVPWM algorithm for three-level NPC inverter)[J].电气传动(Electric Drive)，2007，37(12)：31-34.

[6] 宋文祥，陈国呈(Song Wenxiang, Chen Guocheng). 三电平中点箝位式逆变器SVPWM方法的研究(Study on SVPWM method for three-level neutral-point-clamped(NPC) inverter)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2004, 23(4): 30-33.

[7] 郑宗校，伦利(Zheng Zongxiao, Lun Li).多电平逆变器的简化SVPWM方法(Simpler method of SVPWM based on mutli-level inverter)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2008, 20(6): 124-128.

[8] 高红专，张志文，王磊，等(Gao Hongzhuan, Zhang Zhiwen, Wang Lei,etal). 基于DSP的三电平逆变器SVPWM算法的研究(Research on SVPWM algorithm for DSP based three-level inverter)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2006, 18(4): 62-66.

EvenOrderHarmonicEliminationMethodofThree-levelNeutralPointClampedInverter

LIU Bin， XUE Yu-qiang

(College of Electrical Engineering & Automation, Fuzhou University, Fuzhou 350108, China)

To overcome the drawback of the conventional space vector pulse with modulation(SVPWM)method applied to neutral point clamped(NPC)three-level inverter,which produces even order harmonics in the inverter output voltages,a new SVPWM shceme was proposed.The even order harmonics can be eliminate and the neutral voltage drift is suppressed by rearranging the vectors in the propsed method.Furthermore,the 60°coordinate frame is introduced to alleviate the computation cost.Simulation results results verify the validity of the scheme.

even order harmonic elimination； neutral point clamped(NPC) three-level inverter； vector selection； space vector pulse with modulation(SVPWM)； half wave odd symmetry

2010-08-05

2010-10-12

TM301.2

A

1003-8930(2011)01-0080-06

刘 斌(1985-)，男，硕士研究生，研究方向为电工理论新技术及应用。Email:liubin_0733@126.com 薛毓强(1962-)，男，硕士，副教授，硕士生导师，研究方向为电工理论新技术及应用。Email:yuqiang@fzu.edu.cn