开关型功率放大器缓冲电路的多目标优化设计①
2011-10-30孙晓明高孟平刘涤尘袁荣湘
孙晓明, 高孟平, 刘涤尘, 王 静, 向 农, 袁荣湘
(1.云南电网公司博士后科研工作站, 昆明 650217; 2.武汉大学电气工程学院, 武汉 430072; 3.云南电力调度中心, 昆明 650011 )
开关型功率放大器缓冲电路的多目标优化设计①
孙晓明1,2, 高孟平3, 刘涤尘2, 王 静2, 向 农2, 袁荣湘2
(1.云南电网公司博士后科研工作站, 昆明 650217; 2.武汉大学电气工程学院, 武汉 430072; 3.云南电力调度中心, 昆明 650011 )
对开关型功率放大器(SPA)缓冲电路的选型、原理和优化设计进行研究。依据原理分析,缓冲电路的设计任务被归结为求解一具有3个目标函数的多目标优化问题(MOP)。该文选择了目前解决MOP最有效的Ⅱ型非支配排序遗传算法(NSGA-Ⅱ)对以上MOP进行求解。为使求解过程更加高效,该文通过引入带前加速的拥挤距离分配(PACDA)、无重串的繁殖(RWD)、指针分组快速非支配排序(PGFNS)和带混沌因子的中间重组(CFBMR)4个策略对NSGA-Ⅱ进行了改进,提出了改进的NSGA-Ⅱ(MNSGA-Ⅱ)。仿真实验表明,MNSGA-Ⅱ较之NSGA-Ⅱ更加有效和快速;而试验证明,由MNSGA-Ⅱ寻找到的缓冲电路的最优参数使设计充分达到了预期的目标。
开关型功率放大器; 缓冲电路; 多目标优化问题; Ⅱ型非支配排序遗传算法; 优化设计
缓冲电路在大功率变流器中对降低开关损耗、延长器件使用寿命、提高整机效率和减小电磁干扰方面发挥着重要作用。文献[1,2]报道了以逆变器为代表的开关型功率放大器SPA(switching power amplifier)在继电保护测试装置PRTE(protective relay testing equipment)电力故障波形重现[3,4]功能中的成功应用,但所述电路仅为便于分析的拓扑,并非实际电路,因实际电路还需附加缓冲电路(或称吸收电路)等辅助电路。
根据不同的原理,缓冲电路可分为无源[5]和有源[6]缓冲电路、有损[7,8]和无损[5]缓冲电路、有能量再生能力[9,10]和无能量再生能力的缓冲电路开通、关断和开通/关断缓冲电路[9]。
文献[5]和文献[11,12]对DC-DC变换器的缓冲电路的原理和设计方法进行了研究,但其结果不能直接移植到SPA的缓冲电路,因两者的主电路不同。文献[6~10]所研究的缓冲电路主要用于大功率变流器,对效率的要求很高。然而,PRTE这类用量大、换代快的实验设备,并不要求很高的效率;相反,更重视便携性和高性价比。SPA是PRTE的核心,故要求其器件少、体积小、重量轻、成本低,显然对其缓冲电路也不例外;其中体积小意味着器件的安装密度大,要求缓冲电路能最大限度地抑制开关噪声,降低传导型或辐射型干扰对邻近部件的影响。因此,对SPA的缓冲电路,首要关注的是噪声抑制能力,其次是所用器件的数量、体积、重量和成本,而对功耗的要求则可适当放宽。可见,SPA缓冲电路的设计目标与文献[6~10]不同。
此外,文献[5~12](除文献[7])仅对其缓冲电路原理进行了研究,未对缓冲电路参数进行优选;尽管文献[7]对其缓冲电路的参数进行了多目标优化,但采用的模糊优化方法本质上是一种目标函数加权法OWM(objective weighting method)[13],OWM通过对各目标函数加权求和将多目标优化问题MOP(multiobjective optimization problem)转化为单目标优化问题求解,虽简便易行,但仅能得到1个非支配解,这在已知最优目标函数值而寻求一近似最优解时很快捷,因为可将所求得的唯一非支配解的目标函数值与已知最优目标函数值比较,确定该解的优良程度;然而在无法预知最优目标函数值时(缓冲电路的优化设计即如此),仅能保证OWM得到的那1个解为非支配解,却不能保证其为最优解,若盲目采用之,则可能导致决策结果事与愿违。其次,实际问题的各目标函数的量纲、数量级通常不一致,对其赋上无单位的权值就此一视同仁并求和,会使最终产生的那个单一的目标函数毫无物理意义,若数量级相差太大还可能使算法无法运行。最后还需指出,文献[7]通过引入器件的单位价格因子将缓冲电路的投资单独定为一优化目标,这虽直接反映了对性价比的期望,但各器件的单位价格因子受市场影响较大,在实用中难以准确把握;另外,文献[7]在其目标函数中用到了缓冲二极管的平均电流和缓冲电阻的平均功率,但未给出前者的具体计算公式,而后者的计算公式则引自文献[6],但文献[6]的公式含有较多经验成分,在理论上缺乏严谨的可溯源性。
鉴于上述,为提高性价比,首先对9种无源有损缓冲电路进行了对比,确定出最佳的结构类型;并将所选缓冲电路置于SPA中对其工作原理进行了详尽的分析和计算,推导了缓冲二极管平均电流和缓冲电阻平均功率的计算公式。基于分析、计算产生的公式,对缓冲电路的参数进行优选,优选由求解一具有3个目标函数的MOP实现。选用由非支配排序遗传算法[13]NSGA(nondominated sorting genetic algorithm)发展而来的NSGA-Ⅱ[14,15]方法来求解以上MOP。通过引入带前加速的拥挤距离分配PACDA(preaccelerating crowding distance assignment)、无重串繁殖RWD(reproduction without duplicates)、指针分组快速非支配排序PGFNS(pointers grouping fast nondominated sort)和带混沌因子的中间重组CFBMR(chaotic factor based middle recombination)4个策略对NSGA-Ⅱ进行改进,提出了改进的NSGA-Ⅱ(modified NSGA-Ⅱ,MNSGA-Ⅱ)。仿真结果表明MNSGA-Ⅱ较之NSGA-Ⅱ更加有效和快速。试验结果表明,由MNSGA-Ⅱ寻找到的优化参数使缓冲电路充分达到了预期的设计目标。
1 缓冲电路的选型
可选的无源有损缓冲电路按结构复杂程度由简至繁依次示于图1中。其中:R、C、D、L分别为缓冲电阻、电容、二极管和电感;T为所用器件总数。图1(i)最复杂、使用器件最多,图1(a)~(h)均可视为图1(i)经不同程度简化后的结果;然而,缓冲电路的性能需视具体情况依试验而定。
为选择最佳的缓冲电路类型,本文将各缓冲电路依次接入SPA进行试验。因试验波形数量繁多,不便罗列,故在此省略之,仅给出试验的结论:
(1)在抑制关断尖峰电压方面,(a)≤(b)≈(c)<(e)<(d)≈(f)<(g)≈(h)≈(i)。由(d)≈(f)和(g)≈(h)≈(i)可知,缓冲电感对性能的改善并不明显,且若缓冲电感过大还会带来较大的关断过渡电压,这是因为线路的杂散电感已足够大,故可省略缓冲电感。
(2)在保证开关波形上升/下降沿的陡峭程度方面,(i)<(f)<(h)<(c)≈(d)≈(e)≈(g)<(b)<(a)。可见较大的缓冲电感和缓冲电容均会降低开关波形上升/下降沿的陡峭程度,从而给输出的PWM脉冲带来误差;这再次表明缓冲电感应略去,且应限制缓冲电容的容量。
(3)在损耗或发热量方面,(g)<(h)≈(i)<(e)<(d)≈(f)≈(c)<(a)≈(b)。可见单缓冲电路(2个开关器件共用1个缓冲电路)的损耗比双缓冲电路(2个开关器件各用1个缓冲电路)大,这是因为采用单缓冲电路时2个开关器件中总有1个工作在接近于硬开关的状态。综观以上3组排序及各电路所用器件的数量,(g)和(h)成为首选;但因(h)为一开通/关断缓冲电路[6],而(g)为一关断缓冲电路,故(h)的损耗大于(g),所以(g)成为最佳选择。
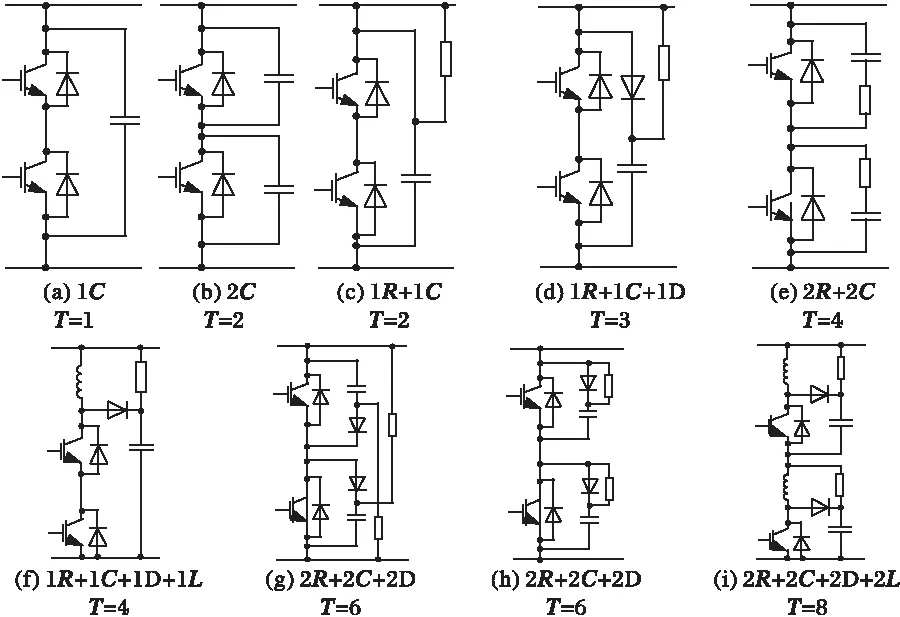
图1 缓冲电路的9种备选结构
2 所选缓冲电路的原理及其优化设计问题
2.1 配置方式及假设前提
缓冲电路的工作原理需与IGBT的开关过程联系起来研究。文献[11]采用线性函数对开关波形的上升/下降沿予以近似;而文献[10]和[10]则基于分段线性化的思想,用两段线性函数拼接来拟合开关波形的上升/下降沿;易推知,可用2次及更高次的函数对开关波形的上升/下降沿进行拟合。虽然后2种方法可使拟合结果更加贴近实际波形,但其却带来如下问题:分段线性化方法会造成拟合函数的定义在不同段上互不相同,这就使分析推导需按各段分别进行,十分复杂;而用2次及更高次的函数拟合会导致高阶非齐次微分方程,难以求得便于讨论的解析解。鉴于此两点,本文沿用文献[11]的方法以线性函数来拟合开关波形的上升/下降沿,即假设IGBT的开通上升电流iVon、关断下降电流iVoff分别为
iVon=IL0t/trt∈[0,tr]
iVoff=IL0(1-t/tf)t∈[0,tf]
(1)

图2 所选缓冲电路在SPA上的配置方式
2.2 关断缓冲过程分析
2.2.1 关断缓冲过程开始前瞬间(t=0-)
2.2.2 关断缓冲过程开始后至iV=0期间(t=0+~tf)

iL=iVoff+iCs=IL0(1-t/tf)+iCs
(2)
(3)
对式(3)两边求导后得微分方程
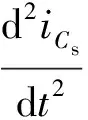
(4)
微分方程(4)的通解形式为
iCs=c1cos(ωst)+c2sin(ωst)
(5)
式中:c1、c2为待定常数;ωs=[2/(LstrCs)]1/2。由
(6)
可解得c1、c2,代入式(5)可得到最终的解为

(7)
当t=tf时,iV=iVoff=0,此时的uV=uCs称为关断过渡电压,记为UVT、UCsT,由式(3)和式(7)可求得
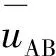
(8)
2.2.3iV=0至iCs=0期间(t=tf~ta)
在t>tf后V1、V4完全关断,iV=0,iCs(tf)=iL(tf)≠0;iCs虽将从iCs(tf)下降,但将继续对Cs充电,使uCs继续增加;到iCs=iL降为0时,uV=uCs达到最大值,称为关断尖峰电压,记为UVP、UCsP。此时有
(9)
对式(9)两边求导后得到一与式(4)相同的微分方程,故其通解形式相同,仅初始条件不同,为
(10)

iL=[IL0/(ωstf)]{sin(ωstf)cos(ωst)+
[1-cos(ωstf)]sin(ωst)}
(11)
设t=ta时iCs=iL减为0,令式(11)中的iL=0可解得
tan(ωsta)=-sin(ωstf)/[1-cos(ωstf)]
(12)
实践中有ωstf<<1<π/2,故sin(ωstf)>0;因此由式(12)可判断tan(ωsta)<0,即角ωsta处于直角坐标平面的第2或4象限。但因tf sin(ωsta)= (13) cos(ωsta)= (14) ta=π/ωs-(1/ωs)arctan{sin(ωstf)/[1- cos(ωstf)]} (15) 将式(11)、式(13)和式(14)代回式(9)可求得 (16) 2.2.4 关断过程中Ds的平均电流(t=0~ta) 上述表明,iDs=iCs在t=0~tf和t=tf~ta期间表达式分别为式(7)和式(11),将其代入 (17) 可求得iDs在t=0~ta期间的平均值。 2.2.5Rs在Cs放电过程中消耗的平均功率(t=ta~tb) (18) 对上式两边求导后得到微分方程为 (19) 此为二阶系统,其特征方程的根(系统的极点)为 (20) iCs=c1er1t+c2er2t (21) (22) 解出待定常数后,代入式(21)得到最终的解为 iCs=CsUCsP[er2(t-ta)- (23) 因|r2|>|r1|,除t=ta时iCs=0,t>ta后均有iCs<0,这说明iCs的实际方向与图2所示方向相反,与实际情况相符;此外,因er2(t-ta)比er1(t-ta)衰减快,iCs还将向负向增大,到达负向极大值iCsM后,随着Cs过剩储能的释放iCs又向正向减小,并最终衰减为0。令iCs的一阶导数为0,即可求得iCs=iCsM的时间t=tM为 tM=ln(r2/r1)/(r1-r2)+ta (24) 设计所关心的并不是tM,而是iCs从0向负向增加而后又向正向衰减至0所需的时间,即Cs整个放电过程所需的时间tb。理论上,iCs=0的解为t=ta或t=∞;然而t=ta是起始时刻,而t=∞毫无实用价值,因不知多大才算无穷大;故无法由iCs=0直接解出tb。为了解决该问题,本文定义tb为|iCs|由0增加至|iCsM|又由|iCsM|衰减至0.1|iCsM|的时间。但将0.1iCsM代入式(23)时会导致一超越方程er2(t-ta)-er1(t-ta)= 0.1[er2(tM-ta)-er1(tM-ta)],无法求得解析解,故本文采用一近似解法:因er2(t-ta)比er1(t-ta)衰减快,可预计当er1(t-ta)衰减至0.1er1(tM-ta)时,er2(t-ta)早已衰减至并小于0.1er2(tM-ta),故可将方程er1(t-ta)=0.1er1(tM-ta)的解近似作为tb,即 tb≈ln(0.1)/r1+tM (25) (26) 2.3 开通过程简述 2.4 优化设计问题的提出 (1)关断尖峰电压最小,即 (27) 此为设计的首要目标,因为UVP、UCsP越小,开关噪声及其干扰越小。其次,若UVP小,就可选用C-E极耐压VCES低的IGBT(在其余参数相同时,VCES低的IGBT价格较低);同样若UCsP小,就可选用耐压低的缓冲电容(在电容量相同时,耐压低的电容价格较低、体积较小),且无需通过串联来提高耐压。 (2)流过缓冲二极管的平均电流最小,即 minIDs(AV)= (28) 若IDs(AV)小,就可选用平均正向电流IF(AV)小的快恢复二极管(在其余参数相同时,IF(AV)小的快恢复二极管价格较低、体积较小、货源较充足)。 (3)缓冲电阻的平均功率最小,即 (29) PRs间接反映了开关损耗。若PRs小,则不仅开关损耗小,还可选用标称功率小的缓冲电阻(在阻值相同时,标称功率小的电阻价格较低、体积较小、发热量较小、货源较充足,自行制作也较方便)。 式(27)~式(29)构成一具有3个目标函数的MOP。不同于文献[7],本文将器件价格隐含地融入到3个目标函数中,仅考虑相对价格而不考虑绝对价格,避免了市场价格波动对优化设计的影响。 3.1 多目标优化问题的基本理论及NSGA-Ⅱ 前已提及,NSGA-Ⅱ的优势在于能同时保证非支配前沿的完备性和多样性:既能保证非支配前沿包含所有可能的非支配解,又能保证这些非支配解不集中于非支配前沿的某个局部,而是均匀地散布在整个非支配前沿上。在NSGA-Ⅱ搜索到的非支配前沿上进行二次择优,可获得全面、客观的决策结果。而对于不能同时保证非支配前沿完备性和多样性的方法[14](如OWM),在其搜索到的非支配前沿上所做出的二次择优势必带有局限性。此即本文选择NSGA-Ⅱ作为求解工具的原因。尽管NSGA-Ⅱ已十分有效,但笔者在实践中发现,其在拥挤距离分配(CDA)和新种群繁殖方面存在缺陷,若予以完善,不仅可消除程序可能出现的异常,还能提高算法的效率;而其在快速非支配排序(FNS)和重组方面存在性能提升的潜力,若引入适当的策略,可较大地提升算法的速度。 3.2 改进策略 3.2.1 带前加速的拥挤距离分配——PACDA NSGA-Ⅱ的CDA仅考虑了某非支配前沿上的解多于2个且各解不相等的情况,但①某非支配前沿仅有1或2个解、②某非支配前沿上的解均相等这2种特殊情况在种群进化前期发生率很高,若不进行适当处理,常会影响程序运行。以下分别讨论之。 (fi,max-fi,min) (30) 情况1式(30)表明,在已知序号为tk+1、tk和tk-1的3个非支配解时,才能计算序号为tk的解的拥挤距离;换言之,必须存在3个以上解时,讨论某个解与其周围解的临近/拥挤程度才有意义。当某非支配前沿仅有1或2个解时,均无拥挤程度可言,若仍按式(30)计算无意义的拥挤距离,则很可能导致异常。改进策略是取消拥挤距离的计算,直接赋以这1或2个解最大的拥挤距离,因其未被任何解包围。NSGA-Ⅱ定义最大拥挤距离为∞,其实因式(30)的求和项是小于等于1的非负数,故对∀tk,0≤dcrowd≤M。据此,可将∞设定为M,这样做既方便又可靠。 情况2当某非支配前沿上的解均相等时,意味着将出现fi,min=fi,max,这将使式(30)的分母为0,导致程序出错。此时的改进策略同样是取消拥挤距离的计算,而直接赋以各解最小拥挤距离0,因其紧密相连。 以上策略不仅使程序运行变得可靠,且在种群进化前期节省了很多无谓的运算,起到了加速的作用,故称为PACDA。 3.2.2 无重串繁殖——RWD NSGA-Ⅱ在产生新种群前,先将当前种群与经重组和变异后包含子个体的种群合并,对合并后的种群再次进行FNS和CDA,以实现父代与子代总体上的优选,由优选出的精英组成新一代种群。所谓精英,就锦标赛选择法而言,是指2个解中处于低编号非支配前沿的解或2个处于同一非支配前沿的解中拥挤距离大的解。因父代和子代具有较大的相似性,对合并后的种群进行FNS后,在所产生的非支配前沿上很可能出现多个相同非支配解堆积的现象,这就造成某些非支配解,从其所处的非支配前沿来看,编号很低,是较优良的精英,但却因其克隆体的产生,使其拥挤距离为0,导致其被选中并繁殖的机会大大降低,结果是这些较优良的精英反而被淘汰。 改进的策略是将NSGA-Ⅱ的有重串繁殖代之以RWD:在对1个非支配前沿进行CDA前,先将它与其自身进行求并集运算,使多个克隆体仅保留1个。这就保证了较优良的精英在CDA时能被公平对待,在优选时不致被轻易淘汰,也使后续的优选能更多地选到精英中的精英,从而间接地提高了算法的效率。 3.2.3 指针分组快速非支配排序——PGFNS NSGA-Ⅱ的FNS由比较和归并2个操作组成:比较指进行支配比较,以确定解p的支配数np(支配p的解的数目)和被支配解集Sp(被p支配的解的集合);归并指将具有相同np的解归类合并至同1个非支配前沿,从而形成若干非支配前沿,并按np由小到大进行编号,编号越小的非支配前沿的解越优良。在这2个操作中,为记录中间结果,FNS分配了L(L为种群规模)个Sp数组、有可能多至L个的非支配解集F1,F2,…及中介集合Q。可见,若按FNS实现,程序需开辟诸多浮点型存储空间,且不断地对浮点数进行操作和移动。然而,无论对于何种软件,操作或移动1个浮点数均比操作或移动1个整数所需的计算量、存储空间及对存储空间的访问次数要多得多。虑及FNS的运算量较大,且1次进化过程包含2次FNS,极大地制约着算法整体效率和运行速度。其改进策略如下。 策略1在经支配比较确定np后,将种群个体的指针与其np一起按由小到大的顺序排序,排序后种群个体的指针也按排序序号依次排列起来,与相同np对应的指针即被隐含地归并(分)为1组。这比FNS经支配比较后,还要将各解再由F1,F2,…及Sp中取出才能按np对号入座快捷得多。 策略2将支配比较换之以非支配比较,并经非支配比较确定出np=0的解p(包含若干个解),将其指针归并(分组)到非支配解集G0;将p的指针从当前种群的指针集合中去掉,使p不再参与确定后续非支配解集所需进行的非支配比较;经新1轮非支配比较,确定出np=1的解p(亦包含若干个解),将其指针归并到G1;以此类推,确定出所有可能的非支配解集。显然,随着G0,G1,…的依次确定,参与非支配比较的个体数将逐渐减少。虑及1次非支配/支配比较包含着若干次浮点数比较(关系运算),该策略较之策略1进一步减少了运算量,提高了效率。 应指出,1个解不受其自身支配,故在进行非支配/支配比较时,应避免这个解与其自身比较。 总之,以上2个改进策略均省去了FNS所需的各种数组,排序和归并操作均借助种群个体的指针间接完成,不移动个体本身,故种群的存储空间不发生任何变动,从而无需再为算法开辟大量额外的存储空间;除最底层的目标函数值比较外,其余运算基本上都为指针的加减运算,故算法的运行速度大大提升。因改进策略的核心是以指针的分组代替个体的分组,故将其命名为PGFNS。 3.2.4 带混沌因子的中间重组——CFBMR 本文拟求解的MOP是实际工程问题,希望在求解时能保持种群个体和目标函数的物理意义,以便于理解;而且,也希望求解结果有足够高的计算精度。故应首选无需解码操作且至少为32位精度的浮点数编码方式。在浮点种群的重组方法中,中间重组(MR)最简便,计算式为 oi=p1+α(p2-p1)=(1-α)p1+αp2 i=1,2,…,L (31) 式中:oi为父个体重组产生的第i个子个体;p1、p2为由锦标赛选择法挑选出的2个父个体,p1≠p2;比例因子α为在区间[0,1]上按均匀分布产生的随机数。均匀分布意味着等概率,故可预计oi与p1间出现较大差异(α接近于1)和差异不大(α接近于0)的概率各占50%。对于NSGA-Ⅱ,在种群进化中后期,种群已非常接近所求非支配前沿,有血缘关系的个体会以小群体的形式聚集在当前非支配前沿上,将非支配前沿分成若干不连续的段。为使这些小群体解除封闭,尽快均匀地散布到整个非支配前沿,以保持解的多样性,就希望新的解发生较大变化从而跳出局部解空间的概率稍大一些。 改进策略用混沌因子来代替α参与MR,借助于混沌因子极强的局部活动性[18~20]来加速种群向理想的非支配前沿,即解均匀等间隔分布的非支配前沿进化。通常由Logistic方程来产生混沌因子 βi+1=μβi(1-βi) i=1,2,… (32) 式中:∀βi∈[0,1];系数μ=4。此时式(32)描述的动力学系统处于完全混沌状态。将βi+1带入式(31)取代α,即得到CFBMR的公式为 oi=p1+βi+1(p2-p1)=(1-βi+1)p1+βi+1p2 (33) 3.3 算法流程 MNSGA-Ⅱ算法的N-S流程如图3所示。 图3 MNSGA-Ⅱ算法的N-S流程 4.1 基于测试函数的仿真验证 用优化结果已知的测试函数对MNSGA-Ⅱ的有效性进行仿真验证。因第3.2.1~3.2.3节的改进是围绕提高算法可靠性、降低运算量进行的,对算法性能的改善及速度的提升很直观,故不再刻意地对其进行验证;而第3.2.4节的CFBMR对算法性能的改善则不直观,故本节着重验证CFBMR对算法性能的改善。其次,限于篇幅本文无法给出多个测试函数的仿真结果,故仅选用了最经典的双二次函数问题对MNSGA-Ⅱ进行仿真测试。 双二次函数问题[13,14]的计算式为 minf1(x)=x2,f2(x)=(x-2)2 (34) 式中x的取值范围为整个实数域,其精确的非支配前沿为x∈[0,2],对应于f1(x)、f2(x)∈[0,4]。应指出,若采用OWM,并取f1(x)、f2(x)的权重系数同为0.5,则仅能求得x=1这个非支配解;显然,OWM毫无完备性和多样性可言。 现用MNSGA-Ⅱ求解双二次函数问题。仿真实验参数为M=2,L=100,浮点数编码,最大进化代数250,重组率0.8,育种机变异方法,变异率0.05。图5和图6分别示出了采用MR时和采用CFBMR时MNSGA-Ⅱ的进化过程,为公平起见,2个图均从图4所示的初始种群开始进化。 图4 图5和图6共同的初始种群 图5 采用MR时MNSGA-Ⅱ的进化过程 下面分析仿真结果。在前30代和50代(进化中前期),图6的种群比图5的种群进化快很多。到100代(进化中期),图5的种群还处于小群体状态,图6的种群已突破小群体局限开始均匀散布。分别对比150代、200代和250代(进化中后期),可见图6的种群在100代时已基本达到稳定,实践中继续进化到150代即可保证解的可靠性,并终止程序运行;而图5的种群则要进化到150代才基本达到稳定,故至少要进化到200代才能保证解的质量。由此可见,对于同一个初始种群,CFBMR使MNSGA-Ⅱ减少了近50代的运算量,这是相当可观的。另外,图5和图6均表明,在种群趋于或达到稳定后(150代 ~250代)继续对其进行操作,并不会打乱其稳定状态;相反,随着进化的继续,有更多异于当前解的解(拥挤距离更大的解)被找到,而使解的散布更加均匀。将MNSGA-Ⅱ进化至250代的结果(图5(f)或图6(f))与文献[14]的相同结果比较,会发现本文解的散布比NSGA-Ⅱ更均匀。以上分析和对比充分说明了MNSGA-Ⅱ十分快速、稳定和行之有效。 图6 采用CFBMR时MNSGA-Ⅱ的进化过程 4.2 缓冲电路参数的优化设计 本节将MNSGA-Ⅱ用于求解第2.4节的MOP,该MOP含有3个目标函数,比式(34)多1个;而且缓冲电路中需要且能够调整的参数为Cs和Rs,应将它们合并为2维解向量[Cs,Rs],这又比式(34)解的维数多了1维。然而这2点不同给4.1节的程序带来的改动是很少的,故本文不再赘述。此时除M=3和最大进化代数变为150(第4.1节已指出采用CFBMR时进化至150代就够了)外,算法的其余参数同第4.1节。此外还需补充若干电路参数:Ud=67 V[1,2],Lstr=63 nH,IL0=10 A[1,2],tf=0.6 μs。需说明的是,Lstr是用走线和过孔的寄生电感公式[21,22]按其在PCB上的尺寸计算得出的;本文采用PM30CSJ060型IPM构成图2的SPA主电路,tf由其技术资料查得。 图7 采用CFBMR的MNSGA-Ⅱ对缓冲电路参数的优化 图7示出了初始种群及进化至150代时的种群。图7(b)显示,150代时种群已较规则地收敛至1个三维的非支配前沿;虚线圈部分可视为最优解区域,缓冲电路的优化参数可依设计者的经验和倾向从该区域中选择。作为二次择优的示例,表1列出了最优解区域中的6组非支配解及其目标函数值。本文选用了表中的第4组参数,其UVP、UCsP最低,IDs(AV)最小,PRs略大。根据这组参数,可选择电容量为0.33 μF,耐压高于100 V的电容作为缓冲电容,且为保证良好的温度稳定性,最好采用CBB或CB电容;可选择电阻值为24 Ω,标称功率为3 W的金属膜电阻作为缓冲电阻;可选择IF(AV)大于2 A的快恢复二极管作为缓冲二极管,比如HFA04TB60,其IF(AV)=4 A,可留有近2 A裕度。 表1 6组非支配解及其目标函数值 4.3 缓冲电路优化参数的试验结果 本节将上节优选的缓冲电路参数及相应器件用于图2的SPA进行试验。图8分别示出了未使用缓冲电路时和使用参数经过优化的缓冲电路时SPA的开关波形。需说明,缓冲电路参数选取不当或所选参数非最优参数时的开关波形与未加缓冲电路时的开关波形比较类似,仅关断尖峰电压的幅值或开关脉冲上升沿的陡峭程度有所不同,故本文未再给出相应的开关波形。还需指出,图8所示为IGBT C-E极间的电压波形(因该波形便于用示波器直接观测),若将该波形上下颠倒一下,可大致得到IGBT的电流波形;其次,因IGBT正处于高速工作状态,PWM脉冲的宽窄迅速变化,图中所示波形实际上是多个宽窄不同的PWM脉冲相互叠加的综合效果。图8表明,带优选参数的缓冲电路不仅使关断尖峰电压基本上削减到了最小,且同时保证了开关脉冲上升沿的陡峭,其上升沿与未加缓冲电路时的上升沿基本一致(若参数选取不当,则上升沿可能向右倾斜)。图8(a)中还示出了UVT、UCsT、UVP、UCsP的定义及其与Ud的关系。 图8 2种情况下SPA开关波形的对比 应指出,通过测取Rs两端的平均电压(采用万用表的直流档)可估算出PRs≈2.26 W,这与计算值2.43 W(表1)是比较接近的(第2.1节已指出,本文的理论推导带有一定的保守性),故这从定量的角度验证了本文理论推导及优化算法的正确性。因IDs(AV)不易直接测量(若串接电流表测量,很可能会改变回路的等效杂散电感),故本文未能给出其实际测量值。 本文对SPA的缓冲电路进行了详细研究。研究包括电路选型、原理分析和优化设计3部分。基于对所选缓冲电路的原理分析,优化设计任务被归结为求解一具有3个目标函数的MOP。为求解该MOP,本文提出了基于PACDA、 RWD、PGFNS和CFBMR 4个策略的MNSGA-Ⅱ,测试函数的仿真实验验证了MNSGA-Ⅱ的稳定性、快速性和精确性。此后本文将MNSGA-Ⅱ用于求解缓冲电路参数的MOP,并将优选的参数用于实际电路,试验结果表明,优选的参数使缓冲电路充分达到了预期的设计要求。最后要指出的是,本文所提出的4个改进策略除简便易行外,还具有通用性,可为同类方法所借鉴;其次,本文对SPA缓冲电路的分析及优化设计方法同样可为大功率变流器的缓冲电路所借鉴,只需将优化目标做适当调整,即可得到相应的优化设计结果。 [1] 孙晓明,刘涤尘,黄涌,等(Sun Xiaoming,Liu Dichen,Huang Yong,etal).一种基于电源周期平均模型的单相PWM逆变器准PID控制器(A quasi-PID controller of single-phase PWM inverter based on source period averaging model)[J].中国电机工程学报(Proceedings of the CSEE),2006,26(24):50-54. [2] Sun X M,Long H L,Liu D C,etal.Adaptive control of protective-relay-testing inverter[C]∥IEEE 6th International Power Electronics and Motion Control Conference,Wuhan,China:2009. [3] 孙晓明,杜新伟,刘涤尘,等(Sun Xiaoming,Du Xinwei,Liu Dichen,etal).基于数字闭环修正技术的故障重现放大装置(The obstacle recurrence and amplification device based on digital closed-loop modification technology)[J].电力系统自动化(Automation of Electric Power Systems),2004,28(4):49-53. [4] Sun X M,Liu D C,Long H L,etal.The design of an electrical fault-waveform regenerator[C]∥International Conference on Electrical Machines and Systems, Wuhan,China:2008. [5] 杜忠,陈治明,严百平(Du Zhong,Chen Zhiming,Yan Baiping).一种基于BOOST变换器的无源无损吸收方法(A passive lossless snubbers method based on BOOST converter)[J].电工技术学报(Transactions of China Electrotechnical Society),2003,18(4):35-40. [6] Chokhawala R S,Sobhani S.Switching voltage transient protection schemes for high-current IGBT modules[J].IEEE Trans on Industry Applications,1997,33(6):1601-1610. [7] 唐欣,罗安,李刚(Tang Xin,Luo An,Li Gang).大功率绝缘栅双极晶体管模块缓冲电路的多目标优化设计(Multi-objective optimal design of Snubber circuits for high power IGBT modules)[J].中国电机工程学报(Proceedings of the CSEE),2004,24(11):144-147. [8] 曹解围,毛承雄,陆继明,等(Cao Jiewei,Mao Chengxiong,Lu Jiming,etal).配电系统电力电子变压器的IGBT缓冲电路设计(Design of IGBT snubbers for electronic power transformer in distribution system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(6):71-74. [9] He Xiangning,Deng Yan,Williams B W,etal.A simple energy recovery circuit for high-power inverters with complete turn-on and turn-off snubbers[J].IEEE Trans on Industrial Electronics,2004,51(1):81-88. [10]Swanepoel P H,van Wyk J D.Analysis and optimization of regenerative linear snubbers applied to switches with voltage and current tails[J].IEEE Trans on Power Electronics,1994,9(4):433-442. [11]陈坚.电力电子学-电力电子变换和控制技术[M].2版.北京:高等教育出版社,2004. [12]林渭勋.现代电力电子电路[M].杭州:浙江大学出版社,2002. [13]Srinivas N,Deb K.Multiobjective optimization using nondominated sorting in genetic algorithms[J].Journal of Evolutionary Computation,1995,2(3):221-248. [14]Deb K,Pratap A,Agarwal S,etal.A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J].IEEE Trans on Evolutionary Computation,2002,6(2):182-197. [15]苏慧玲,王淳,秦茹静,等(Su Huiling,Wang Chun,Qin Rujing,etal).基于GA改进算法的多目标机组优化检修计划(Multi-objective optimization of unit mainte nance scheduling based on improved GA)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2008,20(6):27-30. [16]夏德铃.自动控制理论[M].北京:机械工业出版社,2000. [17]王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002. [18]许传敏,杨洪耕(Xu Chuanmin,Yang Honggeng).电压波动估计的混沌简化粒子群算法(Chaotic simple particle swarm optimization algorithm for voltage fluctuation measurement)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(3):18-22. [19]蒙文川,邱家驹(Meng Wenchuan,Qiu Jiaju).电力系统经济负荷分配的混沌粒子群优化算法(Chaotic particle swarm optimization algorithm for economic load dispatch of power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(2):114-119. [20]刘宝英,杨仁刚,李慧,等(Liu Baoying,Yang Rengang,Li Hui,etal).基于混沌遗传算法的电力系统无功优化(Reactive power optimization based on chaos genetic algorithm in electric power systems)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2006,18(5):49-52. [21]Douglas B.Signal Integrity Issues and Printed Circuit Board Design[M].北京:机械工业出版社,2005. [22]江思敏.PCB和电磁兼容设计[M].北京:机械工业出版社,2006. MultiobjectiveOptimizationDesignofSnubbersforSwitchingPowerAmplifier SUN Xiao-ming1,2, GAO Meng-ping3, LIU Di-chen2, WANG Jing2, XIANG Nong2, YUAN Rong-xiang2 (1.Postdoctoral Scientific Research Institution of Yunnan Power Grid Corporation, Kunming 650217, China; 2.School of Electrical Engineering,Wuhan University,Wuhan 430072, China; 3.Yunnan Electric Dispatch Center, Kunming 650011, China) The type selection,principle and optimization design of snubber circuit for switching power amplifier(SPA)were studied in the paper.Based on the principle analysis,the task of snubber circuit design was summarized as solving a multi-objective optimization problem(MOP)with 3 objective functions.Non-dominated sorting genetic algorithm-Ⅱ(NSGA-Ⅱ),known as the most effective mthod for solving the MOPs at present,was chosen to solve above MOP.In order to make the solving procedure more efficient,4 schemes,i.e. the pre-accelerating crowding distance assignment(PACDA),the reproduction without duplicates(RWD),the pointers grouping fast non-dominated sort(PGFNS)and the chaotic factor based middle recombination(CFBMR),were introduced to modify the NSGA-Ⅱ and the modified NSGA-Ⅱ(MNS GA-Ⅱ)was proposed.Simulation shows that MNSGA-Ⅱ is more effective and speedier than NSGA-Ⅱ;and experiment demonstrates that with the optimal parameters sought out by MNSGA-Ⅱ,the snubber circuit will achieve desired goals. switching power amplifier; snubber circuit; multi-objective optimization problem; non-dominated sorting genetic algorithm-Ⅱ; optimization design 2009-12-04 2010-04-06 国家自然科学基金资助项目(50677046) TM464 A 1003-8930(2011)01-0006-11 孙晓明(1980-),男,博士,IEEE Member,中国电机工程学会会员,博士后研究人员,研究方向为电力电子、继电保护测试技术、嵌入式系统和现代信号处理。Email:xmsun.whu@163.com 高孟平(1966-),男,教授级高级工程师,云南电力调度中心主任,博士生导师,研究方向为电力调度运行管理。Email:gmp@vip.sina.com 刘涤尘(1953-),男,博士,教授,博士生导师,IEEE Member,中国电机工程学会常务理事,主要从事电力系统自动监控、电力系统稳定与控制、电力电子及灵活交流输电系统等方面的研究。Email:dchliu@whu.edu.cn 王 静(1977-),女,博士,讲师,研究方向为电力电子和电力通信。Email:jwang@whu.edu.cn 向 农(1963-),女,博士,副教授,研究方向为电力自动监控。Email:nxiang@whu.edu.cn 袁荣湘(1965-),男,博士,教授,博士生导师,研究方向为电力系统继电保护、电力系统稳定。Email:rxyuan@whu.edu.cn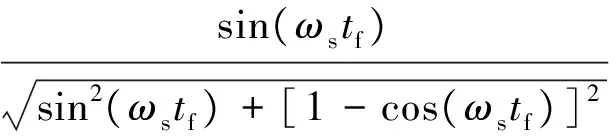


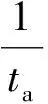


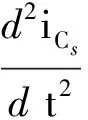







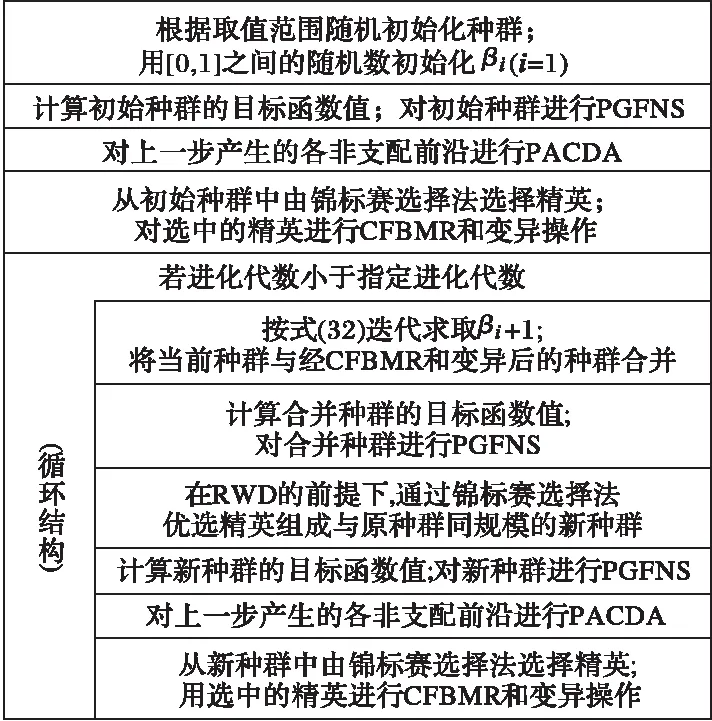
3 改进的NSGA-Ⅱ——MNSGA-Ⅱ


4 仿真验证及缓冲电路参数的优化设计






5 结语
