引入赫希曼指数的电力系统谐波分析①

苏广宁， 严 正， 杜 浩

(上海交通大学电气工程系电力传输与功率变换控制教育部重点实验室， 上海 200240)

引入赫希曼指数的电力系统谐波分析①

苏广宁， 严 正， 杜 浩

(上海交通大学电气工程系电力传输与功率变换控制教育部重点实验室， 上海 200240)

快速傅里叶变换是进行电网谐波分析的最主要方法，但是由于实际应用中只能截取有限长序列分析，从而必然产生误差。为了提高谐波分析的精度，该文提出了引入垄断经验学中的赫希曼指数(HHI)，来衡量频谱的集中程度，从而得到参与傅里叶变换的最佳序列长度。其中，采用Good-Thomas算法对任意长度序列进行快速准确地基本快速傅里叶变换计算，数据源为80点/周波现场实测Comtrade数据。通过仿真证实，其效果非常显著。并用Qt跨平台语言，实现了基于上述算法的电力系统谐波分析软件。

谐波； 快速傅里叶变换； 赫希曼指数； 序列长度

近年来，随着科学技术的快速发展，电力系统中出现了大量非线性元件，如输电系统中的换流设备等，而负荷中的非线性元件更是数不胜数，如电弧炉、电气化铁路、变频设备、电焊机等等。这些非线性元件产生的谐波注入到电网中会对电力系统造成很多不利的影响，威胁到电力设备的安全经济运行。对电网中的谐波进行准确的监测，是进行谐波治理的基础，其意义非常重大。进行谐波分析的最常用方法是快速傅里叶变换FFT(fast Fourier transform)。

在应用FFT的过程中，很多工作者认为，参与傅里叶变换的序列越长，得到的结果越准确。本文将证明这是一种误区，并提出了一种借用垄断经济学中的赫芬达尔-赫希曼指数HHI(Herfindahl-

Hirschman index)，简称赫希曼指数，来改进谐波分析精度的算法。最后，编写了基于跨平台语言Qt的电力系统谐波分析软件。

1 关于Fourier变换长度选择的误区

很多技术人员都存在这样一种共识，在进行傅里叶变换的时候，如果采样信号已经确定，那么每次参与变换的序列越长，即N越大，则得到的频谱愈接近于理论值。应该说，在N可以取得非常大的时候，这种说法是正确的，因为此时非整数周期的截断效应已经可以忽略。但实际情况并非如此，可以截取的N总是很有限的，它是否取得越大越好呢?下面做出分析。

设离散信号x(n)中含有L种谐波分量为

(1)

考虑到系统中间谐波的存在，ωi不一定为基波ω0的整数倍。用离散傅里叶变换DFT(discrete Fourier transform)的定义将其展开

k=0，1，…，N-1

(2)

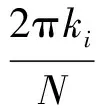
经过较复杂的推导，得只含三角函数的式子为

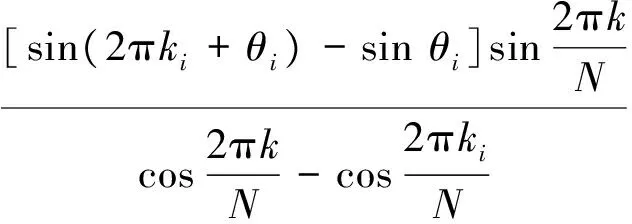
(3)

由式(3)对ki进行如下讨论。

(1)当所有的ki都能取到整数时，根据三角函数的周期性，由(3)看出，除了当k=ki时X(k)≠0，其他的X(k)均为0。

(2)ki不能都取到整数时，会发生频谱泄漏。

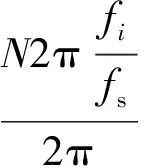
(4)

式中：fs为采样频率；fi为i次谐波频率。

若系统中只含有整数次谐波，即i只取整数，则只要使截断后的序列长度为原始信号中基波周期(最大周期)的整数倍，就可以得到准确频谱。在实际电力系统中，无论按标准取80点/周或是256点/周，只要截取长度为整周期数，就可以使ki为整数。

但事实上，系统中由于间谐波的存在以及频率的波动，使得无论N取多少，ki都不可能总为整数，进行频谱分析时存在频谱泄漏是不可避免的。应该尽量使ki接近整数，由式(4)知，这可以通过调整N实现。

由式(3)可以看出，频谱泄漏的多少与N的关系并不明确，为此，通常认为序列越长，谐波分析越准确的结论是否正确。下面通过一个实验来推翻这种论断，同时实验的过程本身就是一种提高傅里叶分析精度的算法。

2 计及HHI的电力系统谐波分析

首先，要确定一个衡量频谱泄漏多少的指标。在数字信号处理的相关文献中，尚未看到这种定义。据了解，在宏观经济学中，有若干用于衡量市场集中度(market concentration rate)的指标，如：行业集中率、赫尔芬达尔-赫希曼指数、洛仑兹曲线、基尼系数、逆指数和熵指数等。其中赫希曼指数(HHI)既反映了行业的集中度，又体现了该行业中企业的规模分布。它同时具有数学上绝对法和相对法的优点，从而成为了较理想的市场集中度计量指标，经常运用在反垄断经济分析之中。[2]它的计算公式为

(5)

式中：Si是第i个企业所占市场份额；n是这个行业中企业总数。

下面就用赫希曼指数来作为衡量频谱集中程度的指标，参与傅里叶变换的序列长度N在一个区间内连续取不同的值，观察HHI(n)的大小变化，并取HHI(n)最大时的序列长度N，作为最终参与FFT的序列长度。

这里，输入信号的幅度-频率分布采用高斯函数形式为

φ(f)=ae-(f-b)2/c2

(6)

其中a、b与c为实数常数，且a>0。采用该函数是因为c2=2的高斯函数是傅里叶变换的特征函数。这就意味着高斯函数的傅里叶变换不仅仅是另一个高斯函数，而且是进行傅里叶变换的函数的标量倍。这就使很容易估计出变换后频谱的形状，从而直观地判断频谱泄漏的大小。具体实验如下。

幅度-频率分布函数指数部分除以20，是为了让不同频率谐波的幅值相差不要超过一个数量级，否则在输出的高斯分布图上就无法清楚地看到两边的分量。采样间隔取0.008 123 s，这样避免被整除，使结果更具说服力，另外它小于0.01 s，即fs>100 Hz，满足采样定理，避免产生频谱混叠。实验结果如下。

输入信号的理论频谱如图1所示。

图1 原始输入信号的高斯分布频谱

取参与傅里叶变换的点数N在1 000～2 000点之间变化。由图2所示，在N取1 231点时，HHI最大。用1 231点参与傅里叶变换的频谱分布图如图3，可以看到，它同样是很好的高斯分布，分析精度很高。而当取最大点数2 000点参与傅里叶变换时，频谱分布如图4所示，它已经远远偏离高斯分布，分析的精度很差。

图2 HHI随输入序列长度变化曲线

从图2还可以看到，参与傅里叶变换的点数从1 000变到2 000的过程中，HHI在1 231点取得最大值，而且整个趋势是随着参与傅里叶变换的点数的增多而递减的，这与通常人们认为的参与傅里叶变换的点数越多越好的常识是相悖的。

在实际的电力系统当中，由于频率的波动以及间谐波的存在，当截取有限长序列进行分析时，必然会产生截断效应，引起泄露。上述算例是在一个输入波形的谐波次数为随机数的情况下完成的，很有代表性地验证了，存在这样一个最优序列长度，可以使HHI最大，即泄露最小。正如1中所分析的，此时的N，根据式(4)，可以使ki最接近整数。

图3 按HHI最大的1 231点计算出的频谱

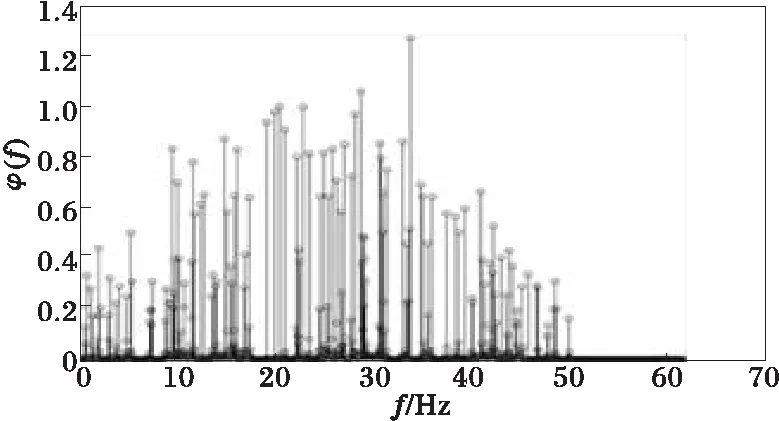
图4 按点数最多的2 000点计算出的频谱

3 基于Qt语言的谐波分析软件实现

考虑上述算法，笔者编写了基于Qt语言的电力系统谐波分析软件。Qt是Linux下的强大编程工具，它的最大优点是可以实现跨平台编译。目前变电站监控系统普遍采用Windows系统，但是出于对电力系统安全的考虑，已经逐步开始将Linux和Solaris系统引入到电力系统当中。因此，基于Qt语言编写的谐波分析软件，可以更好的适应未来电力系统的发展。

数据源采用80点/周的现场实测Comtrade数据。软件中实现了上述算法，即可自动选择最优序列长度进行计算，提高了离线谐波分析的精度。

为了可以快速准确地进行任意长度序列的FFT，采用了以Winograd小NDFT算法为基础的Good-Thomas算法做基本运算[3，4]。这种算法将长度为N=N1×N2的一维DFT转换成尺寸为N1×N2的二维DFT，然后以行-列方式沿每一维采用最有效的算法计算这个二维的DFT。它的运算效率比分裂基FFT更高，当然编程也更复杂。

图5 基于Qt语言的电力系统谐波分析软件

4 结语

本文是在笔者编写基于现场实测80点/周Comtrade文件数据的谐波分析软件过程中，遇到的实际问题而写的。文中提出了一种引入垄断经济学中的赫希曼指数作为衡量频谱泄漏指标的算法，由仿真结果可以看出，该方法对提高谐波分析的精度有很大的帮助。最后实现了基于跨平台编译语言

Qt和该算法的谐波分析软件。其中为了可以快速对任意长度序列进行FFT计算，采用了Good-Thomas算法。

[1] 周厚奎，张昱，金心宇(Zhou Houkui, Zhang Yu, Jin Xinyu).基于傅里叶和小波变换的电网谐波分析(Power harmonic analysis based on Fourier and wavelet transform)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2005，17(6)：59-62，99.

[2] (美)小贾尔斯·伯吉斯.管制和反垄断经济学[M].上海: 上海财经大学出版社，2003.

[3] 布莱赫特 R E.数字信号处理的快速算法[M].北京: 科学出版社，1992.

[4] 殷福亮,宋爱军.数字信号处理C语言程序集[M].沈阳: 辽宁科学技术出版社，1997.

[5] (加)Blanchette J，(英)Summerfield M. C++ GUI Qt 4编程[M].北京: 电子工业出版社，2008.

[6] 易立强,邝继顺(Yi Liqiang, Kuang Jishun).一种基于FFT的实时谐波分析算法(FFT-based algorithm for real-time harmonic analysis)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(2):98-102.

HarmonicAnalysisofPowerSystemIntroducedHirschmanIndex

SU Guang-ning， YAN Zheng， DU Hao

(Key Laboratory of Control of Power Transimission and Transformation, Ministry of Ecluction,Department of Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Fast Fourier transform(FFT)is the most important method used in power system harmonic analysis.However,taking finite-duration signals makes i inaccuracy.In order to improve analysis accuracy,this paper presents a new algorithm based on the concept of Hirschman index(HHI) in the monopoly economics,which evaluates the intensity of frequency spectrun and gets the best sequence length to participate FFT.Good-Thomas algorithm is used to calculate random length sequence apace accurately.The data source is format Comtrade measuring in the on-site.The simulation results demonstrate the effectiveness of the proposed algorithm.Based on above algorithm,a harmonic analysis software of power system is accomplished using Qt,which is a kind of cross-platform programming language.

harmonic； fast Fourier transform； Hirschman index； sequence length

2009-09-25

2009-11-02

TM714

A

1003-8930(2011)01-0123-04

苏广宁(1986-)，男，硕士研究生，研究方向为电能质量。Email:realsgn@163.com 严 正(1964-)，男，教授，博士生导师，研究方向为电力系统优化运行、电力系统稳定分析、电力市场。Email:zhengyan_sjtu@yahoo.com.cn 杜 浩(1987-)，男，硕士研究生，研究方向为电能质量。Email:duhao@mail.sjtu.edu.cn