灵敏度法求取戴维南等效参数的静态电压稳定分析

李日波， 吴政球， 葛建伟， 刘 鼎， 朱文慧， 黄银华， 张 超

(1.湖南大学电气与信息工程学院， 长沙 410082； 2.衡阳电业局， 衡阳 421001)

灵敏度法求取戴维南等效参数的静态电压稳定分析

李日波1，2， 吴政球1， 葛建伟1， 刘 鼎1， 朱文慧1， 黄银华1， 张 超1

(1.湖南大学电气与信息工程学院， 长沙 410082； 2.衡阳电业局， 衡阳 421001)

在戴维南等效模型基础上提出了一种求戴维南等效参数的新算法。该方法利用节点分压原理在初始状态下和在有功功率扰动下列方程组。由于该方程组是线性的，解时不需要迭代，不需要传统算法的两点或者多点潮流数据，计算量小。在负荷节点进行戴维南等效，利用电压灵敏度求得戴维南等效参数以后，利用阻抗模裕度和负荷裕度指标进行了静态电压稳定性分析。在IEEE-30和IEEE-57节点系统验证了该方法的正确性和有效性。

电力系统； 灵敏度法； 戴维南等效； 静态电压稳定； 稳定分析

21世纪以来，随着世界经济的发展和人民生活水平的提高，电力需求也随之高涨。电力需求的迅猛增长对电力系统的稳定也提出了挑战，近年来陆续发生的电压失稳就是例证，电压稳定问题的研究变得严重突出[1，2]。

电力系统静态电压稳定性分析一般是基于潮流方程或者扩展潮流方程的[3，4]，其中利用电网戴维南等效计算近年成为一个研究热门。由于戴维南等效计算模型简单，在静态电压稳定性分析中应用广泛，成为电力系统电压稳定研究的一项重要课题。P.Kessel在文献[5]提出了负荷功率达到最大值的条件是负荷阻抗模值与戴维南等效阻抗模相等。如果能准确跟踪戴维南等效参数的变化就能知道负荷节点的静态电压稳定临界点。文献[6]运用戴维南等效方法求取戴维南等效基础上计算电压稳定性极限。文献[7～10]利用戴维南等效对电网进行了电压稳定性分析。本文在利用潮流计算方法求得基态下的潮流解，结合相关灵敏度算法和相关文献[11，12]，利用节点电压的实部和虚部对有功功率的灵敏度求取戴维南等效参数，利用阻抗模裕度和负荷裕度对标准节点系统进行了静态电压稳定性分析。这种方法求解速度很快，给电网调度人员提供即时的可靠信息和对当前电网一个直观的判断，可以作为电网调度中心的一种监控工具。

1 求取戴维南等效参数的方法

1.1 模型的建立

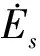
图1 戴维南等效电路图

1.2 戴维南等效参数计算

系统在正常状态下时，根据图1戴维南等效电路中的模型可知，对某一母线节点有：

(1)

将(1)式展开分离实部和虚部可以得到：

f1(es，fs，Rs，Xs)=XLfs+eLRs+eLRL-

fLXs-fLXL-RLeS=0

(2)

f2(es，fs，Rs，Xs)=fLRs+eLXs+eLXL+

fLRL-XLes-RLfs=0

(3)

式(2)和(3)中负荷阻抗可以通过潮流计算得到的节点电压和功率求得，含有的4个未知数必须需要四个方程才能求解。故还需要两个方程才能求取戴维南等值内电势和内阻抗的值。

系统在受扰动状态时，负荷节点处受到有功扰动为图2。

图2 有功功率扰动图

如图2，假如节点负荷给一个有功功率扰动为ΔPL，对应的电阻值为ΔRL，此时可以视电路其余部分、原负荷阻抗与扰动电阻并联。根据电路分压原理有：

(4)

用直角分量代入，展开式(4)的实部和虚部得：

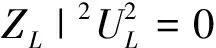
(5)

(6)

如果将负荷节点电压的实部和虚部均看做负荷节点处扰动功率的函数。如果ΔPL→0，式(5-6)中的节点电压实部和虚部分别对扰动功率求导，得到参数求取的另外两个方程：

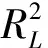
(7)

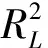
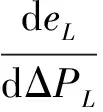
(8)

下面求出式(7)和(8)中的电压实部和虚部对有功微增量的导数。

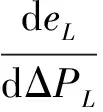
(9)

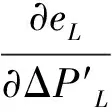
下面给出求4个原始灵敏度的计算方法。

用牛顿拉夫逊法求解潮流时，在直角坐标下，其修正方程式为

-J[ΔU]=[ΔW]

(10)

其中，J为潮流雅可比矩阵，[ΔU]为牛顿迭代过程中的电压实部和虚部变化量，[ΔW]为有功功率偏差量、无功功率偏差量和电压平方偏差量。解上述潮流得到所研究等值节点的电压实部eL和它的虚部fL。

(11)

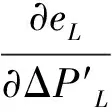
利用(2～3)、(7～8)式构成线性方程组可快速求解戴维南等效参数。

1.3 静态电压稳定性研究

目前电压静态稳定分析指标很多,比如灵敏度指标，特征值、奇异值指标，负荷裕度，VIPI指标，能量函数指标，本文采用阻抗模裕度和负荷裕度来计算分析。

戴维南等值阻抗ZS就是对应该节点的临界阻抗模。阻抗模指标定义为

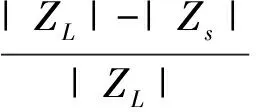
(12)

阻抗模裕度γ的取值在节点电压稳定情况下为0到1，阻抗模裕度越小，表明电压稳定裕度越小。随着γ值的减小，电压稳定程度越低，当γ等于0时，即ZL和Zs的模值相等，节点电压达到稳定极限。利用上述方法对每个负荷节点进行分析，阻抗模裕度γ最小的节点为网络电压稳定性最薄弱的节点。

负荷裕度计算方法如下：为了简化计算，利用极坐标简化。设节点k戴维南等效内电动势为Ek∠0°，戴维南等效阻抗为Rk+jXk，节点电压为Uk∠δ，负荷功率为Pk+jQk。该参数根据上述灵敏度方法求出。由分压原理推出：

Ek-(Ukcosδk+jUksinδk)=

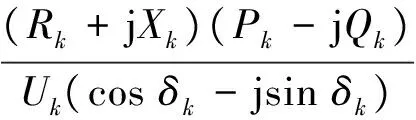
(13)

上式变形分离实部和虚部得到：

(14)

EkUksinδk=PkXk-QkRk

(15)

联立以上两式，消去功角得到：

(16)

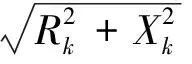
(17)

(18)

(19)

式中，N为系统的负荷节点总数。系统负荷的增加，电压崩溃肯定最先发生在负荷裕度最小的负荷节点上。

应当注意的是，用戴维南等效参数求解节点k最大负荷裕度的过程中，可能出现无功越限的现象，可将该最大负荷裕度缩至98%后再解潮流方程，直至有解，满足各种潮流有解的约束条件，此时的负荷裕度为最大负荷裕度，误差很小。

2 算例分析

下面用IEEE-30节点和IEEE-57节点对本文所提算法进行验证分析，由于篇幅有限，只列出部分结果。

IEEE-30节点系统有24条负荷母线，只列出了3、7、10、12、18、19、21、23、26、30号节点数据，包括节点等效电压、节点等效阻抗，节点等效阻抗模值和节点阻抗模裕度量，见表1。

表1 IEEE-30节点系统的负荷节点戴维南等效参数及静态电压稳定裕度(标幺值)

由表1中看出，阻抗模裕度较小的有21、26、30号节点，尤其是30号节点的阻抗模裕度小于其他所有节点的裕度，为电压稳定性最薄弱的节点。

IEEE-57节点系统中负荷节点很多，本文只选取其中5、10、14、18、20、23、29、35、38、42、49、53、55、57号节点作为研究对象，见表2。

表2 IEEE-57节点系统的负荷节点戴维南等效参数及静态电压稳定裕度(标幺值)

从表2可以看出，节点18、42、53的阻抗模裕度比较小，即为电压稳定性较小的弱负荷节点，其中53号节点的阻抗模裕度最小。

表3列出了用本文方法计算的负荷裕度与连续潮流计算的结果，偏差很小，验证了本文算法的准确性。

表3 IEEE-30节点系统和IEEE-57节点系统的负荷裕度

3 结语

本文提出了一种计算戴维南等效参数的新方法。在系统基态和有功扰动状态分别列节点电压方程组，该方程组是四维线性方程组，求解方便。在IEEE-30和IEEE-57节点系统上对负荷节点进行了戴维南等效求取参数，然后利用指标进行了电压稳定性分析，验证了该方法的正确性。此方法简单快速，可以为电力调度人员提供快速、直观的电压稳定裕度，可做为调度中心静态电压稳定性的监控工具。

[1] Counan C,Trotignon M, Corradi E. Major incidents on the French electric system potentiality and curative measures studies[J]. IEEE Trans on Power Systems,1993,8(3)：879-886.

[2] 印永华，郭建波，赵建军，等(Yin Yonghua,Guo Jianbo,Zhao Jianjun,etal). 美加“8.14”大停电事故初步分析以及应吸取的教训(Preliminary analysis of large scale blackout in interconnected north America power grid on August 14 and lessons to be drawn)[J].电网技术(Power System Technology)2003,27(10)：8-11,16.

[3] 张尧，张建设，袁世强(Zhang Yao,Zhang Jianshe,Yuan Shiqiang).求取静态电压稳定极限的改进连续潮流法(Improved continuation power flow algorithm for obtaining the limit of static voltage stability)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2005，17(2)：21-25.

[4] 张勇军，陈扬华，任震，等(Zhang Yongjun,Chen Yanghua,Ren Zhen,etal).计及电压稳定的最优潮流综述(Survey on optimal power flow considering voltage stability)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2008，20(4)：17-22.

[5] Kessel P, Glavitsch H. Estimating the voltage stability of a power system[J].IEEE Trans on Power Delivery,1985,1(3)：346-354.

[6] Haque M H. Fast method for determining the voltage stability limit of a power system[J].Electric Power System Research,1995,32(1)：35-43.

[7] 邱晓燕，李兴源，王建，等(Qiu Xiaoyan,Li Xingyuan,Wang Jian,etal).电力系统实时等值及电压稳定性分析(Power system equivalent in real time and voltage stability analysis)[J].电网技术(Power System Technology)，2004，28(7)：7-9,48.

[8] 段俊东，郭志忠(Duan Jundong,Guo Zhizhong).一种可在线确定电压稳定运行范围的方法(A new method for on-line determination of capability curves of voltage stability)[J].中国电机工程学报(Proceedings of the CSEE)，2006， 26(4):113-118.

[9] 李来福，柳焯(Li Laifu,Liu Zhuo).基于戴维南等值参数的紧急态势分析(Urgent situation analysis base on Thevenin equivalent parameters)[J].电网技术(Power System Technology)，2008，32(21)：63-67.

[10]刘明松，张伯明，姚良忠，等(Liu Mingsong,Zhang Boming,Yao Liangzhong,etal).基于PMU和改进戴维南等值模型的电压稳定在线监视(On-line voltage stability monitoring based on PMU and improved Thevenin equivalent model)[J].电力系统自动化(Automation of Electric Power system)，2009，33(10)：6-10.

[11]邓阳，吴政球，容文光，等(Deng Yang,Wu Zengqiu,Rong Wenguang,etal). 基于泰勒级数的N-1网络快速灵敏度修正计算(Sensitivity of N-1 system fast correction calculation based on Taylor series)[J].继电器(Relay)，2007，35(16)：23-26.

[12]罗华伟，吴政球，戴庆华，等(Luo Huawei,Wu Zhengqiu, Dai Qinghua,etal).电网戴维南等值参数的快速计算(Fast computation of Thevenin equivalent parameters)[J].中国电机工程学报(Proceedings of the CSEE)，2009，29(1)：35-39.

AnalysisforStatic-stateVoltageStabilityBasedonObtainingTheveninEquivalentParameterswithSensitivityMethod

LI Ri-bo1，2， WU Zheng-qiu1， GE Jian-wei1， LIU Ding1ZHU Wen-hui1， HUANG Yin-hua1， ZHANG Chao1

(College of Electrical and Information Engineering，Hunan University，Changsha 410082，China)

A new algorithm of calculating Thevenin equivalent parameters is proposed based on Thevenin equivalent's model. Making use of node voltage partial pressure principal both on initial status and active power disturbance status, equations set can be listed. This equations set is linear, which can be sloved without iterating and flow datas of two or more points as conventional algorithm. It is less computation. After using Thevenin's equivalent on load nodes and gaining Thevenin equivalent parameters by using voltage sensitivity, stability analysis of static-state voltage is proceeded by using resistance module margin and load margin indicators. Tests on IEEE 30-bus and IEEE 57-bus systems verify the correctness and practicability of this method.

power system； sensitivity method； Thevenin equivalent； static-state voltage stability； stability analysis

2010-05-23；

2010-06-17

TM711

A

1003-8930(2011)06-0076-05

李日波(1983-)，男，硕士研究生，研究方向为电力系统电压稳定性。Email:tyliribo12@163.com 吴政球(1963-)，男，博士，教授，博士生导师，研究方向为电力系统运行分析与控制、电力市场与分布式发电及相关技术。Email:zhengqiuwu@163.com 葛建伟(1985-)，男，硕士研究生，研究方向为电力系统电压稳定性。Email:gejianwei2008@163.com