大型同步发电机非线性最优预测综合控制

蒋铁铮

(长沙理工大学电气工程学院， 长沙 410114)

大型同步发电机非线性最优预测综合控制

蒋铁铮

(长沙理工大学电气工程学院， 长沙 410114)

针对静止励磁方式和电液调速系统的汽轮发电机组，基于多输入多输出非线性预测控制理论，设计出具有解析解控制律的汽轮发电机非线性预测综合控制器。该设计方法避免了非线性预测控制在线优化带来的巨大计算负担及由此产生的控制算法的稳定性问题。控制器的输入均为当地可测信号且与网络参数无关，设计参数只有滚动预测时间及控制阶。仿真结果表明，该控制器对提高电力系统稳定性和维持机端电压调节精度是有效的。

多输入多输出非线性系统； 预测控制； 电力系统稳定性

提高系统稳定性与满足发电机机端电压调节精度是两个相互矛盾的控制目标，如果改善电压调节特性，那么功角稳定的动态特性就会变坏，反之亦然。显然，把这两个相互矛盾的控制目标都由励磁系统来实现，其控制效果必将受到影响。近年来，由于调速系统的数字化，其惯性时间常数已大大减小，为通过调速系统直接抑制有功功率的振荡提供了可能，且对励磁与调速系统的协调控制研究已取得许多成果[1～5]。富士公司基于线性多变量最优控制理论，开发了发电机多变量综合控制器，简称为TAGEC(total automatic generation controller)[6]。该控制器使发电机的励磁与调速控制系统集于一体，以利于提高系统稳定性。

电力系统是一个典型的非线性系统，对其完整准确建模并获得精确的模型参数是不切实际的。预测控制只需一个具有预测功能的模型，避免了对其完整建模和参数准确性的困难，同时，预测控制以滚动的有限时域优化取代经典最优控制中一成不变的全局优化，能够不断利用由不确定因素引入系统的新信息对预测结果加以校正，达到比依靠模型进行一次优化的传统优化算法更为优越的控制效果，具有更强的鲁棒性[7]。但非线性预测控制算法在线滚动优化的巨大数值计算负担及由此产生的控制算法稳定性问题是阻碍这一先进控制理论在电力系统应用的主要障碍。所以，预测控制在电力系统的应用研究大都是基于线性化模型来实现的[8～11]。

针对具有不同关系度的多输入多输出仿射非线性系统，本文设计了一种具有解析解控制律的发电机励磁和主汽门开度综合控制器。该综合控制器不需进行在线优化计算，避免了巨大的计算负担和由此带来的控制算法稳定性问题。

1 多机电力系统数学模型的建立

考虑n台发电机互联电力系统，发电机采用计及励磁系统动态经典三阶模型，则第i台发电机的数学模型为

1.1 转子运动方程

(1)

(2)

1.2 电磁暂态方程

(3)

1.3 电气方程

(4)

Efi=Kciufi

(5)

(6)

(7)

(8)

(9)

(10)

(11)

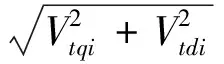
(12)

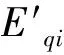
1.4 汽机调速系统的动力学方程[12，13]

考虑到再热器的时间常数TR(大约10～20 s) 一般远大于电力系统暂态过渡过程所经历的时间，所以对于中间再热式汽轮机组，主要以高压主调节汽门为受控对象，并假定中间调节汽门不参与调节，即中低压缸输出的机械功率PML不变，PML≡PML0，则其动力学方程可表示为

(13)

Pmi=PHi+PMLi

(14)

PHi=CHiPmi

(15)

PMLi=PMLi0=CMLiPmi0

(16)

式中：CHi为高压汽缸功率分配系数，约为0.3；CMLi为中、低压汽缸功率分配系数，且满足CHi+CMLi=1；THΣi为高压汽缸等效时间常数，约为0.4；ui为高压缸调节汽门开度。

1.5 状态变量的选择

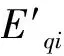
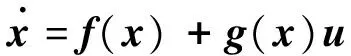
(17)

这里

f(x)=

式中：

其中，x=[Δωi，ΔPei，ΔPmi，ΔVti]T，u=[Efi，u1i]T分别是状态矢量和控制矢量。

1.6 输出函数的选取

当电力系统由于故障或其它原因进入暂态过渡过程时，必然导致发电机转轴上的功率不平衡，即ΔPei≠0，使发电机处于加速或减速，即Δωi≠0，导致发电机功角δi偏移和机端电压Vti变化，从而使系统失稳或振荡。综合控制器的作用就是通过有效地控制发动机组的励磁和汽轮机主汽门开度，使系统尽快达到稳态，即满足Δωi=0，ΔVti=0。因此，Δωi=0，ΔVti=0可设为预测控制中参考轨线的设定点。由此，跟踪目标即参考轨线W(t)可选定为Δωi，ΔVti，则输出函数可由式(18)给出。

yi1(t)=hi1(x)=Δωi

yi2(t)=hi2(x)=ΔVti

(18)

2 具有不同关系度的多输入多输出非线性系统的预测控制器的设计方法

2.1 考虑多输入多输出仿射非线性系统

y1=h1(x)

…

ym=hm(x)

(19)

式中：f，gi∶Rn→Rn是光滑向量场；x=[x1，…，xn]T∈Rn为状态向量；ui(i=1，…，m)为控制量；yi(i=1，…，m)为输出量；hi(x)∶Rn→R的光滑函数。

对系统(19)作如下假设：①零动态是稳定的；②所有的状态变量是可用的；③输出yi(i=1，…，m)与参考轨线Wi(i=1，…，m)对时间t连续充分可微。

2.2 滚动优化性能指标

为了避免非线性最优控制需求解偏微分方程的困难，非线性预测控制采取一种滚动闭环优化控制算法，它是通过某一性能指标的最优来确定未来的控制作用，以达到非线性系统式(19)的输出yi(t)依据给定的性能指标最优地跟踪期望的参考轨线W(t)。因此，在任一时刻t起未来有限的时段T，滚动优化性能指标可表示为

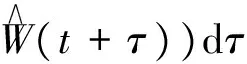
(20)

2.3具有不同关系度ρ={ρ1，ρ2，…，ρm}的多输入多输出非线性系统的模型预测控制算法

式(19)所示的多变量非线性系统，若每一个输出yi=hi(x)对应有不同的子关系度ρi，当给定一个控制阶r时，任一输出yi可用Taylor级数展开到ρi+r阶，则具有解析解形式的非线性预测控制律能唯一给出[14]：

u(t)=

(21)

式中：

A(x)=

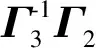
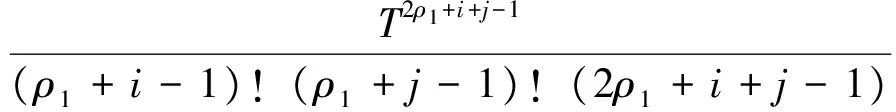
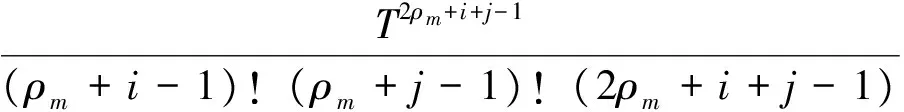
矩阵Γ2的第ij块的第j行由下式给出，第ij块的其余行的元素均为0。

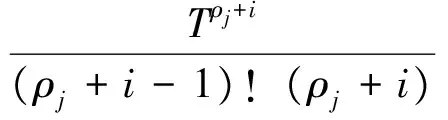
i=1，…，r+1，j=1，…，m(设计参数：r和T的选取原则可参文[15])

3 多机系统汽轮发电机综合控制器设计

依据式(17)、(18)求得其关系度为ρ={2，1}。

若取控制阶r=0，可导出汽轮发电机组的励磁和汽门开度的控制律：

(22)

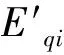
(23)

电流Idi，Iqi可由式 (8) 及式 (9)确定。即

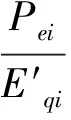
(24)

(25)

由此，综合控制器的所有输入信号仅是当地发电机的可测量(Pei、Qei、Vti、Δωi)，且与输电线路参数无关，因而对输电线路拓扑结构的改变具有很好的适应性和鲁棒性。

4 仿真计算结果与分析

为验证本文综合控制器的有效性，利用加拿大Powertech Labs公司的TSAT软件在图1所示的多机电力系统上进行仿真计算，其中6号机是调相机，1号机是参考机，分别在2号机到5号机安装传统的AVR励磁调节器、PSS及PID调速器(参数见文[16])和本文综合控制器(控制器设计参数均选取：控制阶r=0和预测时间周期T=0.5 s)。

在t=0.1 s时，系统在母线11与12间的线路上发生三相对地短路，故障点距母线11为10%线路长度处。在t=0.25 s时，故障线路被跳开；在t=0.8 s时线路重合闸成功。图2～5分别给出了各机组在传统控制和综合控制器作用下的动态响应曲线。

图2～5中发电机组的励磁电压及机端电压响应曲线表明，本文控制策略具有更好的机端电压调节精度。这一点可从控制励磁控制律Efi(式(22))得到很好的解释。为分析简单清楚起见，不考虑发电机定子绕组电阻Ra，认为其近似为0，则Gii≈0。于是式(22)的Efi可改写为

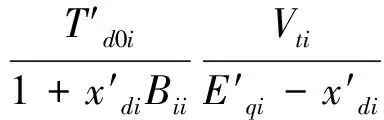
(26)

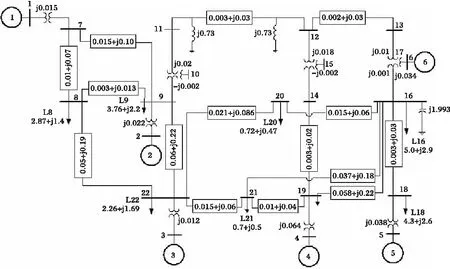
图1 多机电力系统结构图

(a) 2#机组功角响应曲线

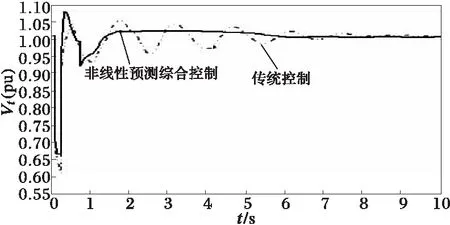
(b) 2#机组机端电压响应曲线

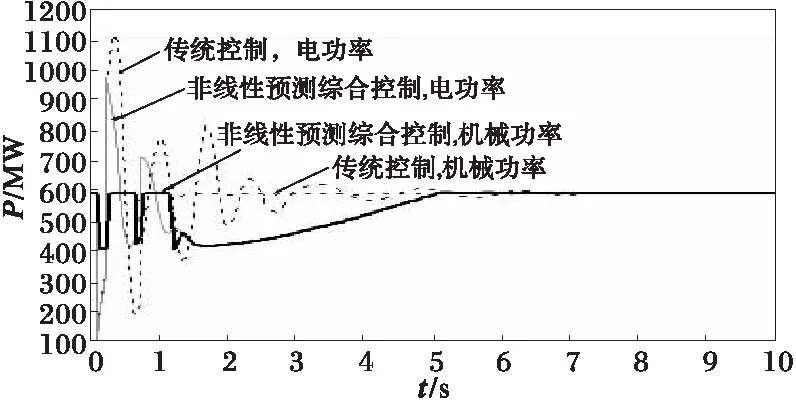
(c) 2#机组电功率和机械功率

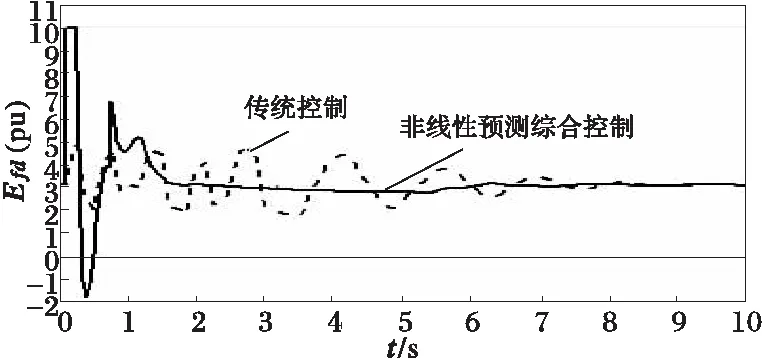
(d) 2#机组励磁电压

(a) 3#机组功角响应曲线

(b) 3#机组机端电压响应曲线

(c) 3#机组电功率和机械功率

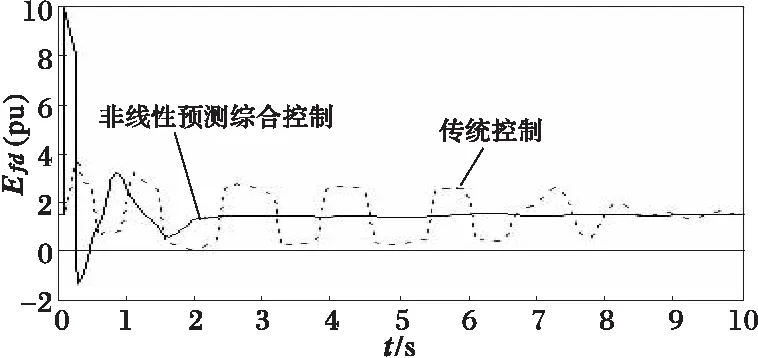
(d) 3#机组励磁电压

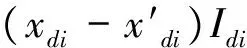
如图2～5中功角、电磁功率及机械功率响应曲线所示，本文的控制策略能对发电机功角的第一摆有很好的抑制作用，使第一摆功角δmax的值较传统控制方案减少(以2#机组为例，在传统控制方案和本文控制方案下，功角第一摆的最大值分别为δmax=70.73°与δmax=44.36°)，显然有利于暂态稳定性的提高。对机组的动态稳定也表现有很好阻尼作用，使系统尽快达到稳定状态。这可从图中各机组的机械、电气功率变化曲线得到说明，当发生故障时，发电机输出的电磁功率Pei将急剧减少，采用本文提出的控制器来调节主汽门开度，可有效地使发电机的机械输入功率减少，从而使发电机转子获得的加速功率减少，则功角δi的最大偏移将减小，提高了其暂态稳定性。随后，由于输入的机械功率能很好跟随发电机输出的电磁功率的变化，从而有效地阻尼了系统功率振荡，使系统尽快进入稳定状态。这得益于发电机组汽门开度的控制充分利用了当地机组丰富的变量信息，远优于传统调速系统控制器的单一转速增量Δωi作为控制输入信息。

(a) 4#机组功角响应曲线

(b) 4#机组机端电压响应曲线

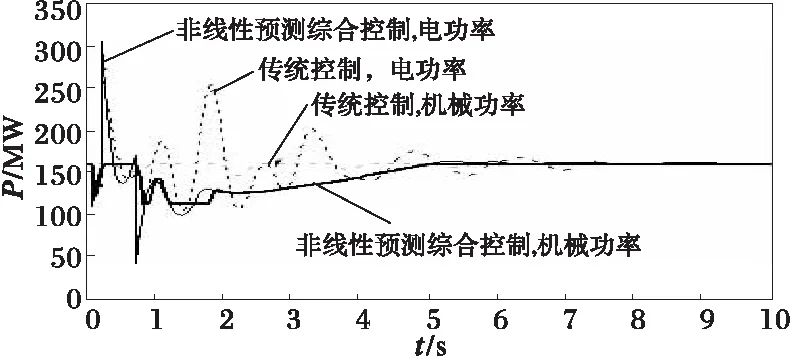
(c) 4#机组电功率和机械功率

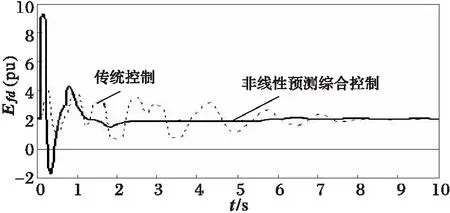
(d) 4#机组励磁电压

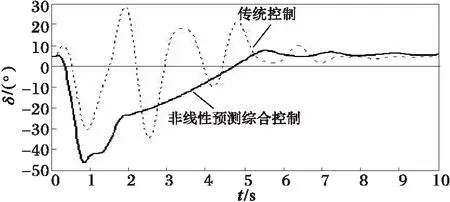
(a) 5#机组功角响应曲线

(b) 5#机组机端电压响应曲线

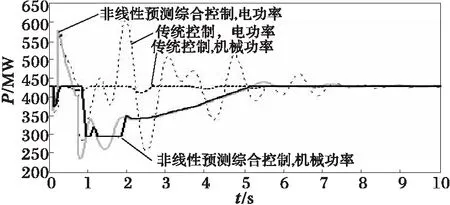
(c) 5#机组电功率和机械功率

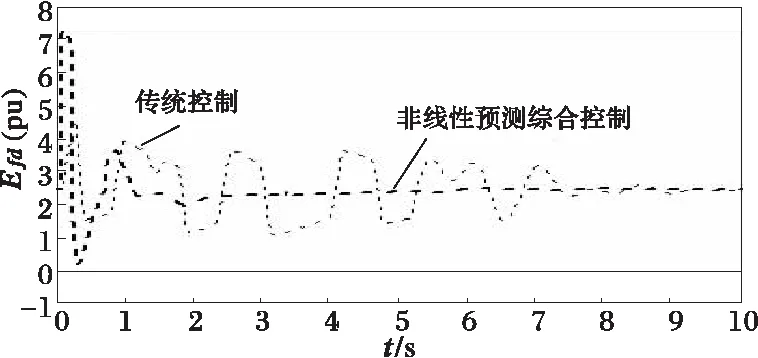
(d) 5#机组励磁电压

5 结语

针对对具有静止励磁方式和电液调速器的中间再热式汽轮发电机组，本文设计一种具有解析解控制律的发电机综合控制器。该控制器避免了非线性预测控制需在线滚动优化计算带来的大量计算负担和由此引起算法的稳定性问题，且控制器所有输入信号都是当地测量的，可实现分散控制。通过对一多机电力系统的仿真结果表明，与传统AVR励磁调节器、PSS及PID调速器相比，该综合控制器能有效地提高系统的暂态稳定性并能得到更好的动态响应特性和维持机端电压的调节精度。

[1] Guo G, Wang Y，Lim K Y,etal. Robust nonlinear controller for power system transient stability enhancement with voltage regulation[J]. IEE Proceedings: Generation, Transmission and Distribution, 1996, 143(5): 407-412.

[2] 葛友，李春文，孙政顺(Ge You, Li Chunwen, Sun Zhengshun)．逆系统方法在电力系统综合控制中的应用(Application of inverse system method for power system integrated control)[J]. 中国电机工程学报(Proceedings of the CSEE), 2001,21(4):1-4,10.

[3] 王冰，季海波，陈欢，等(Wang Bing, Ji Haibo, Chen Huan,etal).汽轮发电机励磁与汽门协调无源性控制(The coordinated passivity techniques for the excitation and steam-valving control of generator)[J]. 中国电机工程学报(Proceedings of the CSEE), 2004,24(5):104-109.

[4] 戴先中，张腾，张凯锋, 等(Dai Xianzhong, Zhang Teng, Zhang Kaifeng,etal). 发电机励磁与汽门系统解耦控制的神经网络逆系统方法(Ann-inverse based decoupling control of excitation and valve system for turbogenerator )[J]. 中国电机工程学报(Proceedings of the CSEE), 2002,22(11):75-80.

[5] 李志民，卢曦，孙勇，等(Li Zhiming, Lu Xi, Sun Yong,etal).同步发电机云模型励磁控制器的设计(Design of cloud model excitation controller for synchronous generator) [J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2010,22(3): 91-95.

[6] 李基成.现代同步发电机励磁系统设计及应用[M].北京: 中国电力出版社，2002.

[7] 王伟．广义预测控制理论及其应用 [M].北京: 科学出版社, 1998.

[8] Barreiros J A L, e Silva A S, Simoes Costa A J A. A self-tuning generalized predictive power system stabilizer[J].International Journal of Electrical Power and Energy System, 1998, 20(3): 213-219.

[9] Ghazizadeh M S, Saidy M, Hughes F M. Predictive analogue generator excitation controller[J]. IEE Proceedings: Generation, Transmission and Distribution, 1997, 144(3): 271-278.

[10]Marinescu Bogdan, Bourles Henri. Robust predictive control for the flexible coordinated secondary voltage control of large-scale power systems[J]. IEEE Trans on Power Systems, 1999,14(4): 1262-1268.

[11]Rajkumar V, Mohler R R. Bilinear generalized predictive control using the thyristor-controlled series-capacitor[J]. IEEE Trans on Power Systems, 1994,9(4): 1987-1993.

[12]卢强，孙元章.电力系统非线性控制 [M]．北京: 科学出版社，1993．

[13]Kundur P. Power System Stability and Control [M]. Beijing: China Electric Power Press, 2001.

[14]Chen Wen-Hua. Closed-form nonlinear MPC for multivariable nonlinear systems with different relative degree[C]∥The American Control Conference, Denver, USA: 2003.

[15]Chen Wen-Hua, Ballance Donald J, Gawthrop Peter J. Optimal control of nonlinear systems: a predictive control approach [J]. Automatica, 2003, 39(4): 633-641.

[16]Lu Qiang, Sun Yuanzhang, Mei Shengwei. Nonlinear Control Systems and Power System Dynamics[M]. Boston: Kluwer Academic Publishers, 2001.

DesignedofNonlinearOptimalPredictiveIntegratedControlforTurbine-generator

JIANG Tie-zheng

(College of Electrical Engineering， Changsha University of Science and Technology， Changsha 410114， China)

A nonlinear integrated controller with analytic solution control regulation for turbine-generators with static excitation and electric-hydraulic transducer is presented, on the basis of multi-input multi-output (MIMO) nonlinear predictive control theory. The advantage of the control scheme is no requirement for on-line optimization, thus the huge calculation burden and control arithmetic stability can be avoided, so demanding of real-time control can be satisfied. The input signals for the proposed controller are local measured and independent of the system parameters, and two design parameters which are the predictive period and control order. The simulation results of a multi-machine power system have shown that the controller can greatly improve power system stability and maintain terminal voltage of turbine-generators.

multi-input multi-output nonlinear system； predictive control； power system stability

2010-08-24；

2010-11-11

湖南省教育厅资助科研项目(08C086)

TM761

A

1003-8930(2011)06-0029-07

蒋铁铮(1965-)，男，博士，副教授，研究方向为电力系统稳定分析与非线性控制。Email:jiangtiezheng@163.com