三次方程根的判别式定理的新证明

陈海燕

（盐城师范学院 数学科学学院，江苏 盐城 224002）

1 问题的提出

对于实系数的一元三次方程

初等数学研究中给出其解的基本思路是通过作差根变换

将其化为不完全三次方程

形式来解，并运用特殊的技巧方法给出了方程

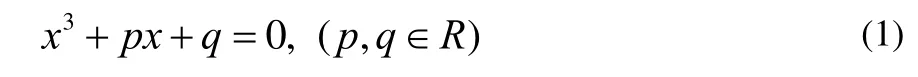
的根的公式

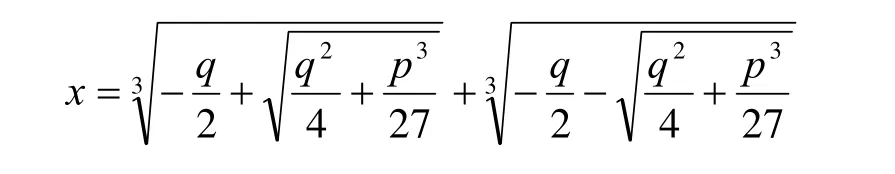
该公式通常称为卡丹（Cardano）公式，并由卡丹公式及其推导过程可得到方程(1)的根的判别式定理。

定理（三次方程根的判别式定理）对于一元不完全三次方程

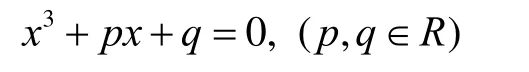
其判别式为

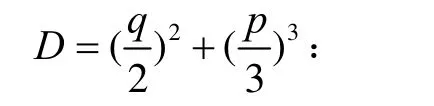
（1）D＞0，方程有一个实根和一对共轭虚根；

（2）D=0，方程有三个实根，且其中有两个相等；

（3）D＜0，方程有三个互不相等的实根。

易见三次方程 x3+px+q= 0(p,q ∈R )根的判别式D与 一 元 二 次 方 程 ax2+bx+c= 0(a≠0)根 的 判 别 式Δ= b2- 4ac的作用相同。由于三次方程根的判别式定理需要借助于卡丹公式的推导过程才能理解透彻（参见文献[1]和[2]），而卡丹公式的推导技巧性又较强，所以，要深刻理解D的符号如何对三次方程的根的影响不如一元二次方程根的判别式那么直观。为此，我们利用高等数学的相关知识给出三次方程根的判别式定理一个新的证明，从中能较直观地看出D的符号如何影响三次方程根的情况。

2 一元不完全三次方程根的判别式定理的新证明

根的存在性定理[3]若函数 f(x)在闭区间[a,b]上连续，且 f(a)f(b) ＜ 0，则至少存在一点 c∈ (a,b)，使得f(c) = 0。

下面我们证明三次方程根的判别式定理。

证明易见，D＞0当且仅当p＞0或p=0，q≠0或p＜ 0，并且（其中 p1=(- p /3)1/2，下同）；

设f(x )= x3+ px + q ，则f(x)在实数域R上连续可导，且 f′(x) = 3x2+ p。

（1）若 p＞0，则 f′(x)＞0，从而 f(x)在实数域R上严格递增。此时， f(x)图象与x轴至多有一个交点。又因为，所以，存在[a,b]⊂ R，使得 f(a)＜0，f(b)＞0。由根的存在定理知f(x)图象与x轴有且仅有一个交点，即方程f(x)=0恰有一实根。再由高等代数中实系数一元多项式分解定理[4]易知，多项式x3+px+q可分解为一次因式和二次不可约因式的积。由此可知方程f(x)=0有一个实根和一对共轭虚根。

（2）若p=0，则 f(x)有唯一稳定点x0=0，除此以外的任一点x，有 f′(x)＞0。此时，若q≠0，则同（1）可推知方程 f(x)=0有一个实根和一对共轭虚根；若q= 0，则方程f(x)=0即为x3=0，该方程有三重根。

容易算出

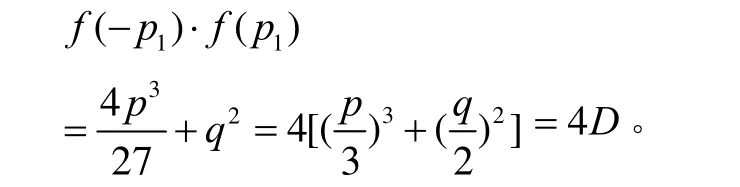
又

综上可得出定理的结论。

从以上证明可以看出，当p＜0时，D的符号即为f的两个极值的乘积的符号。当D＞0时，函数f(x)的图象如图1，当D=0、D＜0时，图象分别如图2、3。

图1 (a) D>0

图1 (b) D>0

图2 D=0

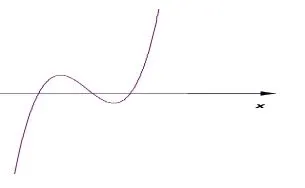
图4 D<0

从而不难理解D的符号对不完全三次方程

根的影响。这一点在初等数学研究的相关证明中难以看出。