矩阵变换的若干应用

向 伟

（重庆师范大学 数学学院，重庆 400047）

矩阵是代数特别是高等代数的主要研究对象。当今国内外有许多学者致力于这方面的研究并且取得了一定的成就。他们均是站在数学发现和发展的高度，分别从矩阵的初等变换概念、性质及矩阵的初等变换在研究矩阵的行列式、秩、特征值和特征向量、求矩阵的逆（包括λ矩阵的逆）、求向量组 a1,a2,… ,as的极大无关组、求标准正交基、求解矩阵方程与线性方程组等方面的应用，还对得出的这些结论作了系统的证明。本文探讨矩阵初等变换在多项式方面和向量组方面的应用。

矩阵A的初等变换是指对矩阵实施以下三种变换：

（ⅱ）用一个不为零的数k乘矩阵A的某一行（列）的所有元素（用k×ri表示用k乘第i行，用 k× ci表示用k乘第i列）；

（ⅲ）把矩阵A的某一行（列）的所有元素的k倍加到另一行（列）的对应元素上去（用 ri+k×rj表示将第 j行乘以k再加到第i行，用 ci+ k × cj表示将第j列乘以k再加到第i列）。

文中所涉及到的矩阵的乘法和加法都假定是可乘和可加的。

1 在多项式中的应用

引理1若，则

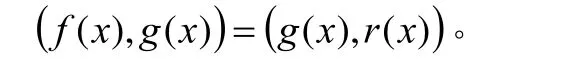
即，若

则

由此可见，对多项式矩阵

施行初等行变换，不会改变f(x)，g(x)的最大公因式，且当多项式矩阵

经初等行变换化为

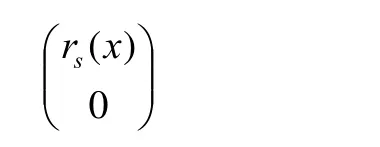
就转化为“系数矩阵”

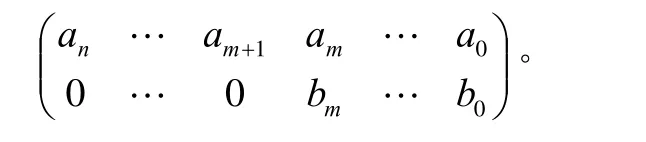
于是，对

施行一次初等行变换消去f(x)的最高次项，相当将矩阵

的第二行乘以 - an/bm后向左移动n-m位加到第一行（称为错位初等行变换）。

引理2若

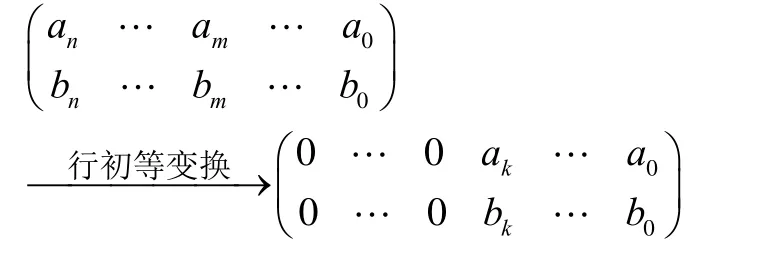
则

与

对应的多项式的最大公因式相同。

综上所述，可得用矩阵的初等变换求两个多项式f(x)，g(x)的最大公因式的方法：

（1）给出多项式矩阵

对应的 “系数矩阵”

（2）对A施行错位初等行变换，当前面若干列全为 0时，可将这些列去掉，直到将其化为

的形式为此。

（3）d (x ) = csx5+…+ c0即为多项式 f (x),g(x)的一个最大公因式。

例 1求 f(x) = 3 x3- x2- x -1， g(x) = 6 x4+ 4 x3+ 5x2+2x+1的最大公因式。

解作它们的系数矩阵

对A施行错位初等行变换

故d(x)=3x2+ 2x +1为所求的一个最大公因式。

也可将这种方法推广到求多个多项式的最大公因式的问题上去。

例2求的最大公因式d(x)。

解

定理1设多项式矩阵

经过初等行变换化为

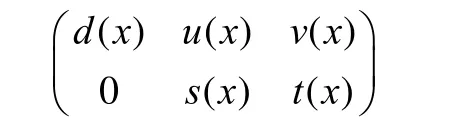
则d(x)=u(x)f(x)+v(x)g(x)，且d(x)为 f(x)与g(x)的最大公因式。

定理2设多项式矩阵

经过初等行变换化为

例 3设 f(x)=x3+x2， g(x) = x2+ 2 x+1，求它们的最大公因式d(x)，并求出u(x)，v(x)，使得d(x)=

解构造矩阵

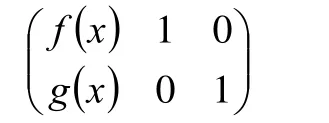
并作初等行变换，

定理3矩阵的行秩与列秩相等。

定理4线性相关的充分必要条件是齐次线性方程组有非零解。

定理5齐次线性方程组有非零解的充分必要条件是的系数矩阵

2 在向量组方面的应用

的行秩r＜n。

例 4已知α1=(1,1,1)，α2=(0,2,5)，α3=(1,3,6)，判断α1, α2,α3的线性相关性。

解以α1,α2,α3为列向量构造矩阵，并对其施行初等行变换

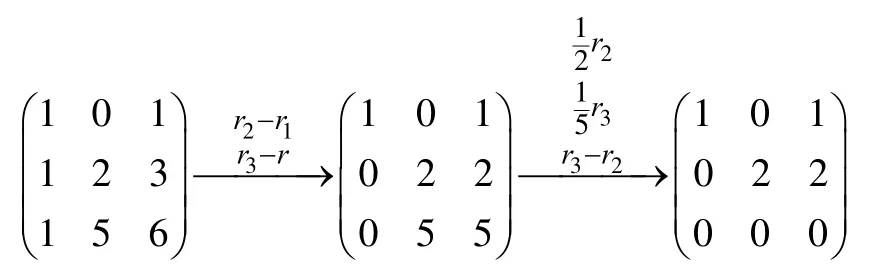
定理6设

与增广矩阵

有相同的行秩。

例 5已知向量组试判断β能否由α1,α2线性表出，若能，则写出相应的线性表达式。

解以α1,α2,β为列构成矩阵，并对它施行初等行变换，化为行最简阶梯形矩阵：

则r（ A）= r （A），且 β= 3α1- α2。

定理7设向量组以它们为列构成矩阵A 经过行初等变换化为阶梯型矩阵B，B的非零行的首个非零元所在的列对应的向量αi1,αi2,…,αir构成α1,α2, … ,αm的一个极大无关组，其向量的个数即为向量组的秩。

例 6利用矩阵初等变换求下列向量组的秩与一个极大无关组

解将已知向量为列构成4×5的矩阵A，并对它施行初等行变换

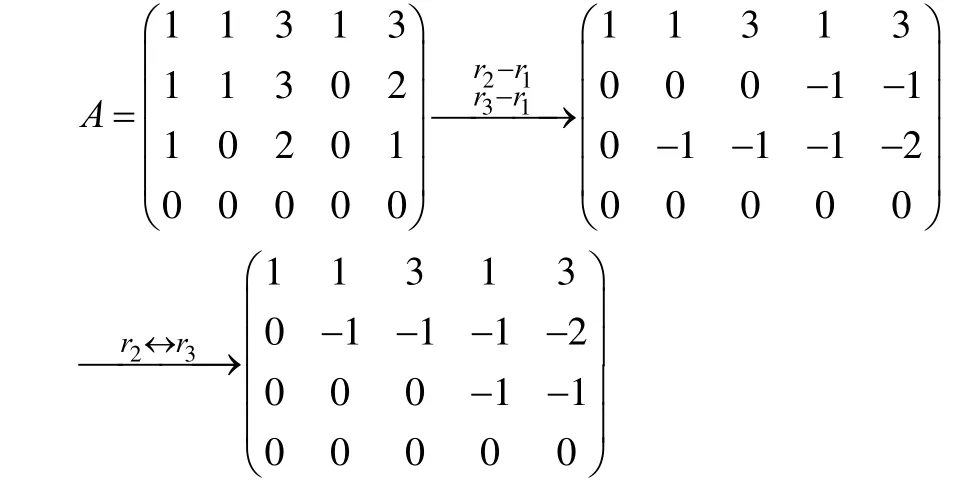
故α1, α2,α4为该向量组的一个极大无关组，且其秩为3。

已 知 向 量 组 α1,α2, …,αm与 β1, β2, … ,βs， 分 别 以为列构成矩阵A与矩阵B，令矩阵 C= （AB），则由性质 3知，矩阵的初等行变换不改变列向量间的线性相关性，故有：

定理8 α1,α2, …,αm与等价的充要条件是r(A) = r(B ) = r(C)。

例 7判断向量组α1=(1,2,-1,5)，α2= (2,-1,1,1)和向量组β1=(4,3,-1,11)，β2=(4,3,0,11)是否等价。

解由性质3知，矩阵的初等行变换不改变列向量间的线性相关性，故分别以α1，α2和β1，β2为列构成矩阵A，B，令 C= （AB ），然后对C施行初等行变换

定理9设W1，W2分别是由与 β1,β2，… ,βs生成的子空间，则

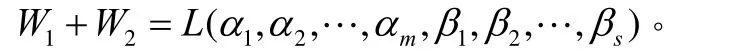
例10 求子空间 L (α1,α2)与 L (β1, β2)的和空间的基与维数，其中α1=(1,1,0,0)，α2=(1,0,1,1)，β1=(0,0,1,1)，β2=(0,1,1,1)。

解以为列构成矩阵A，对A施行初等行变换，使它化为行最简形矩阵B

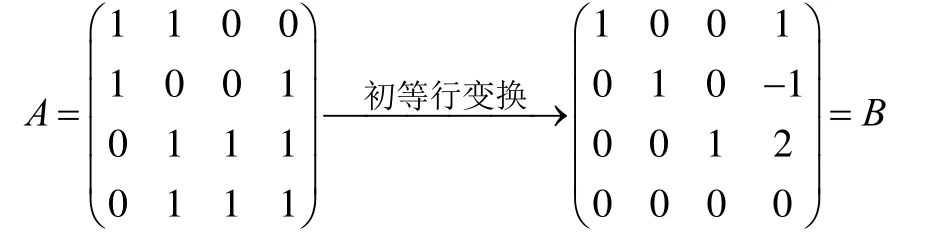
由B可得，α1，α2是L (α1,α2)的一组基，且

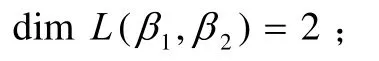
α1，α2，β1是

的一组基，且