人民币汇率与地产行业间的联动关系研究

冯祥亚

（重庆大学 统计与精算科学系，重庆 400030）

人民币汇率与地产行业间的联动关系研究

冯祥亚

（重庆大学 统计与精算科学系，重庆 400030）

随着我国房地产投资的国际化，汇率作为影响货币国际购买力的重要因素，它与地产行业的关系越来越密切。文章以上证地产指数做为地产行业发展状况的衡量指标，借助协整回归、误差修正模型、Granger因果关系检验等参数模型深入研究了人民币兑美元汇率与我国地产行业间的联动关系。结果表明，人民币兑美元汇率与上证地产指数间存在单向因果关系，汇率对地产指数的长短期走势都有显著性影响；建立了地产指数与汇率间的局部多项式回归模型，发现汇率对地产指数的影响程度因阶段而异。

协整回归；误差修正模型；Granger因果检验；非参数模型；局部多项式回归

0 引言

汇率是本国货币同外国货币进行兑换的比率，决定着国家货币在国际市场上的购买力。它不仅直接影响一个国家的对外贸易，还对国际资本流动产生重大影响，其均衡与否在很大程度上影响着国家经济的内外协调、稳定发展。在经济、金融全球化的今天，汇率正扮演着重要的角色，在国家的对外商品贸易及金融贸易中起着举足轻重的作用。

近年来，美国一直对人民币汇率施加升值压力，希望借此消减其强大的国际贸易逆差。就在今年3月15日，美国130名国会议员联名向白宫施压，要求奥巴马政府就人民币汇率问题采取强硬行动，迫使人民币升值的“政治战”硝烟味越来越浓。人民币汇率到底该走向何方，国家应该采取什么样的外汇政策，无疑是压在中国宏观经济上的一把利剑。本文借助参数及非参数模型来研究汇率与上证地产指数之间的联动关系，揭示上证地产指数跑赢大盘指数的原因，并为防范汇率风险，引导国际资本有效配置，制定科学、惠国、惠民的外汇管理制度提供决策依据。

1 数据指标的选取

2005年7月21日人民币汇率制度正式实行，本文选取2005年7月25日至2009年7月31日度数据做为研究样本。其中，汇率采用国家外汇管理局每天公布的直接标价法下人民币对美元的名义汇率，即1美元所能兑换的人民币数量。股市数据采用上证地产行业指数的每天收盘价。汇率数据来自国家外汇管理局网站(www.safe.gov.cn)，股市数据来自大智慧数据库。为了将汇率数据与股票数据相匹配，删除了一些汇市开盘而股市休市的汇率数据，最终获得了980个研究样本。为了消除可能出现的自相关及异方差对后期分析造成的影响，我们对所有样本数据进行对数变换处理，分别用REI、USD代表上证地产指数、人民币兑美元汇率，对数变换后的数据分别记为LREI=In(REI)，LUSD=In(USD)。

本文综合运用Johanson协整回归、误差修正模型(ECM)、Granger因果检验来研究人民币兑美元汇率与上证地产指数间的联动关系，最后建立了人民币兑美元汇率与上证地产指数间的非参数回归模型。

2 计量模型设计与实证

2.1 单位根检验

为了避免伪回归等问题的出现，在检验变量之间的协整关系之前需要验证序列是否平稳。本文利用增广的DF检验(Augmented Dickey-Fuller test)来验证序列是否平稳，结果如表1。

从表1可以看出，原始序列的ADF统计量都大于5%临界值，都是非平稳序列；一阶差分后的ADF统计量均小于临界值，是平稳的，因此原始序列都是I(1)，即一阶单整过程。

2.2 协整检验和误差修正模型的建立

如果几组时间序列都是不平稳的，但其差分形式都是平稳的，且具有相同的单整阶数，那么这些变量的某些线性组合有可能是平稳的。协整检验的目的就是决定一组非平稳序列的线性组合是否具有稳定的长期均衡关系。协整检验从检验对象上可以分为两种：一种是基于回归系数的协整检验；另一种是基于回归残差的协整检验。本文利用 “Engle-Granger两步法”[1]来研究上证地产指数与人民币兑美元汇率之间的长期均衡关系，这种检验方法是Engle和Granger在1987年提出的，是基于回归方程残差的协整检验。

设{yt}和{xt}均为 I(1)变量，首先利用最小二乘法(OLS)建立模型，进行协整回归：

其次对协整方程中的残差u赞t做平稳性检验，若残差序列是平稳的，则{yt}和{xt}存在协整关系，即存在长期均衡关系，否则就不存在长期均衡关系。在存在协整关系的条件下，引入误差项，建立如下的误差修正模型(ECM):

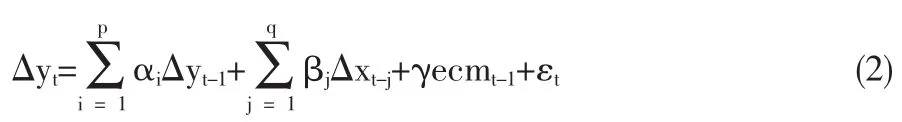
其中，ecmt为误差修正项，即协整方程中的残差项u赞t。 在误差修正模型中，各个差分项反映了变量短期波动的影响，γ被称为调整系数，反映了在t-1期yt-1关于β0+β1xt-1之间的偏差的调整速度，即反映了对偏离长期均衡的调整力度。因此，在误差修正模型中，被解释变量的波动可以分为两部分：一部分是短期波动；一部分是长期均衡。

由表1的ADF检验结果可以知道，LREI和LUSD均为一阶单整序列，可以利用“Engle-Granger两步法”来检验两者之间的协整关系。

第一步：以上证地产指数为被解释变量，以人民币兑美元汇率为解释变量进行协整回归，得到协整方程如下：

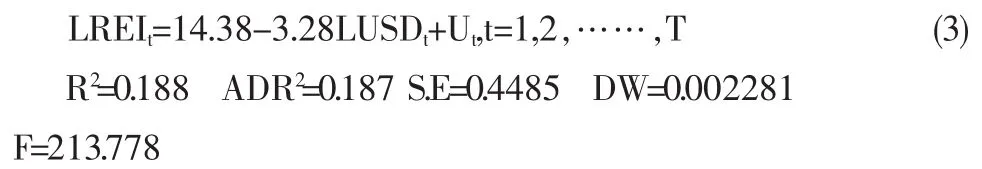
(3)式中系数都通过了显著性检验，但DW=0.002281，可能存在自相关现象，并且协整方程对应的R2=0.188，包含的原始数据的信息量太少。为此，在协整方程中加入解释变量和被解释变量的滞后项[2]，建立如下模型：

(4)式对应的各统计量都有显著改善，但此时LUSDt及其一阶滞后项LUSDt-1的系数都没有通过显著性检验，因此将一阶滞后项LUSDt-1去掉，重新建立方程如下：

利用上式求出LREI与LUSD之间的长期均衡关系：

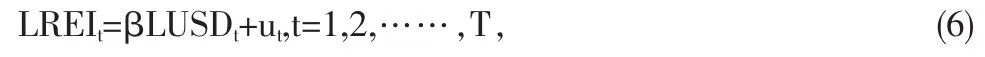
其中 β=-0.01005/(1-0.9975)=-4.065，因此，得到 LREI与LUSD之间的长期均衡关系为：

长期来看，人民币兑美元汇率与上证地产指数呈负相关关系，即人民币升值会引起地产指数的正向变动。现在对(4)式的残差序列u赞t做ADF检验，得到 ADF=-6.283，而 5%的临界值为-1.9474，ADF值远小于临界值，所以残差序列u赞t是平稳的，即ut∽I(0)，因此，LREI与LUSD之间存在协整关系。记(4)式的残差项u赞t为ecmt，并将其作为非均衡误差项进入误差修正模型，建立如下误差修正模型：

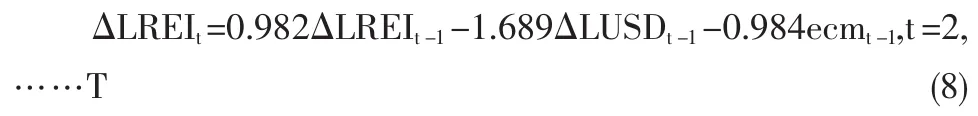
在误差修正模型中，各变量的回归系数都通过了显著性检验。因此，无论从短期来看，还是从长期来看，人民币兑美元汇率波动都是上证地产指数波动的原因。误差修正项ecmt-1的系数为-0.984，调整方向符合误差项反向修正原理，显示在一次冲击之后，短期值将向均衡值回复，并且这种调整力度比较大，能够保证地产指数与人民币兑美元汇率之间的长期协整关系。从模型看，上个观测期内地产指数变动一个单位，本期指数将正向变动0.982个单位；当期人民币汇率的变动并未对地产指数产生显著性影响，而上一观测期内汇率增量变动一个单位，本期地产指数将反向变动1.689个单位，即地产指数与人民币兑美元汇率呈负相关关系，人民币升值，将引起地产指数的正向变动。

2.3 Granger因果关系检验

前面我们利用协整检验及ECM误差修正模型验证了上证地产指数与人民币兑美元汇率之间存在长期均衡及短期波动关系，但并未说明它们之间的信息传导方向。下面我们利用Granger因果关系进行检验。Granger因果关系检验的基本思想是[1]：如果关于所有的 s＞0，基于(yt,yt-1,…)预测 yt+s得到的均方误差，与基于(yt,yt-1,…)和(xt,xt-1,…)两者得到的 yt+s的均方误差相同，则y不是由Granger引起的，否则，x就是y的Granger原因。利Eviews6.0进行Granger因果关系检验，得到结果如表2。

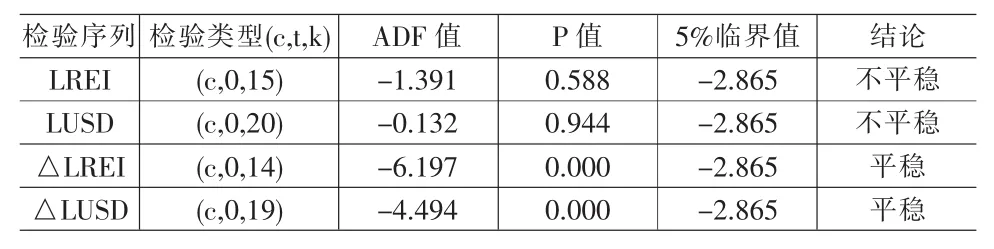
表1 序列的平稳性检验

表2给出了Granger因果关系检验的结果，在滞后期[3]分别取1、2、3的情况下，人民币兑美元汇率波动都是上证地产指数波动的Granger原因，但并不存在从地产指数到汇率的Granger因果关系，因此这正好说明了汇率的变动会引起国际游资的投资取向，从而影响地产行业的资金流动，进而影响地产指数的波动。

3 非参数拟合[4]

前面都是利用线性模型来研究地产指数与汇率之间的关系，这种模型的研究前提是变量之间必须满足线性关系及某些很明确的假设条件，并且回归函数的形式都是预先设定好的，只是函数中的参数未知，需要估计，统计学上称之为参数模型。参数模型的优点就是回归结果可以外延，且在小样本情况下可以对模型做进一步的统计检验、预测，并且模型参数都具有很明确的经济意义。但其缺点也很明显，如果模型的前提假设不成立或者函数形式出现设定错误，那么推断和预测都会出现偏差，甚至失去意义。因此，参数模型缺乏稳健性。为了解决参数模型中模型设定错误而出现的偏差，早在1964年Nadrarya[5]和Watson[6]就把非参数核估计引入到了回归模型的估计中。后来，Fan(1992[7],1993[8])、Fan和Gijbels(1992[9])发现局部多项式拟合不必进行边界修正，具有比非参数核估计更好的性质。

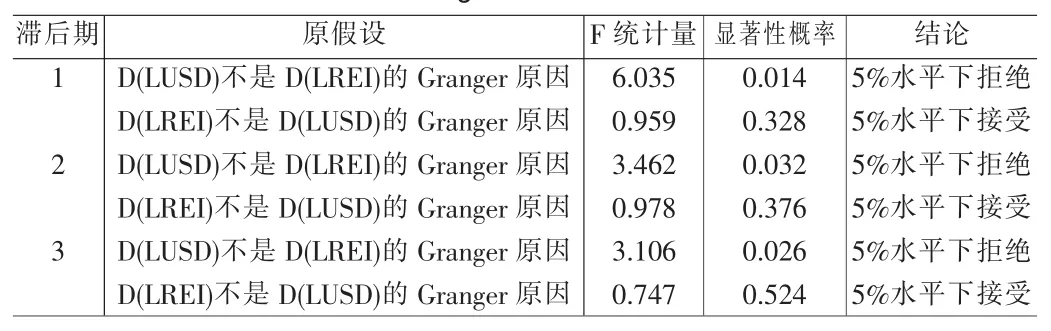
表2 Granger因果关系检验

假设变量X是影响变量Y的一个重要经济变量，它们之间的函数关系为：Y=F(X)，函数形式未知。可以建立以下的非参数模型：

其中ε为随机误差项，反映了影响Y的其他因素的综合效应。

假设有观测样本(Xi,Yi)，i=1,…,n,模型可以改写为：

这样，只需对每一个Xi估计出f赞(Xi)就可以了。若假定 f(X)在X=x0处存在p+1阶导数，则可以用x0(x0可取Xi,i=1,…,n)处的多项式来逼近函数值，即：

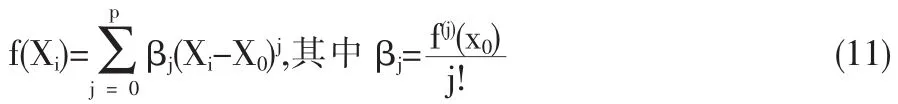
其中的参数βj=f(j)(x0)/j!就可以利用加权最小二乘法进行局部拟合，即最小化：

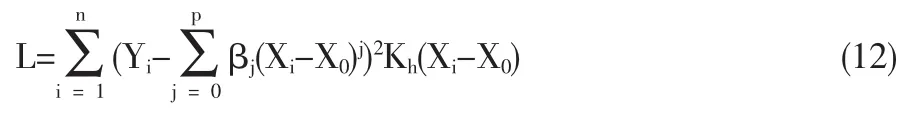
模型的估计效果与光滑参数h及权函数K(誗)的选取有关。其中光滑参数的选取原则是：使得估计的均方误差达到最小，实际中如果光滑参数太小，估计结果容易受随机因素的影响，会使估计曲线呈现不规则形状，而如果光环参数过大，估计曲线则过度平滑，数据波动的细微特征不易显现。本文中采用1977年Stone[10]提出的交叉核实法CV来确定平滑参数。其基本思想是：对每个观测点x=Xτ，首先在样本中剔除s 个观测点{Xt-τ≥s，Yt-τ≥s}然后将剩下的 T-s个观测点在 x=Xτ处进行局部回归，交叉核实函数定义为：

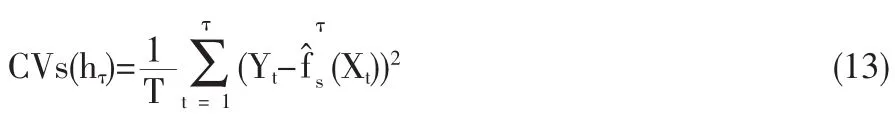
选择使CVs(hτ)达到最小时的平滑参数hτ。

在局部多项式估计中还要确定权函数k(誗)，确定权函数的原则[11]是：当观测点Xt与Xt0距离近时，所赋予的权重大，距离远时，赋予权重小。为避免边界点处对估计的影响，考虑在内点选择使均方误差达到最小的最优核函数Epanechnikov核函数

在左边界点-1，使用核函数K(z)=(1-z)I[0,1](z)；在右边界点使用核函数K(z)=(1+z)I[-1,0](z)。

本部分的所有计算都利用R[12]统计软件编写程序来实现。首先我们得到人民币兑美元汇率与地产指数之间的散点图如图1。

图1显示，人民币汇率与地产指数之间的关系很复杂，并非简单的线性关系。下面我们利用非参数局部多项式回归来拟合汇率与地产指数之间的关系，得到拟合图如图2。

从图2看，人民币兑美元汇率对上证地产指数的影响在不同的阶段影响程度是不一样的。2005年汇改之后，人民币兑美元汇率浮动加大，并逐步升值，此时上证地产指数也是一路走高（明显强势于上证综合指数），两者呈现明显的负相关关系，即人民币升值伴随着上证地产指数的逐步走强；但在2007年下半年，虽然人民币仍处于升值状态，但由于全球金融危机的爆发，地产指数也在金融风暴中进行了深度调整，但从图1可以看出，调整幅度明显小于上证综合指数，人民币升值是地产指数跑赢综合指数的重要原因。

另外，2008年7月份以来，人民币兑美元汇率一直在6.82元左右小幅浮动，对地产指数的信息贡献较少，解释能力较弱；实际上，这个时间段内地产指数的走向更多的是受经济形势及国家宏观经济政策的影响。

图3显示，局部多项式对前期拟合效果很好，但对2008年7月份以来的地产指数走向拟合效果不甚理想，主要由于在这段时间内人民币兑美元汇率弹性较小，一直徘徊于6.82元附近，对地产指数走势的解释能力较弱。

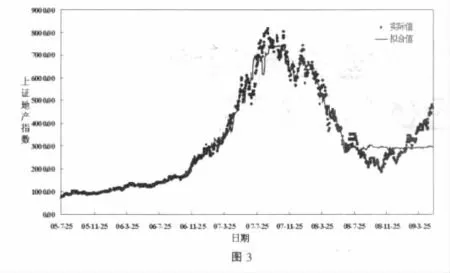
4 结论

随着经济全球化及人民币汇率制度的不断完善，人民币汇率波动将更加富有弹性，汇率必然会对资本价格产生更深远的影响。因此，研究汇率与资产价格之间的联动关系，对保持资本价格的稳定，避免过渡波动有很重要的现实意义。2005年以来，我国房地产市场投资热度锐增，导致房价居高不下，增强了经济学家对我国房市“泡沫”的预期[13]。本文通过研究2005年7月25日到2009年5月18日期间，上证地产指数与人民币兑美元汇率之家的联动关系，得到了以下结论：

（1）协整检验表明人民币兑美元汇率与上证地产指数之间存在长期稳定的均衡关系，人民币兑美元汇率与上证地产指数间呈现显著地负相关关系，即人民币升值伴随着地产指数的同向变动。

（2）从误差修正模型看，人民币兑美元汇率的短期波动也是上证地产指数产生波动的原因之一。

（3）Granger因果关系检验表明汇率与地产指数间存在单向因果关系，即人民币兑美元汇率波动是指数波动的Granger原因，但地产指数对汇率的短期影响并不显著。

（4）非参数模型拟合结果表明人民币兑美元汇率对上证地产指数在不同阶段的影响程度是不一样的，2008年7月之后汇率弹性变小，此时汇率对地产指数的解释能力则相对较弱，但随着国家外汇政策的完善，汇率市场化程度的加深，汇率对地产指数的解释能力将会逐步回归均衡状态。

[1]高铁梅.计量经济分析方法与建模:Eviews应用及实例[M].清华大学出版社,2006.

[2]韦邦荣,杨玉生.中国财政支出与GDP之间的关系的协整分析与误差修正模型研究[J].2006，（14）.

[3]李天德,张爽.金融发展与经济增长的协整分析[J].西南民族大学学报，2009，（10）.

[4]叶阿忠.我国通货膨胀的非参数回归模型[J].数理统计与管理,2002,21(1).

[5]Nadaraya,E.A.On Estimating Regression[J].Theory of Probability and Its Applications,1964,（9）.

[6]Watson,G.S.Smooth Regression Analysis[J].Sankhya,Series A,1964,（26）.

[7]Fan,J.Design Adaptive Nonparametric Regression[J].JASA,1992,（87）.

[8]Fan,J.Local Linear Regression Smoothers and Their Minimax Efficiences[J].Annals of Statistics,1993,（21）.

[9]Fan,J.,I.Gijbels.Variable Bandwidth and Local Linear Regression Smoothers[J].Annals of Statistics,1992,（20）.

[10]Stone C J.Consistent Nonparametric Regression[J].Ann.Statist,1977，（5）.

[11]李竹渝,鲁万波.经济、金融计量学中的非参数估计技术[M].科学出版社，2007.

[12]薛毅,陈立萍.统计建模与R软件[M].清华大学出版社,2007.

[13]陈婕,路静,高鹏,董纪昌.人民币汇率波动与我国房价关系的实证研究[J].数学的实践与认识，2009,39(13).

[14]施佳欢.房地产板块指数的双因子模型分析[J].市场周刊，2009,（9）.

C812

A

1002-6487(2011)04-0082-04

冯祥亚（1987-），男，河南泌阳人，硕士研究生，研究方向：金融数据建模、金融数据挖掘。

（责任编辑/浩 天）