基于实物期权的专利资产证券化中的单一专利价值评估

靳晓东

（北京工业大学 知识产权研究中心，北京 100124）

基于实物期权的专利资产证券化中的单一专利价值评估

靳晓东

（北京工业大学 知识产权研究中心，北京 100124）

专利资产证券化作为一种新型融资方式已为发达国家所采用，对于推动金融创新与科技发展起到了重要的作用。我国也开始了该项交易的试点。由于被证券化专利的特点，导致传统评估方法在对其进行评估时具有局限性。文章使用实物期权法对专利资产证券化中的单一专利的价值进行了评估，并建议使用模糊综合评价法对本模型的评估结果进行修正，以获得更为接近真实值的评估值。

专利资产证券化；实物期权；价值评估

0 引言

专利资产证券化作为一种新型融资方式已为发达国家所采用，对于推动金融创新与科技发展起到了重要的作用。为落实我国国家知识产权战略纲要的精神、加快知识产权事业的发展，我国也开始了该项交易的试点工作。在专利资产证券化的过程中，对被证券化专利价值的准确评估是完成该项交易的核心。作为一种无形资产，被证券化专利具有预期收益不确定、决策灵活、技术不可替代等特点，导致对这类专利评估的难度较大。传统的评估方法（成本法、市场法、收益法）在对其评估时具有局限性，从而给该项交易的顺利进行带来了困难。

从实物期权的角度来看，专利权赋予决策者在其法定有效期内的任意时刻选择立刻实施、等待实施或是不实施被证券化专利的独占性权利，因此被证券化专利可以视为一项美式期权，其评估计算期则可以划分为等待阶段和实施阶段。在等待阶段，决策者不实施专利，而是决定延迟投资以等待更好的实施时机；当决策者决定实施专利后，即刻进入实施阶段，决策者通过一定的初始投资使专利技术获得实施，并通过项目运营而获取一定的收益。所以，可以采用实物期权法对其进行评估。

在专利资产证券化的过程中，专利资产池的构成分为单一专利与专利组合两种模式，对这两种不同的模式采用的评估模型有所不同，本文主要探讨对被证券化单一专利的价值评估。从决策时间是否连续的角度来看，实物期权定价模型可分为连续时间模型和离散时间模型两类。本文选择连续时间模型，主要是因为在对被证券化单一专利价值评估的时候，被证券化单一专利的实施决策具有较强的灵活性，可以在该专利有效期的任意时刻实施，因此被证券化单一专利的决策时间可以看作是连续的。

1 基本假设

本文的模型及分析建立在如下假设之上：

第一，被证券化专利处于一个完全、有效的市场中。完全、有效的市场也可以看作一个无摩擦的市场，即：（1）在该市场中不存在交易成本及差别性税收；（2）市场允许卖空，譬如没有对于保证金或者垫头的要求；（3）市场中的资产可以完全分割，即资产的所有份额都是无限可分的；（4）市场中不存在套利机会，借款和贷款有着相同的利率且不受限制[1]。完全、有效的市场假设是为了确保该市场中交易的连续性。

第二，市场的无风险利率是已知的，且在被证券化专利的计算期内不发生变化。无风险利率记为r。

第三，被证券化专利视为已经得到批准。

第四，为实施被证券化专利所进行的初始投资不可逆的，这主要是因为在本文所研究的范围之内，由于被证券化专利在技术上具有独特性，因此为实施该专利所进行的投资只能用于该专利的实施及相关产品的生产，而不适用于其他产品的生产过程[2]。这部分投资可以看作沉没成本，因此收益法不适用于被证券化专利价值评估[3]。

第五，决策者对被证券化专利拥有完全的决策权，因此被证券化专利赋予决策者的权利可以看作实物期权。

第六，不存在代理冲突的问题[4]，因此参与专利资产证券化过程的各方均以专利资产价值最大化为目标。

第七，被证券化专利所对应的实物期权有分红，红利记为δ。对被证券化专利而言，红利可以看作实施专利的机会成本。

第八，实施被证券化专利所获得的现金流入不能再用于投资。

第九，在专利资产证券化的过程中不存在跳跃因素，即不会出现使被证券化专利预期收益发生显著的突然变化的非预期因素。

第十，被证券化专利在证券化的过程中不存在由投资决策变化而引起的调整成本[5]。

2 专利资产证券化中的专利价值评估模型

2.1 主要变量设定

（1）被证券化专利价值评估的计算期

被证券化专利价值评估的计算期为拟进行证券化的期限，起点时刻记为0，终点时刻记为T，计算期为[0，T]。计算期应在被证券化专利的法定有效期之内。在实践中，专利资产证券化的期限一般为5～10年。

（2）实施被证券化专利所需的初始投资

实施被证券化专利所需的初始投资记为X。在实践中，被证券化专利都是经过发起人反复调研、反复筛选而选中的具有相对优良的获利能力的专利，与一般专利相比，实施这类专利的初始投资往往是在决策阶段能够确定的；否则，发起人所面临的投资风险将大大增加。所以，在本模型的计算期内，可以假定初始投资X为一个已知常数。对应于美式看涨期权，初始投资X相当于期权的执行价格。

（3）被证券化专利实施后的预期净收益

被证券化专利实施后的预期净收益包括：专利实施后因该专利而产生的销售收入等各项收入以及预期将会产生的销售费用、经营费用、管理费用、运营维护费用等各项费用互相抵消之后的净值，这一净值受到很多不确定性的影响，可以看作随机变量。被证券化专利实施后的预期净收益记为S，服从如下的几何布朗运动[6]：

其中，(α-δ)dt描述了S的收益率随时间变化的特征。α是专利实施后的预期收益率。δ是实施被证券化专利的机会成本，相当于金融期权中的股票分红。σdz描述了S的不确定性特征。σ是被证券化专利实施的预期收益率的标准差，描述S的波动程度；dz是维纳过程增量，且有dz=ε，εN(0，1)。由于被证券化专利视为已经取得，故S的不确定性程度仅取决于决策者对未来的预见性[5]。

对应于美式看涨期权，S相当于期权的标的资产价格（如股票价格）。McDonald和Siegel指出，假设服从几何布朗运动是合理的。可以看作执行专利后可获得的市场价值，如果实施专利，假设实施专利的公司仅拥有这一项资产，那么S就是该公司股票的价格，也就是说，S可以看作一项金融资产。在金融领域，股票价格服从几何布朗运动是常用的基本假设。因此假设S服从几何布朗运动是合理的[7]。

综上，被证券化专利价值是在计算期[0，T]上预期净收益S 和时间 t的函数，记为 F(S，t)。

2.2 求解目标

前面指出，被证券化专利可以看作美式看涨期权。与欧式期权相比，美式期权最大的特点在于其执行时间可以自由选择。这一特点在期权定价方法中体现为美式期权必须要考虑自由边界问题，具体到本模型是[8]：

被证券化专利存在一个最优实施边界Γ：{S=S(t)，0≤t≤T}。这一边界把区域Ω={0≤S≤∞，0≤t≤T}划分为以下两个部分：

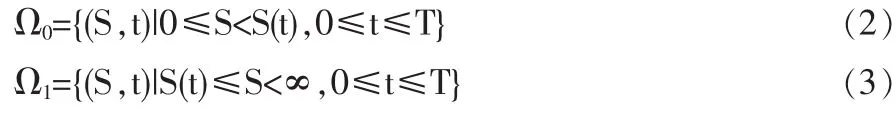
且：

其中，S(t)为被证券化专利的最优实施边界。

第一个部分Ω0是没有到达最优实施边界Γ的区域，在这一区域内决策者会选择延迟投资以等待实施被证券化专利的最佳时机，本文称之为等待区域。在等待区域Ω0有：

第二个部分Ω1是达到最优实施边界Γ之后的区域，在这一区域内决策者会选择实施被证券化专利以获得收益，本文称之为执行区域。在执行区域Ω1有：

且在整个计算期[0，T]，都有：

本模型的目标就是评估被证券化专利价值F(S(t)，t)。

2.3 目标函数

要想实现本模型的目标，就必须首先确定F(S，t)在所满足的随机微分方程。根据伊藤引理可以得到被证券化专利价值满足如下方程：

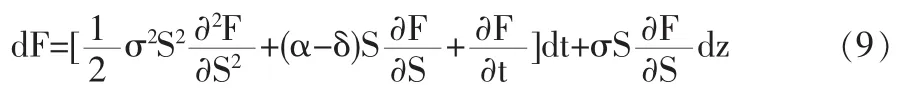
基于无套利理论的对冲原理指出，对于给定的期权F，在相反方向交易△份额的标的资产S，可以使得由此所构成的投资组合Π=F-△S是无风险的。

根据对冲原理，在本问题中可以构建这样一个投资组合Π：

买入一份F的同时卖出△份S

假定在t时刻形成该投资组合Π，且在时段[t，t+dt]上不改变所持有的各资产的份额。由于Π是无风险的，所以在t+dt时刻该投资组合Π的收益率为无风险利率，用公式可以表达为：

因为考虑到支付股息δ，所以有：

所以在t+dt时刻该投资组合Π的收益为：

将式（9）代入式（12）可以得到：

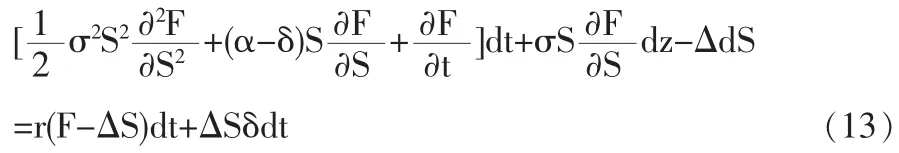
将式（1）代入式（13）：

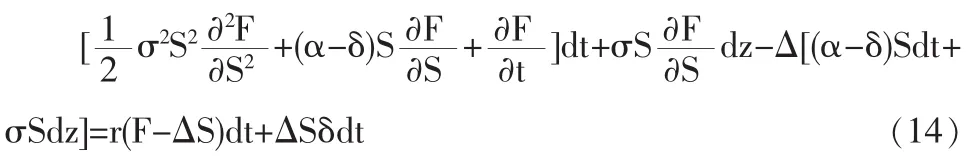
整理后可以得到：

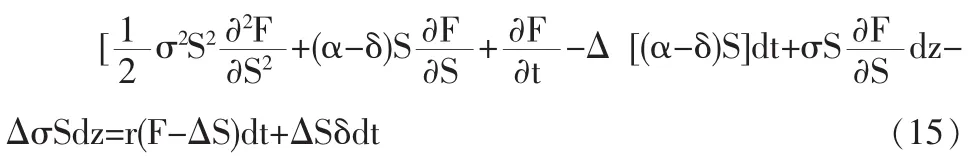
因为式（15）的右端是无风险资产组合，所以其左端的随机项为0，即：

解得：

将式（17）代入式（15）得：

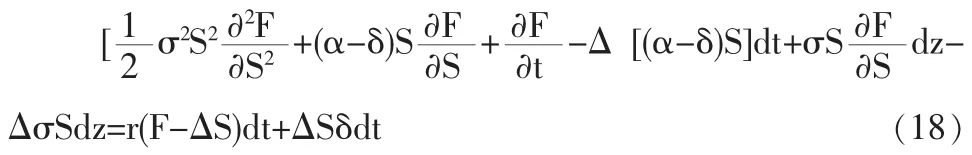
因此，应用无风险对冲原理及伊藤引理可以得到，当(S，t)∈Ω1时被证券化专利价值满足的随机微分方程如下：

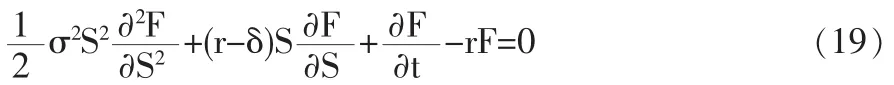
2.4 边界条件

在求出被证券化专利价值所满足的随机微分方程之后，还需要三个边界条件才能实现求解。在本模型中，完整的边界条件应由最优实施边界上的自由边界条件及两个端点处的初值条件和边值条件构成：

（1）自由边界条件

本模型的自由边界条件为，在最优实施边界Γ：{S=S(t)，0≤t≤T}上：

其中，式（20）和式（21）保证了被证券化专利价格的连续性。它体现了美式期权的定价原则，即期权持有人执行最优实施策略以使期权价值实现最大化。当到达最优实施边界时，才会决定实施该专利。

（2）边值条件

在t=T时刻，专利权即将到期，此时被证券化专利所对应的实物期权的内在价值等于到期日价值，即：

（3）初值条件

当专利实施后的预期收益为0时，被证券化专利不会实施，因此其价值为零，即当S=0时，必然有：

2.5 模型求解

根据隐式差分法的原理，将被证券化专利实施后的预期净收益等分为M段，每一段为△S=Smax/M，其中Smax是S的最大值，其取值可以通过经验预测。将计算期[0，T]等分为N个时间跨度相等的子区间，每个子区间的长度均为△t=T/N。根据上述划分，可以进行以下近似：

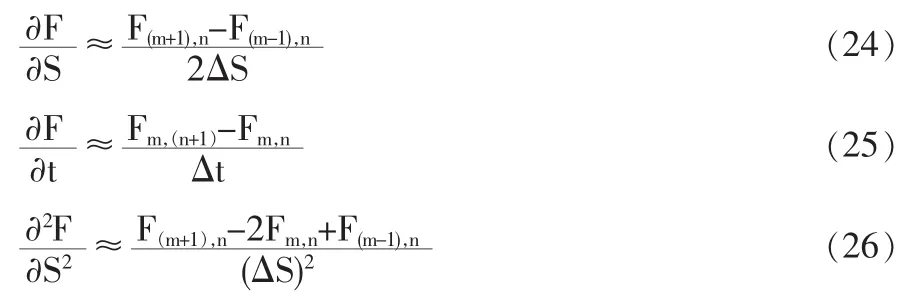
将式（24）至式（26）代入式（19）：

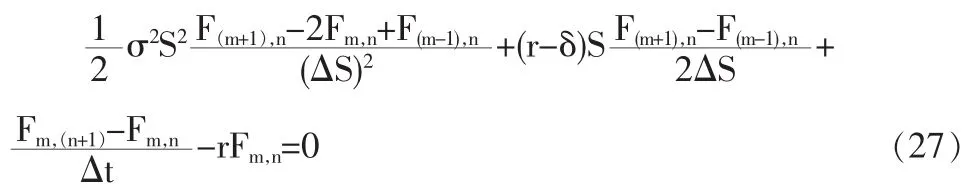
将△S=Smax/M代入式（27），经整理、化简可以得到：

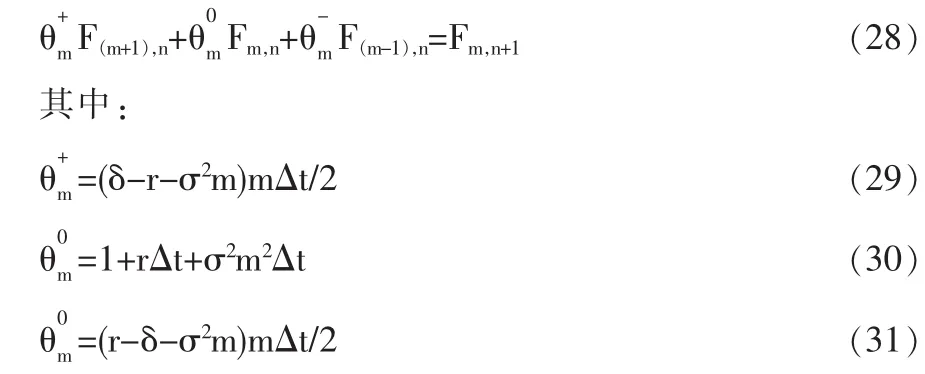
假设时刻标的资产价值m△S可以获得，则被证券化专利在t=T时刻的现值为：

根据式（32）可以分别计算得到 F1，T，F2，T，…，F（M-1），T的值（共 M-1个）。

利用式（28）可以得到在T-△t层由M-1个方程组成的线性方程组：

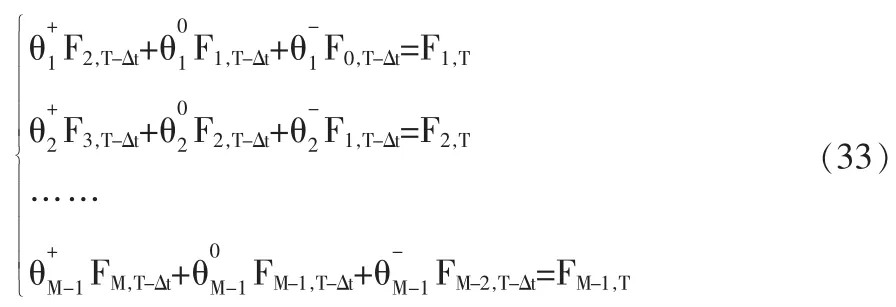
其中，F1，T，F2，T，…，F（M-1），T均已根据式（32）求出。

另外，根据边界条件可以得到，在T-△t层存在如下等式关系：

式（33）～（35）联合求解，可以得到在 T-△t层，F1，（T-△t），F2，（T-△t），…，F（M-1），（T-△t）的取值（共 M-1 个）。

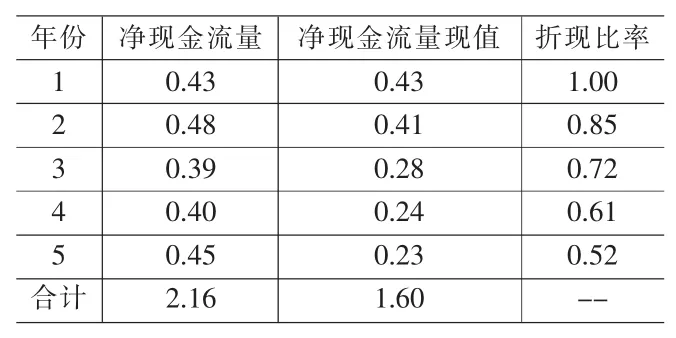
将 F1，（T-△t），F2，（T-△t），…，F（M-1），（T-△t）分 别与 △S，2△S，…，（M-1）△S 比较。 如果 Fm，（T-△t）

继而重复上面的过程，逐步倒推直至获得 F1，0，F2，0，…，F（M-1），0的取值（共 M-1 个），在这 M-1 个值中取最大值，即为本模型要求的数值解。

2.6 变量及参数分析

在本模型中，影响评估结果的重要变量为：被证券化专利实施后的预期收益S；实施被证券化专利的初始投资X；被证券化专利的评估期上限T。影响评估结果的重要参数为：无风险利率r；实施被证券化专利的机会成本δ；实施被证券化专利的预期收益的波动率σ；实施专利的预期收益的收益率α。下面展开对这些变量和参数的分析，讨论它们在实践中如何选取。

第一，被证券化专利实施后的预期收益S。根据隐式差分法的原理，只要给出实施被证券化专利所能获得的预期总收益的最大值，在实践中可以使用商业计划书中的预估值。

第二，实施被证券化专利的初始投资X。初始投资X在本模型中被假定为已知，可以从专利证券化的商业计划书中获得这一数据。在实践中，初始投资主要用于厂房、设备等，所以基本上都可以在实施专利之前确定；而且发起人也往往会在筛选的过程中排除初始投资不确定的专利。

第三，被证券化专利的评估期T。在本模型中，由于不存在跳跃因素，所以T可看作是已知的，等于该项专利被证券化的期限。

第四，无风险利率r。从国外的相关文献上来看，无风险利率一般可以选取国库券利率。但是在我国的实践中，更常见的是选择银行存款利率。

第五，实施被证券化专利的机会成本δ。这一机会成本也可以看作被证券化专利所对应的美式看涨期权的分红，等于实施该专利的投资的银行存款利率。

第六，实施被证券化专利的预期收益的波动率σ。可以根据商业计划书给出的预期收益进行估算。但需要注意的是，波动率受到发起人风险承受能力的影响，其取值具有较强的主观性，预期收益表示为不同数量级时，波动率的大小也不同。因此，波动率σ的选取需要考虑发起人的经济实力及抗风险能力。

第七，实施专利的预期收益的收益率α。根据无套利原理和风险中性假设，收益率在推导的过程中可以直接消去，因此对结果不产生影响。但在实践中，需要选择折现率将预期净收益折现至计算期的起点。一般的做法是选择投资者的最低预期收益率。

3 算例分析

在上述假设条件下，下面对一项医药专利进行证券化。证券化的期限为5年，初始投资为1亿元人民币。无风险利率和机会成本均选取中国人民银行2008年12月13日发布的金融机构人民币存款基准利率（5年及以上），r＝3.60%，δ＝3.60%。预期收益为1.60亿元人民币 （折现率选取最低预期收益率18%，由公司决策者参照行业基准折现率给定），预期收益净现金流量详如表1所示。

表1 某医药专利预期现金流量表(单位：亿元人民币)

根据表1的现金流量数据，可以计算得到预期收益的方差σ＝0.10。将被证券化专利实施后的预期净收益现值等分为1000 段（M＝1000），将计算期等分为 1000 段（N＝1000），使用Matlab软件编程求解。

根据计算机运行结果，该项医药专利的价值为496万元人民币。

4 结论

本文在一系列假定下给出了专利资产证券化中的专利价值评估模型。但是，由于该项交易刚刚起步，所以，还需要在实践的基础上不断对评估模型进行完善，并在后续的研究中逐步放宽假设条件，将评估模型推广至更一般的情况。此外，从本文的分析中还可以发现，在使用实物期权法对被证券化专利进行评估的时候，波动率的选取具有一定的主观性，所以还可以使用模糊综合评价法对本模型的评估结果进行修正，以获得更为接近真实值的评估值。

[1]J.C.Hull.Options,Futures and Other Derivatives （5thEdtion）[M].New Jersey：Prentice-Hall.Pearson Education.Upper Saddle River，2003.

[2]R.S.Pindyck.Irreversible Investment,Capacity Choice,and the Value of the Firm[J].American Economic Review，1988,78(5).

[3]R.S.Pindyck.Irreversibility,Uncertainty,and Investment[J].Journal of Economic Literature，1991,XXIX.

[4]R.Brosch.Portfolios of Real Options[M].Berlin:Springer Berlin Heidelberg，2008.

[5]S.Majd,R.S.Pindyck.Time to Build,Option Value,and Investment Decisions[J].Journal of Financial Economics，1987,18(1).

[6]J.D.Paddock,D.Siegel,J.Smith.Option Valuation of Claims on Physical Assets:The Case of Offshore Petroleum Leases[J].Quarterly Journal of Economics，1988,103(3).

[7]R.McDonald,D.Siegel.The Value of Waiting to Invest[J].Quarterly Journal of Economics，1986,101(4).

[8]L.Jiang,C.Li.Mathematical Modeling and Methods of Option Pricing[M].Singapore:World Scientific Publishing Co.Pte.Ltd.2005.

F224

A

1002-6487（2011）04-0050-04

北京市中青年骨干教师培养计划资助项目（J201107200801）；北京工业大学知识产权研究基地资助项目（X3011017200801）；

北京工业大学高教研究资助项目（ER2009-B-52）；北京工业大学人才强教深化计划-教学技能项目（01100054R6001）

靳晓东（1971-），男，四川成都人，博士研究生，副教授，研究方向：知识产权管理、知识产权法。

（责任编辑/亦 民）