城镇居民最低生活保障线的测定

印凡成，刘丽莹，黄健元

（河海大学a.理学院；b.公共管理学院，南京 210098）

城镇居民最低生活保障线的测定

印凡成a，刘丽莹a，黄健元b

（河海大学a.理学院；b.公共管理学院，南京 210098）

文章选用扩展线性支出法作为城镇居民最低生活保障线的测定方法。讨论了最低生活保障线的预测模型，即先测定一个基准年的最低生活保障线，再根据物价指数的预测结果，测定其他年份的最低生活保障线，对模型中涉及的物价指数这一重要参数构建了组合预测方法；测定和预测了2002～2015年江苏省城镇居民最低生活保障线的理论值。

最低生活保障线；扩展线性支出模型；组合预测

随着市场经济的发展和经济体制改革的深入，我国的经济发展水平取得了长足的进步，但也随之带来了一些社会问题，如失业率上升、贫富差距扩大等等。尤其在城市中，失业职工增多和物价上涨使低收入家庭的生活陷入困境，城镇贫困现象严重。因此怎样建立合理高效的社会保障制度是亟需解决的问题。其中最低生活保障制度是社会保障体系中的“最后一道防线”，也是化解社会矛盾、维护社会稳定、促进社会公平、保证经济体制改革顺利进行的有力保障。因此,研究科学适用的城镇最低生活保障线的测定方法具有重要意义。

最低生活保障线的测定方法主要有：市场菜篮法、恩格尔系数法、国际贫困线法、马丁法、扩展线性支出法等。其中扩展线性支出法是一种数学模型方法，避免了确定生活必需品清单时个人主观因素的影响和难以确定的价格问题，在统计软件大规模应用的今天，这一方法变得十分简便易行。通过对各种方法的适用性分析，本文将选用扩展线性支出法作为测定城镇居民最低生活保障线的基本方法。

1 扩展线性支出系统模型

扩展线性支出系统（ELES）模型是路迟（Liuch）于1973年在线性支出系统模型的基础上进行改进的模型，它广泛应用于居民的消费结构分析。该模型把人们的消费支出分为两部分，一部分为基本消费支出，另一部分为超额消费支出。基本消费支出是维持基本生存需求的必须支出，它不会受收入水平的影响，而超额消费支出是在满足基本需求之后的额外支出。因此可以通过求解其基本消费支出得到最低生活保障线。

扩展线性支出系统模型为：

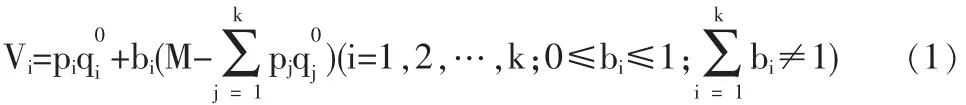
其中，Vi为第i种商品的消费支出；pi为第i种消费品的价格；为第i种消费品的基本需求量；bi为第i种消费品的边际消费倾向；M为可支配收入。

模型中，pi为居民对第i种商品的基本消费支出；bi(M-为居民对第i种商品的超额消费支出。虽然每个人对商品的需求不同，但是维持最低生活标准的基本需求是一致的。因此，维持居民最低生活所需的k种商品的基本费用之和，即为最低生活保障线：

由于（1）式可写为

其中，εi为随机扰动项。

参数ai与bi的值可以用最小二乘法估计出来，用其无偏估计值和表示。

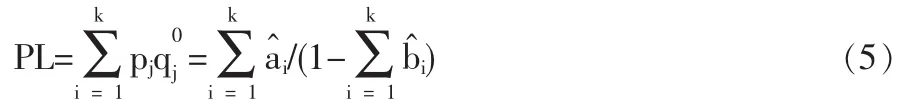
2 最低生活保障线的预测模型

考虑到居民的基本生活需求在较长时间内不会有大的变化，因此影响最低生活保障线的最主要因素是物价的影响。所以本文采用先测定出某一基准年的最低生活保障线，然后根据此后各年物价指数的变化来预测最低生活保障线的方法，即设基准年的最低生活保障线为PL0，目标年第n年的物价指数为Pn，则目标年的最低生活保障线为：

其中，Pn是目标年第n年相对于基准年的物价指数。

基准年的最低生活保障线PL0可根据前面所讨论的方法测定，这样最低生活保障线的预测问题，转化为各年物价指数的预测问题。

3 物价指数的组合预测模型

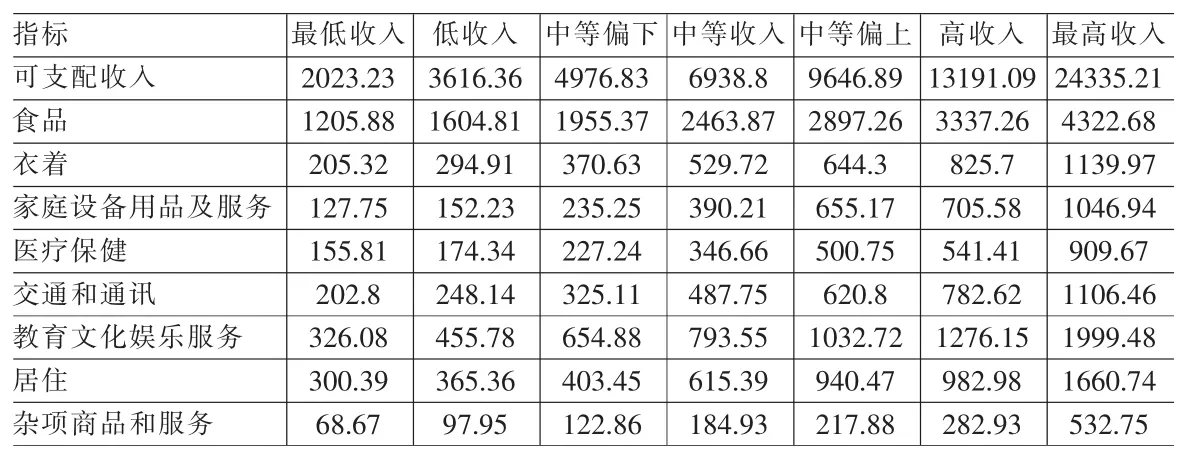
表1 2002年城镇居民家庭人均收入支出情况 （单位：元）

我们知道任何一种定量的预测方法都有缺陷，为了提高预测的精度和可靠性，结合本文中数据的特点，本文将采用灰色模型预测法和二次指数平滑预测法作为单项预测，构建组合预测方法，对物价指数Pn进行预测。

3.1 灰色预测法

设非负的原始数据序列为y(0)，经累加的数据序列为y(1)，则y(1)满足一阶微分方程：

其中，α为发展系数，μ为灰色作用量，可利用最小二乘法进行估计。

解上述微分方程得时间响应函数：

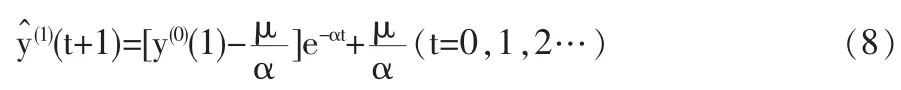
累减后得到原始数据序列的预测公式：

3.2 二次指数平滑预测法

设观测序列 yt（t=1，2，…T），α 为加权系数，0<α<1，一次指数平滑公式为：

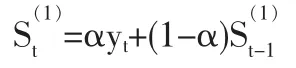
类似地，二次指数平滑公式为：

预测模型（Brown单系数线性平滑预测模型）

加权系数α的选择一般要遵循：如果序列的基本趋势比较平稳，则α的取值应取小一些；如果预测目标的基本趋势已发生系统性的变化，则α应取得大一些。本文将比较均方误差的大小，来选定合适的α。

3.3 组合预测

本文中组合预测的权重的确定参考文献[6]中的方法，分别计算两种单项预测方法的均方误差然后根据MSE确定两种方法的权重ω1和ω2，得到组合预测：

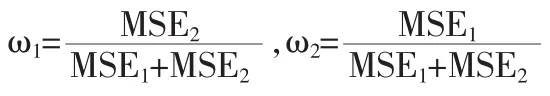
4 实证分析

根据统计年鉴的数据，城镇居民的消费支出被划分为8类，分别为食品、衣着、家庭设备及服务、医疗保健、交通与通讯、教育文化娱乐服务、居住、杂项商品与服务。同时根据人均收入情况把城镇居民分为最低收入、低收入、中等偏下、中等收入、中等偏上、高收入和最高收入七组。

本文选取2002年作为基准年 （这是因为根据2000～2008年的数据计算各年最低生活保障线时，只有2002年各项指标均拟合得很好，其他年份都有较多参数不能通过显著性检验）。具体数据如下：2002年城镇居民家庭人均收入支出情况见表1；2002～2008年城镇居民消费物价指数 （1978年＝100）见表 2。

表2 2002年～2008年城镇居民消费物价指数 （1978年＝100）

4.1 2002年江苏省城镇居民最低生活保障线的测定

首先分别对每一大类商品按不同的收入阶层进行一元线性回归，从而得到8个回归方程，计算出对应的参数（见表3）。

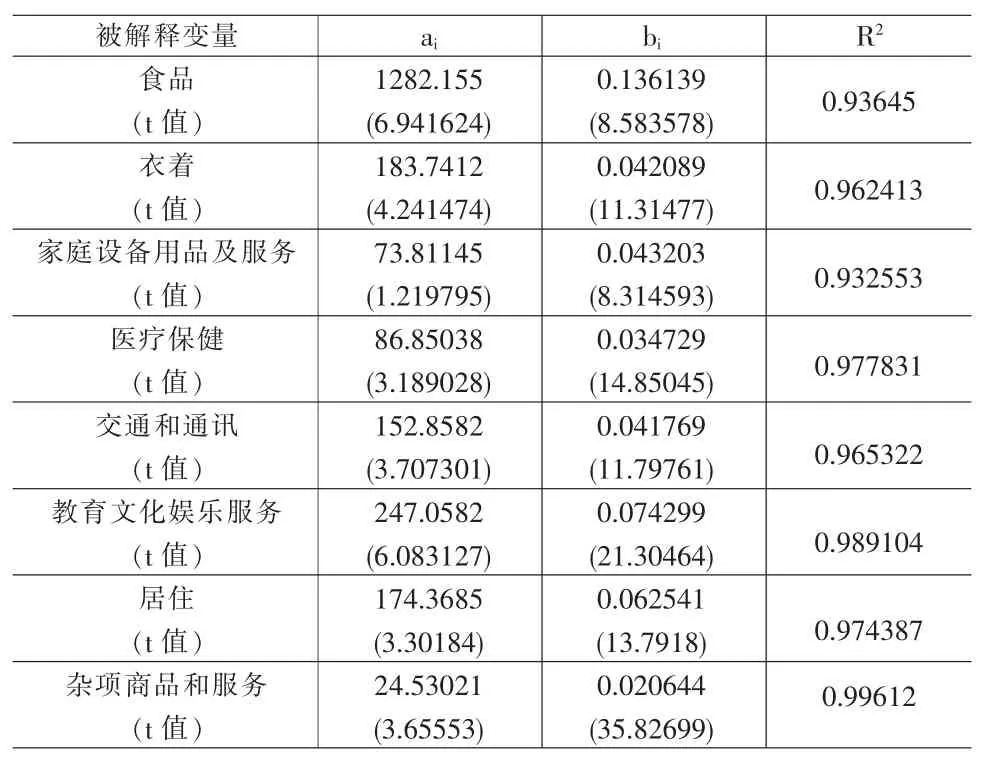
表3 回归方程参数及检验表

在5%的显著性水平下，若t>2.571，则说明以5%的显著性水平拒绝原假设，建立的回归方程有显著意义。从表中数据可以得出只有“家庭设备用品及服务”指标的ai不能通过显著性检验。这可能是由于样本点不够多造成方程拟合偏差，使此系数不显著，所以在求最低生活保障线时应该把此系数剔除。

建立扩展线性支出系统如下：

（1）食品：V1=1282.155+0.136139M (R2=0.93645)

（2）衣着：V2=183.7412+0.042089M (R2=0.962413)

（3）家庭设备用品及服务：V3=73.81145+0.043203M(R2=0.932553)

（4）医疗保健：V4=86.85038+0.034729M(R2=0.977831)

（5）交通和通讯：V5=152.8582+0.041769M(R2=0.965322)

（6）教育文化娱乐服务：V6=247.0582+0.041769M(R2=0.989104)

（7）居住：V7=174.3685+0.062541M(R2=0.974387)

（8）杂项商品和服务：V8=24.53021+0.020644M(R2=0.99612)

利用表4所提供的数据,可以计算江苏省最低生活保障线:

Σai=2151.56127，Σbi=0.41221005

OK=Σai/(1-Σbi)=3660.425415

上面得到的结果是年最低生活保障线，换算成月收入为305.04元。

4.2 2009～2015年江苏省城镇居民消费物价指数的预测

（1）原始序列

y0=(482.2，486.5，504.5，514.6，522.8，544.3， 572.6)。

（2）级比平滑检验

σ =(0.991161，0.964321，0.980373，0.984315，0.9604500，0.950576)

σ(k)=（0.950576，0.991161）奂（0.1353，7.389）

表明序列y0是平滑的，可作灰预测。

已知 n＝7；有界区：（ ， ）=（0.7789，1.1284）；级比区：σ（k）∈（0.950576，0.991161）奂（0.7789，1.1284），表明级比区在界区内，可以获得精度较高的GM(1,1)模型。

（4）GM(1,1)建模

用 Matlab软件编程计算出 α=-0.0306，μ=462.7196，从而得到白化型GM(1,1)为：

（5）检验

相对残差 e(0)=(0，1.629，4.553，0.893，8.722， 3.749，7.509)，平均残差e(0)(avg)=3.865，均方误差误差为：24.3856；方差C=0.011，误差概率P=1.0，模型精度为一级，因此可以用作预测模型。

（6）预测

由（13）式得到2009～2015年的预测结果，见表4。

对物价指数进行二次指数平滑预测，由以下步骤进行：

首先令α取不同的值进行试算，取均方误差最小者为加权系数。通过计算，当α＝0.4时，均方误差最小，为10.936。故此处选取α＝0.4。

根据（11）式，对2008年以前的数据进行逐年预测，并得到2008年以后数据的预测公式：

y赞T+m=563.6842+13.6564m（m=1，2…）

其中 m为时间，2009年取 1，2010年取 2，依次类推2015年取7，预测结果见表4。

表4 物价指数预测情况

4.3 组合预测

分别求出两种单项预测方法的均方误差MSE1＝24.3856，MSE2＝10.936，则

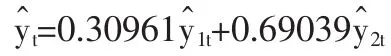
由此得出2002～2015年的组合预测值，见表4。

4.4 2003～2015年江苏省城镇居民最低生活保障线的预测

已知基准年2002年的最低生活保障线为305.04元。由于（6）式中Pn是相对基准年的物价指数，则首先把以上预测结果转化为相对基准年的物价指数，见表5。

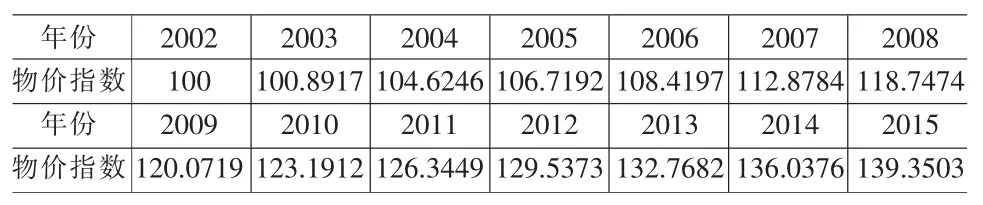
表5 相对基准年的物价指数 （2002年＝100）

根据（6）式，计算出2003～2015年江苏省城镇居民最低生活保障线，见表6。

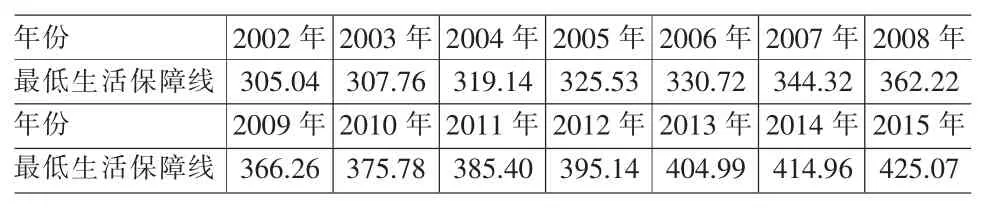
表6 2002～2015年江苏省城镇居民最低生活保障线

5 结论

（1）本文采用扩展性线性支出系统模型法对江苏省2002年城镇居民最低生活保障线进行了测定,然后将物价指数进行了灰色模型预测方法和二次指数平滑预测法的组合预测，进而预测出了2003～2015年江苏省城镇居民最低生活保障线的理论值。这是在最低生活保障线测定方法研究和应用上的一次有益尝试。

（2）根据预测结果，2002年江苏省城镇居民最低生活保障线为每月305.04元。此后随着物价的变动，最低生活保障标准将逐步增加。到2015年江苏省城镇居民最低生活保障线为每月425.07元。目前江苏省的月最低工资标准为一类地区960元、二类地区790元、三类地区670元。这里测算出的最低生活保障线与最低工资标准相比，还有着一定的距离，这将对贫困居民的就业起到一定的激励作用。因此这里测算出的最低生活保障线是合理的。

由民政部门提供的数据，江苏省各市执行的城镇居民最低生活保障线中，2008年最高的为330元，最低的只有200元，与预测结果相比，江苏省现行的城镇居民最低生活保障线是偏低的。

（3）从预测的趋势可以看出，最低生活保障标准是逐步增加的。其中2002～2003年的年间增长最慢，增长率仅为0.89%；2006～2008年的两年间的增长最快，增长率分别为4.11%和5.19%；2009～2015年间增长较平稳，年均增长率为2.50%。2002～2015年年均增长率为2.58%。

为了逐步提高贫困居民的生活水平，并且同时避免贫困面越来越大，给当地财政和社会稳定带来压力，政府应当制定最低生活保障线调整计划。政府可以根据预测增长率为基准，逐步提高最低生活保障标准，以满足贫困居民的基本需求，维持社会稳定。

[1]张思锋等.社会保障精算理论与应用[M].北京：人民出版社，2006.

[2]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002.

[3]骆祚炎.利用线性支出系统ELES测定贫困线[J].统计与决策,2006，(9).

[4]祝梅娟.贫困线测算方法的最优选择[J].经济问题探索，2003，（6）.

[5]李国柱，王劲涛，赖志花.对河北省城镇居民贫困线的测算[J].统计与决策，2005，(12).

[6]印飞，刘洋，顾晓瑜.基本养老保险基金需求预测研究[J].全国商情，2008，（19）.

O29

A

1002-6487（2011）04-0019-03

印凡成（1958-），男，江苏泰州人，副教授，研究方向：概率统计。

刘丽莹（1982-），女，河北石家庄人，硕士研究生，研究方向：应用数学。

黄健元（1964-），男，江苏溧阳人，教授，研究方向：社会保障。

（责任编辑/亦 民）