考虑价值漏损的风险投资项目实物期权定价方法
2011-10-24张宗益
鲁 皓,张宗益
(1.重庆大学 经济与工商管理学院,重庆 400030;2.重庆交通大学 理学院,重庆 400024)
考虑价值漏损的风险投资项目实物期权定价方法
鲁 皓1,2,张宗益1
(1.重庆大学 经济与工商管理学院,重庆 400030;2.重庆交通大学 理学院,重庆 400024)
与金融资产相比,实物资产本身往往具有现金流动性和持有收益率的特性,因此在对项目价值进行估价时,有必要考虑价值漏损的存在。文章在CA方法的基础上增加了对资产价值漏损的考虑,以二叉树模型为基础建立了包含价值漏损的实物期权定价方法。并通过算例将该方法与传统CA方法的计算结果进行了对比。
实物期权;MAD假设;二叉树;价值漏损
0 引言
风险投资是一种新兴的投资机制,是由风险投资家向投资者募集资金,对新兴的、迅速发展的、有巨大竞争潜力的企业注资,并在投资后提供管理经营等增值服务以使被投资企业能够迅速发展,最终获得高资本收益的投资行为。在风险投资过程中,投资家为了规避风险,往往会根据市场变化,灵活决定项目投资时间、规模和方式。这种相机选择行为赋予了风险投资家一种 “没有义务的权利”,Myers将这种权利定义为实物期权[1]。关于这些期权的价值分析因此构成风险投资决策的基础。
迄今为止,风险投资项目的实物期权定价方法主要可分为两类:一类是以Black Scholes公式为基础的连续时间模型。尽管这类模型理论上很完美,但在实际应用中往往会因为数学方法复杂、前提假设严格、结果不够直观而受到种种限制;另一类是以二项式期权定价模型为基础的离散型模型[2]。二项式期权定价模型将项目预期收益的变化近似地看成离散的随机游走过程,其优点在于简单直观,极限结果正好与著名的Black Scholes公式相符合,但是却存在着两个明显的缺点:一是由于每一节点仅有两种可能的状态,要获得较多的状态就必须不断地细分时间区间,增加结点,从而导致计算量迅速增大;二是需要找到同该资产完全相关的“孪生证券”以获得表示风险的波动率。为此许多学者又对二项式模型进行了扩展。Smith and Nau提出将二项式模型与决策树相结合[3](MNS方法),用二项式模型处理市场风险,用决策树模型处理技术风险。决策树的引入大大方便了模型的计算,但是在现实中市场风险和技术风险却往往难以区分;为解决这一问题,Copeland和Antikarov提出了更为通用的方法(CA方法),用不含柔性的项目现值作为标的风险资产的“孪生证券”(MAD假设),再根据对现金流的蒙特卡罗模拟分析获得综合反映项目风险的波动率,最后采用二叉树模型对实物期权定价[4]。在CA方法的基础上,Oriani和Sobrero结合风险投资项目多阶段投资的特征,构建了多阶段期权定价模型,并用模型分析了英国290家制造业企业的风险投资项目情况[5]。
然而,就作者所知,现有文献鲜有考虑实物资产可能产生的价值漏损问题。价值漏损是指期权合约持有者没有得到标的资产持有收益率和现金流的现象。目前的研究中实物期权价值多由动态复制方法决定,这种方法决定了在期权和复制组合之间不存在套利机会,因此价值漏损问题便无从考虑。但在实际上,很多实物资产都存在价值漏损现象(比如股利分红,利息等)。价值漏损的存在会改变标的实物资产价值的演化路径,从而影响到期权价值和项目价值[6]。因此本文针对标的资产的价值漏损情况,对CA方法进行了相应的调整,以期提高期权定价模型的准确性。
1 模型与评估方法
1.1 问题描述
风险投资公司拟分阶段投资于某项目。项目的投资有效期可划分为N个时长为△t的阶段,t阶段的投资为It。假设在△t内资产价值从起始值V分别以风险中性概率p和1-p随机移动到新值Vu和Vd,其中,r为无风险利率,则u>1,d<1,即从V到Vu是价值上升运动,而从V到Vd是价值下降运动。因此在t=1时项目价值只有一种可能V;在t=2时项目价值有两种可能状态Vu和Vd;t=i时,项目价值有种可能状态:
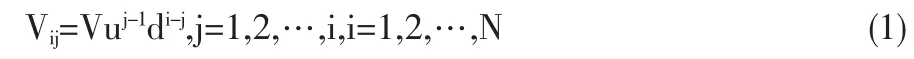
1.2 未考虑价值漏损的实物期权定价模型
Copeland和Antikarov提出了MAD假设,即用不含灵活性的现金流现值作为标的风险资产的“孪生证券”。并以此为基础,建立了通用的实物期权定价方法(CA方法)。该方法可分为如下四个步骤:
(1)通过DCF定价模型计算项目现值。第i期的项目价值为:,其中μ为风险调整贴现率,Ct为第i期的项目现金流。
(2)通过Monte Carlo法模拟项目收益,计算表示项目风险的波动率σ。
(3)根据各时期各状态下的项目价值得到资产价格二叉树。
(4)识别所有的实物期权,进行实物期权分析。从最后期间开始在每个节点上计算每个期权的价值,将期权价值与所需的投资比较,在每个节点标记最大值。再用复制技术沿决策树倒推,在树的起始点获得含有灵活性的项目价值。
CA方法的优点在于直观、灵活,在保留现金流折现分析外观形式的同时,还自然地列出了不确定性和或有决策的各种结果,并根据孪生证券的价值推演出期权价值。然而在实际工作中,由于价值“漏损”的存在,期权价值与孪生证券价值之间往往存在一定的偏差,从而影响到期权价值。因此在给项目定价的时候,有必要在期权定价模型中增加对价值漏损的考虑,以提高期权定价模型的准确性。
2 考虑价值漏损的实物期权定价模型
所谓价值漏损是指期权合约持有者没有得到标的资产的持有收益率和现金流的现象。多数实物资产都存在价值漏损,这些漏损要么以直接的现金流形式存在(如股利的分红、租金、利息),要么以隐含的持有收益率形式存在(如把持有的商品存货供应给市场得收益)。每当支付日来临时,这些现金流或便利收益会使得项目价值发生跳跃性的降低。因此为简化计算,可将价值漏损视为标定资产的比例部分。考虑到风险投资项目的进展管理是多阶段决策过程,可进一步设定该比例会随着阶段的变化而变化。这一设定是基于项目往往在不同时段呈现出不同特征的事实。实际上,产品成功推向市场需要往往要经历实验室研究阶段、中试阶段以及产品商业化阶段。每个阶段技术风险和市场风险会有不同的分布状况,此外,即使是相同的因素,在不同阶段的影响程度也不尽相同,因此项目往往会在不同时段呈现出不同特征。
为计算价值漏损,本文引入每个阶段的支付不变比率ki。由前分析知该比率只随着所处的时间阶段改变而改变,因此可将i阶段的支付不变比率定义为:ki=Ci/Vi。又因为价值漏损为标定资产的比例部分,比例取值与状态j的取值无关,只随着所处的时间阶段改变而改变,则i期j状态下价值漏损Cij=kiVij。
CA方法中,资产价格二叉树是由各时期各状态下的项目现值得到的(Step3)。而本文拟用价值漏损和各时期各状态下的项目现值来构造资产价格二叉树,构造步骤如下:
第一步:计算扣除价值漏损后的项目价值Vij':
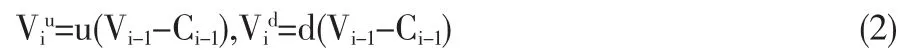
(2)式中u,d表示价值的上升下降程度,Vi-1表示前一阶段的项目价值,Ci-1=ki-1Vi-1表示上期价值漏损(在上期期末所支付的现金流),这将减少后续各期的项目价值。特别地,当阶段i=0时,因为项目还未启动,没有产生价值漏损,故k0=0;当阶段 i=1 时,有=uV0,=dV0,此时本文的方法与 CA方法是一致的。
第二步:计算各时期各状态下扣除价值漏损后的项目现值Vij'':

第三步:计算各时期各状态下的价值漏损现值:

第四步:计算各时期各状态下的项目现值Vij:

由(4)、(5)式可以得到二叉树的各分叉值,从而可以构造资产价格二叉树。然后在此基础上识别所有的实物期权,建立期权决策树进行实物期权分析。在进行实物期权识别分析时,要注意将价值漏损加入项目价值中。以放弃期权为例,若用CA方法,则应当从最后期间开始计算每个节点上包含期权的项目现值为V=max{VNj,K},K为期权执行价格。然后用复制技术沿决策树倒推,在树的起始点获得含有灵活性的项目价值;而用本文提出的包含价值漏损的二叉树期权定价模型,最后期间每个节点上包含期权的项目现值为V=max{VNj,VNj-VNj''(1-kN)+K/(1+r)N}。
3 数值算例
以玉石矿开发为例[7]来分析含有价值漏损的实物期权定价模型在价值评估中的应用。A公司拟投资一个玉石矿开发项目,预计需要投资900万元。矿石的产量每年约29吨,并可以较长时间维持不变;该种玉石的价格目前为每吨10万元,预计每年上涨11%,其标准差为35%,固定成本每年100万元。风险调整贴现率为10%,无风险利率为5%,项目波动率σ=35%,第3年时企业可以400万元的残值放弃开发。按照DCF定价模型计算项目现值,并计算每期的现金流支付比率ki如表1所示:
再取△t=1,则有u=1.419,d=0.705,风险中性概率p=0.483。用CA方法和含价值漏损的实物期权定价模型对玉石矿项目进行估值的过程分别如下:
3.1 CA方法的估值过程
根据最初的项目价值和上升下降比率可以得到各状态下的资产价值,将资产价值作为分叉值,则可得到资产现值变化树形图如图1所示。在第3年,企业可决定继续进行项目或者选择放弃期权。因此可在树形图的基础上,在第3年处插入决策点用以表示项目可执行的期权。第3年末含期权的项目现值为VO3j=max(V3j,400/(1+0.05)3),而第2年末至第1年末的项目现值可根据风险中性概率逐年向前递推。从而得到含有灵活性的项目价值为881。这表明,初始投入900万元的研发投资,可得到该研发项目包含实物期权在内的项目超额收益价值为-19万元。
3.2 考虑价值漏损的估值过程
根据(4)、(5)式计算价值漏损 Cij'和项目现值 Vij,求得资产现值变化树形图如图2所示。在给定事件树的前提下,再在第三年插入决策点用以表示项目在第3年可执行的期权,实物期权分析过程如图3所示。在第3年,企业可决定继续进行项目,或者选择放弃期权。令第3年末不执行期权的项目现值为V3j,包含放弃期权的项目现值A3j。第3年末含期权的项目现值为 VO3j=max(V3j,A3j),其中A3j=V3j-V3j''(1-k3)+400/(1+0.05)3。第2年末至第1年末的项目现值,可根据风险中性概率逐年向前递推。从而在决策树的起始点获得含有灵活性的项目价值为1009。这表明,初始投入900万元的研发投资,可得到该研发项目包含实物期权在内的项目超额收益价值为109万元。
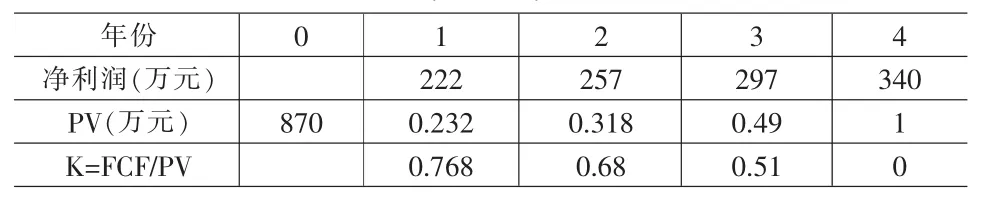
表1 企业预计现金流,净现值,现金流支付比率
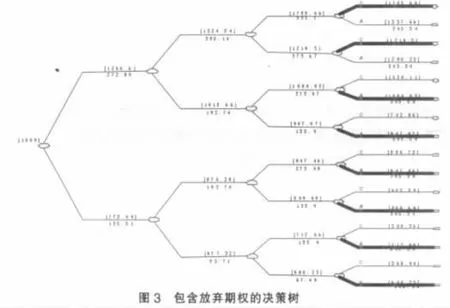
根据以上分析可以看出,传统DCF法的计算结果比实物期权方法的计算小,这可以解释为DCF法忽略了管理柔性,从而造成的投资机会价值的低估;对比两种实物期权方法可以发现,考虑价值漏损的实物期权估值要比通过CA方法计算出来的项目估值大128万元,这个偏差是比较大的。如果将价值漏损类比为股票红利,标的资产类比为股票,放弃期权类比为看跌期权,则可以在股票市场中找到与本文类似的偏差现象:股票市场中,红利的发放将使得股票的价格降低,从而增加看跌期权的价值,减少看涨期权的价值。因此由数值算例可以发现,与CA方法相比,含有价值漏损的实物期权定价反映了影响期权价值的实体资产真实回报的变化情况,如果忽视了这些调整将可能导致期权估价错误并可能误导投资决策。
4 结语
由于现金流和便利收益的存在,实物资产往往存在着价值漏损的现象,传统的实物期权定价方法往往忽视了这一点。本文针对这一不足,在CA方法的基础上增加了对资产价值漏损的考虑,并以二叉树模型与决策树为基础建立了一个包含价值漏损的实物期权定价方法。并通过一个应用实例,将所建立的方法与传统CA方法的计算结果进行了对比。实验结果表明,含有价值漏损的实物期权定价模型更能反映影响期权价值的实体资产真实回报的变化情况。
本文所构建的模型保持了二叉树模型的实用性和灵活性:一方面,计算程序编写和参数调整都非常直观方便,并不需要大量复杂的数学计算过程;另一方面,模型能提供详细的模型化决策过程,能够清楚反映出期权存在期间的最优决策路径。模型适用于已完成市场调查,已对未来现金流情况做出估计的R&D项目,也适用于自然资源开发项目和房地产开发项目。
价值漏损的成因是现金流或便利收益,本文只讨论了现金流的情况,而对便利收益的讨论还未涉及。因此对便利收益的研究将是一个尚待深入的方向。
[1]Smith J.Decision Analysis in Management Science[J].Management Science,2004,(50).
[2]John Hull.Options,Futures and other Derivatives (7thEdition)[M].NJ:Prentice Hall,2008.
[3]Smith J,Nau R.Valuing Risky Projects:Option Pricing Theory and Decision Analysis[J].Management Science,1995,14(5).
[4]Copeland T,Tufano P.A Real-World Way to Manage Real Options[J].Harvard Business Review,2004,82(3).
[5]Orinai R,Sobrero M.Uncertainty and the Market Valuation of R&D within a Real Options Logic[J].Strategic Management Journal,2008,29.
[6]Andrew Metric.Venture Capital and the Finance of Innovation,[M].USA:RDC Publishing,2010.
[7]王琳,杨方文.EXCEL在放弃期权计算分析中的运用[J].研究与探索,2008,(4).
[8]李川,邓光军,曾勇.技术创新与增长期权定价[J].运筹与管理,2003,(6).[9]毕守锋,李岱松,马欣.复合期权方法在项目评估中的应用[J].科研管理,2008,(3).
[10]张矢的,魏东旭.风险投资中双重道德风险的多阶段博弈分析[J].南开经济研究,2008,(6).
[11]郭菊娥,晏文隽,张国兴.风险投资主体对高新技术企业分阶段投资的时机选择[J].系统工程理论与实践,2008,(8).
F224
A
1002-6487(2011)04-0054-03
国家自然科学基金资助项目(70941029);重庆交通大学青年科学基金资助项目
鲁 皓(1980-),女,重庆人,博士研究生,研究方向:技术创新与风险管理。
张宗益(1964-),男,贵州人,教授,博士生导师,研究方向:公司治理与技术创新。
(责任编辑/亦 民)
