基于偏相关系数和平行检验的主成分抽取数量的确定方法

尹 波

（成都东软学院，成都 611481）

基于偏相关系数和平行检验的主成分抽取数量的确定方法

尹 波

（成都东软学院，成都 611481）

主成分抽取数量的确定是主成分分析中的关键问题。文章提出了一种新确定方法：首先基于原样本数据采用偏相关系数准则来确定主成分抽取的数量；然后基于再抽样样本数据来验证主成分数量模型的稳定性，并在SPSS环境下实现了该方法。实例应用表明该方法相比特征值大于1、Cattle Scree等准则，结果更客观、准确和稳定，可广泛应用于主成分分析、因子分析等相关研究中。

主成分抽取数量准则；特征根大于1；偏相关系数；平行检验

0 引言

在管理科学的研究中，经常需要通过问卷调查等方式来获得样本数据，并对样本数据进行主成分抽取或因子抽取（以下统称主成分抽取）时，这里必然要涉及的一个重要问题就是主成分抽取数量的确定[1，2，3]。不少研究者常常采用SPSS或SAS软件包中内置的降维模块来确定主成分抽取的数量，并进而构建结构模型。比如SPSS15.0 for Windows中确定主成分抽取数量的准则主要有两个：一是特征根大于1；二是预先确定要抽取的主成分数量。由于常常预先难以确定主成分抽取的数量，国内不少研究者是采用特征根大于1的抽取准则（Kaiser准则）[4，5，6，]，以《管理世界》为例，2001～2006 年涉及主成分和因子抽取的文章36篇，其中使用Kaiser准则的32篇。事实上，Kaiser准则作为主成分抽取的常用准则[7]，往往过多地抽取主成分[2，3]，导致部分主成分难以赋予合适的意义，成为“噪音”；或采用解释总方差比例（比如大于85%）作为主成分抽取的准则[8]。这些方法不免主观和武断，缺乏足够的科学依据。

由于Kaiser准则等的不足，国内外不少学者对于主成分抽取数量确定的准则作了研究和改进。比如Cattell Scree准则，是通过观察Scree Plot图形的“肘部”来判断主成分抽取数量的一种直观方法，该准则可以提高主成分确定数量的准确性，但存在的问题是有时候“肘部”不容易清楚判断或者有几个“肘部”[9]；文献[10、11]在探索性阶段预先确定主成分数量的备选范围，在验证性阶段检验主成分数量和相应结构模型，较好地提高了主成分数量确定的科学性和相应结构模型的稳定性，但这些方法还存在以下问题：一是备选主成分数量如何有效确定；二是模型的吻合情况只针对了样本数据，得到的主成分数量模型对于总体数据而言可能有一定甚至较大的偏差。

基于以上研究，本文拟提出确定主成分抽取数量的新方法：首先基于原样本数据采用Velicer偏相关系数准则来确定主成分抽取的数量；然后基于再抽样样本数据采用Horn平行检验来验证主成分数量模型的稳定性，并在SPSS环境下编程实现了该方法。该方法将较好地解决文献[4、5、6、8、10、11]方法中存在的问题，在样本数据一定的情况下，可减少主成分数量模型的系统误差，提高模型的泛化性和稳定性，是对目前广为使用的Kaiser准则等的改进，可应用于主成分分析和因子分析等相关研究中。

1 主成分抽取数量确定的方法

主成分抽取的目标是以尽可能少的主成分来尽可能充分地反映原样本空间的信息。主成分数量抽取太少，就难以充分地反映原有信息。主成分抽取数量过多，反映的原样本空间信息多，但较多的主成分难以给予恰当的背景意义。“尽可能少”的主成分和“尽可能多”信息之间的平衡是主成分抽取的关键和困难所在。这里我们提出确定主成分抽取数量的新方法，其步骤为：

（1）基于样本数据，选择良好的判断准则，确定主成分抽取的数量。

（2）采用同一总体数据中不同样本数据，选择良好的检验方法，对（1）所确定的主成分数量模型进行检验。

（3）如检验通过，主成分数量模型确定；如检验未通过，寻找其他方法来确定主成分数量。

1.1 基于样本数据的Velicer判别准则

目前基于样本数据的判别准则多样，如Kaiser准则、Cattle Scree准则、解释的总方差比例、Bartlett's Sphericity检验和Velicer偏相关系数等。从算法的理论基础、目标、主成分数量结构的显著性等方面来考察，不同的准则有不同的优缺点，总体而言，Velicer偏相关系数作为一种对于数据分布无假设、统计计算量不大的统计方法，是普遍公认的最好方法[12、13]，其方法可以表述为：

设向量矩阵X=(x1，x2，…，xp)，从X中抽取m个主成分Z=(z1，z2，…，zm)。 矩阵[X，Z]的相关系数矩阵为这里C11是X的相关系数矩阵，C22是Z的相关系数矩阵，从向量矩阵 X=（x1，x2，…，xp）中去除 m 个主成分所得矩阵的相关系数矩阵为

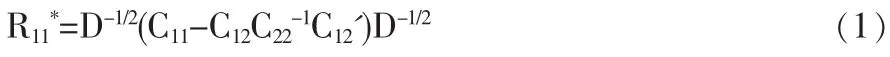
这里rij*是矩阵R11*第i行和第j列的元素。当fm的值最小时，对应的m的值即抽取的主成分数量，这里m取值从1到p-1。2000年Velicer,W.F.等对于最小平均平方根偏相关系数准则进行了改进，提出了最小平均1/4次方偏相关系数准则，基于真实数据和仿真数据的研究表明两种最小平均偏相关系数检验结果极其相似，但后者更加准确和灵敏[14]。

1.2 基于同一总体数据中不同样本数据的检验

如果样本数据充分，我们可以从全体样本数据中随机抽取一些样本数据用于主成分分析来确定抽取的主成分数量（通常是总样本数据的2/3），另外一部分数据用于主成分数量模型的检验。实际应用中，通常样本数据较少，因此需要我们采用Bootstrap方法产生再抽样数据进行主成分数量模型的检验。

基于再抽样样本数据的检验方法我们选择Horn平行检验。Horn平行检验首先计算再抽样样本集合的特征值的平均值λmean，并与基于原样本数据的特征值λraw分布相比较，观察λraw≥λmean，对应的主成分数量的最大值就是最优决策；进一步考虑在 95%置信区间下的 λm，比较 λm与 λraw，观察 λraw≥λm，对应的主成分数量的最大值就是更稳定的主成分数量决策[15、16]，这也是美国教育与心理测量杂志大力推广的确定主成分抽取数量的方法[17]。这个方法的缺点是再抽样数据在某种意义上而言是伪数据，特别是当抽样调查方法不尽科学合理时，数据的偏差会更大。单一使用Horn平行检验来确定主成分抽取的数量有较大的样本风险，因此我们仅仅使用Horn平行检验来验证基于原样本数据所确定的主成分数量模型。

1.3 检验通过或未通过的情形

如检验通过，主成分数量模型确定；如检验未通过，需要寻找其他方法，如Bootstrap Bias Corrected and Accelerated（BCa）等更复杂的模型来寻找最优解[18，19]。

综合1.1，1.2，1.3所述，我们确定主成分抽取数量的方法为：

（1）基于样本数据，选择Velicer偏相关系数准则，确定主成分抽取的数量。

（2）基于Bootstrap再抽样样本数据，选择Horn平行检验，对（1）确定的主成分数量模型 进行检验。

（3）如检验通过，主成分数量模型确定；即同时满足公式（3）、（4）的解为要抽取的主成分数量。

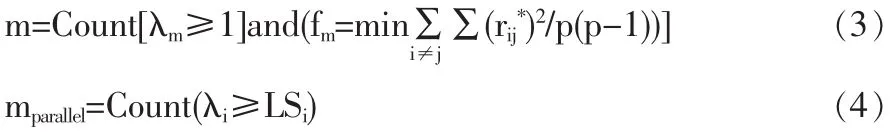
这里λi是基于原样本数据的第i个特征值，LSi是对应第i个特征值的基于Bootstrap再抽样数据的特征根均值或95%的置信区间的统计值等。如联立公式（3）、（4）无解，需要寻求其他方法如BCa等来确定主成分抽取数量。

由于Kaiser准则、Cattle Scree准则、解释的总方差比例等都可以通过统计软件SPSS来实现，因此我们选择在SPSS环境下编程实现Velicer偏相关系数准则和Horn平行检验来完整实现该方法。

接下来，我们应用这一方法对笔者的一次国际酒店企业文化调查问卷确定需要抽取的主成分抽数量，并与Kaiser准则、Scree碎石准则、解释的总方差比例等通行方法做一个比较，以检验该方法的可行性和有效性。

2 应用

2006～2007年期间笔者对成都一国际酒店进行了一次企业文化问卷调查。调查问卷发放过程中尽可能覆盖各个部门，不同年龄、不同性别和不同层次等等，得到一个50×15的样本矩阵。在对问卷调查进行主成分分析前，首先我们观察变量间相关系数矩阵（Correlation Matrix），可知不少变量之间存在高度相关；其次观测KMO值和 Bartlett球型检验情况，KMO值为0.869，说明目前的变量能够较好地被主成分所解释。Bartlett Sphercity检验拒绝单位矩阵的假设，检验结果表明问卷数据适合做主成分分析。

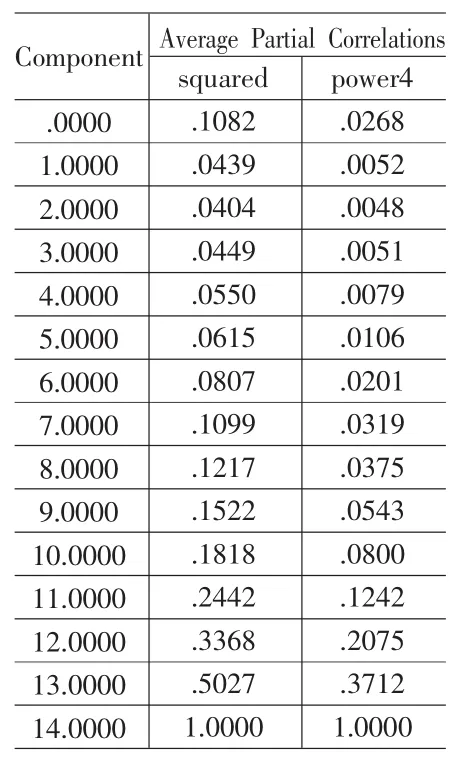
表1 Velicer偏相关系数

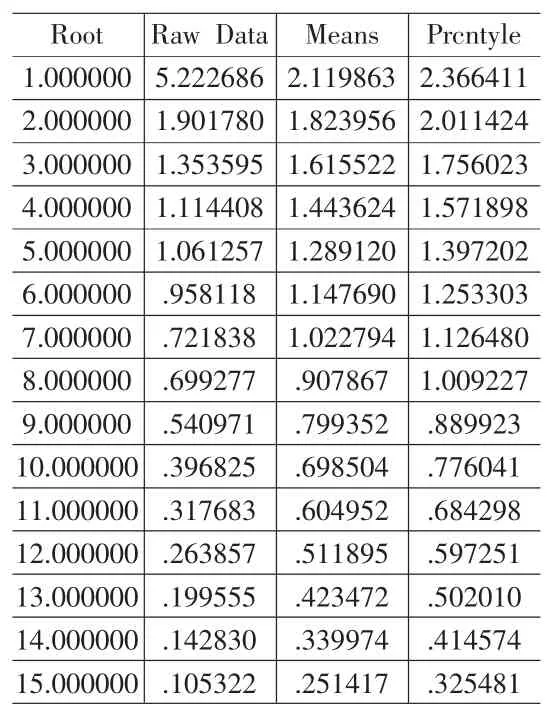
表2 原样本数据特征值&再抽样样本数据特征值均值 &95%置信区间下的特征值均值

2.1 基于样本数据的主成分抽取数量的确定

我们采用Velicer 偏相关系数准则来求解主成分数量，结果如表1所示。最小平均平方根偏相关系数是0.0404，抽取的主成分数量为 2；最小平均1/4次方偏相关系数是0.0048，也说明抽取的主成分数量应为2。

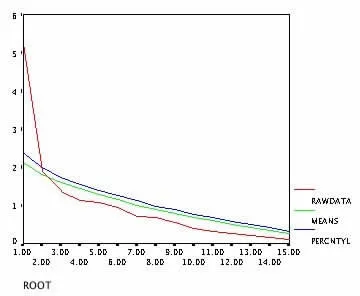
图1 基于原样本数据和再抽样样本数据的主成分数量

2.2 基于再抽样样本数据的检验

本文采用Bootstrap方法生成再抽样样本数据1000组，应用Horn平行检验来加以验证，结果如表2和图1所示。

基于1000组再抽样样本数据，确定应抽取2个主成分。检验结果表明：基于原样本数据的Velicer偏相关系数准则所确定的主成分数量模型（2个主成分）具有良好的稳定性和泛化性。另外图1中的RAWDATA曲线就是Scree Plot图，从该曲线可以观察出，曲线的肘部在主成分数量为2处；如采用Kaiser准则，应抽取5个主成分。进一步验证了文献[2、3]等指出的kaiser法则过多抽取主成分和文献[2、12、13]等指出的基于样本数据的判别准则Velicer偏相关系数是最好的结论。综合以上分析，可以得到表3。

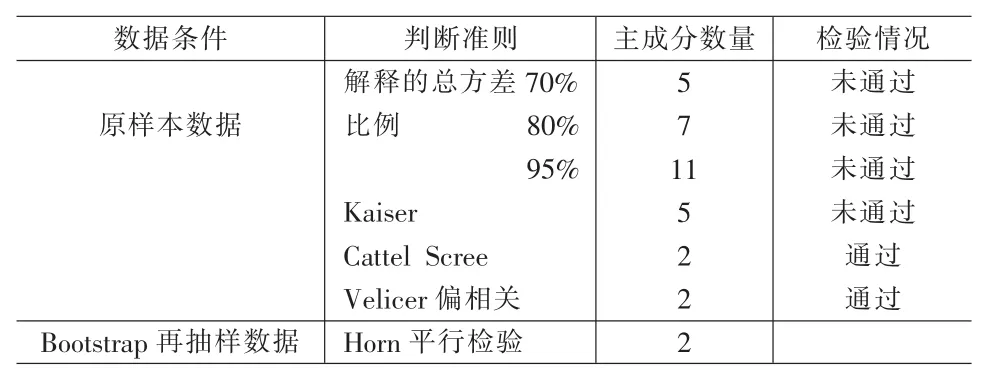
表3 不同判断准则得出的主成分数量①限于篇幅，特征根解释的总方差比例直接给出。

3 结论

本文针对当前主成分抽取数量确定方法中广泛使用的特征值大于1、解释的总方差比例、Cattle Scree等准则所存在的一些不足，提出了一种新的确定方法。该方法首先基于样本数据采用Velicer偏相关系数准则来确定主成分抽取的数量，然后基于Bootstrap再抽样数据采用Horn平行检验来验证主成分数量模型的稳定性，并在SPSS环境下实现了该方法。

本文应用该方法对笔者的一次国际酒店企业文化调查问卷确定主成分抽取的数量，结果表明相比特征值大于1、解释的总方差比例、Cattle Scree等方法，本文所得结论更客观、准确和泛化；进一步支持文献研究关于Kaiser准则过多抽取主成分的结论。

本文提出的方法是对目前特征值大于1等准则的改进，可广泛应用于主成分分析、因子分析等相关研究中。

[1]Franklin,S.,Gibson,D.,Robertson,P.,Pohlmann,J.,Fralish,J.Parallel Analysis:A Method for Determining Significant Components[J].Journal of Vegetation Science，1995，(1).

[2]Jackson D.Stopping Rules in Principal Components Analysis:a Comparison of Heuristical and Statistical Approaches[J].Ecology,1993,(8).

[3]Rencher,A.Multivariate Statistical Inference and Applications[M].New York:John Wiley&Sons Inc,1998.

[4]王国顺,张仕璟,邵留国.企业文化测量模型研究——基于Dension模型的改进及实证[J].中国软科学,2006,(3).

[5]任胜钢,彭建华.基于因子分析法的中国区域创新能力的评价及比较[J].系统工程,2007,(2).

[6]黄善东,杨淑娥.公司治理与财务困境预测[J].预测,2007,(2).

[7]Kaiser,H.F.The Application of Electronic Computers to Factor Analysis[J].Educational and Psychological Measurement,1960,(1).

[8]贺颖.2001～2004年中国管理类期刊学术影响力综合评价[J].中国软科学,2007,(1).

[9]Cattell B.The Scree Test for the Number of Factors[J].Multivariate Behavioral Research,1966,(2).

[10]柯江林,孙键敏,石金涛,顾琴轩.企业R&D 团队之社会资本与团队效能关系的实证研究[J].管理世界,2007,(3).

[11]唐炎华,石金涛.我国知识型员工知识转移的动机实证研究[J].管理工程学报,2007,(1).

[12]Velicer W.Determining the Number of Principal Components from the Matrix of Partial Correlations[J].Psychometrika,1976,(3).

[13]Ferre L.Selection of Components in Principal Component Analysis:A Comparison of Methods[J].Computational Statistics and Data Analysis,1995,(6).

[14]Vellcer,W.F.,Eaton,C.A.,Fava,J.L.Construct Explication Through Factor or Component Analysis:A Review and Evaluation of Alternative Procedures for Determining the Number of Factors or Components[A].Problems and Solutions in Human Assessment[M].Boston:Kluwer,2000.

[15]John L.,Horn.A Rationale and Test for the Number of Factors in Factor Analysis[J].Psychometrica,1965,(2).

[16]Glorfeld,L.W.An Improvement on Horn’s Parallel Analysis Methodology for Selecting the Correct Number of Factors to Retain[J].Educational and Psychological Measurement,1995,(3).

[17]Thompson,B.,Daniel,L.G.Factor Analytic Evidence for the Construct Validity of Scores:A Historical Overview and Some Guidelines[J].Educational and Psychological Measurement,1996,(2).

[18]Efron,B.Better Bootstrap Confidence Intervals[J].Journal of the American Statistical Association,1987,(3).

[19]Hall,P.Theoretical Comparison of Bootstrap Confidence Intervals[J].The Annals of Statistics,1988,(3).

F222

A

1002-6487（2011）04-0007-03

尹 波（1971－），男，江西吉安人，博士，教授，研究方向：组织文化与计量管理。

（责任编辑/亦 民）