不同风况和系统容量下双馈风机并网谐波特性研究

熊来红，单瑞卿，汪皓钰，刘会金，刘勇

（1.武汉大学电气工程学院，湖北武汉430072；2.河南省电力公司洛阳供电公司，河南洛阳471009）

风力发电系统主要有恒速恒频和变速恒频系统，恒速恒频风力系统是通过浆距控制使得异步机转子转速恒定，得到恒压恒频的电能然后并网，这种系统没有电力电子装置，谐波含量少；而双馈风力发电机因其风力机变速运行，可以在很宽的风速范围内保持近乎恒定的最佳叶尖速比，从而提高了风力机的运行效率，是当今风电场主流风力发电机型。

双馈风力发电机产生的谐波主要来自两方面：一方面是发电机气隙空间谐波磁势，这种谐波含量较少，对电网电能质量影响有限；另一方面是来自连接于转子上的AC-DC-AC变流器，因其一般采用SPWM调制控制方式，而三角载波频率极高，因而不可避免地会产生高次谐波，这是风力发电系统谐波的主要来源，在转子中的谐波电流还会通过定子放大注入电网，对电能质量造成不可忽视的危害，必须加以治理。

双馈风力发电机时刻处在不断变化的风速之中，变流器为了使得发电机定子侧电压频率恒定，控制系统必须适时随风速的变化来调整控制脉冲，控制变流器输出转子励磁电流频率，达到变速恒频的控制目标。因此，在不同的风速下，变流器的运行状态将呈现出不同的状态，变流器的这种变化也必将对风电场并网谐波特性产生影响。

本文利用MATLAB/Simulink，选择了适用于研究双馈风力发电机并网谐波特性的详细系统模型，并对电网侧做了适应性修改，此外，根据通用的风速四分量模型，即基本风、阵风、随机风、渐变风，基于MATLAB构建了风速四分量仿真模型，最后，搭建了反映风机并网谐波特性的数据测量系统，最终完成风机并网全系统仿真模型，仿真过程中，针对双馈风力发电机并网系统在不同风速分量模型、不同电网容量情况下，风电场对电网各母线、电流的畸变率进行了仿真研究，得出双馈风力发电机并网的谐波特性，对风电场并网带来的电能质量问题有一定指导意义。

1 风力发电系统数学模型

1.1 四分量风速模型

风速模型可以看成是由基本风、随机风、渐变风和阵风叠加而成，下面分别建立四分量风速的数学模型。

1）基本风。是指根据风电场长期测得的风速数据，采用极大似然估计法得到风电场风速Weibull分布参数，然后就可以计算出基本风速V1。

2）阵风。阵风是突然变化的风速过程，容易引起明显的电网电压波动，具有三角余弦函数特性，数学模型如下：

3）渐变风。对风速以一定速度逐渐上升时，这种风况可以用渐变风速模型来模拟，数学模型如下。

式中，Rmax为渐变风最大值；T1r为风速渐变开始的时间；T2r为风速渐变结束的时间；Tr为渐变风保持时间。

4）噪声风。噪声风用来描述自然风时刻随机变化特性的过程，其表达式为

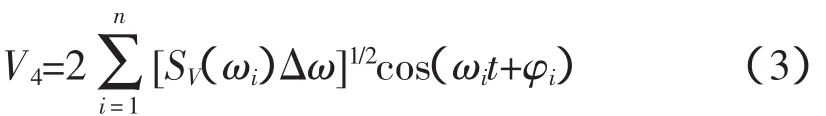
式中，ωi是第i个分量的角频率；Δω为随机分量的离散间距；φi为在0~2π之间服从均匀概率密度分布的随机变量；SV（ωi）为第i个随机分量的振幅。

1.2 并网双馈风力发电机数学模型

由于双馈发电机在传统三相坐标系下的数学模型存在磁路上的耦合，其有功、无功相互耦合，为了达到有功功率、无功功率解耦控制的目的,采用了矢量控制。矢量控制是基于d-q坐标系统的，因此必须研究双馈发电机在d-q坐标系下的数学模型。很多文献已经得出了双馈发电机三相坐标系下的数学模型，下面经过Park变换直接给出其d-q坐标下的数学模型。

定子绕组电压方程；

转子绕组电压方程：

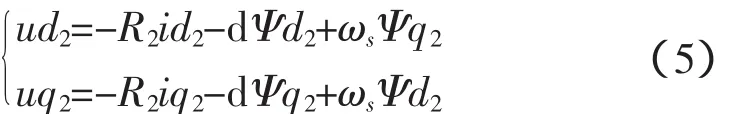
定子磁链方程：

转子磁链方程：

转矩方程：

运动方程：

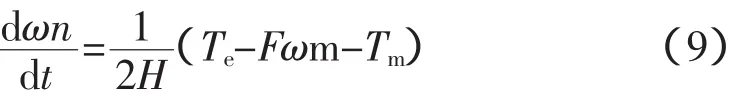
式（4）—（9）中，d表示微分算子d/d t；R1是发电机定子等效电阻；R2是转子等效电阻；ω1是同步转速；ωs是转速差（等于同步转速减去转子转速）；L1是发电机定子等效自感；Lm是定转子互感；L2是转子等效自感；ωm是转子旋转机械角速度；F是阻力；Te是发电机电磁转矩；Tm是机械转矩；u表示电压；i表示电流；Ψ表示磁通量。

2 不同风速和不同系统容量对谐波特性的影响

2.1 不同风况对并网谐波特性的影响

在不同风况作用下，风电的控制系统会不断调整双变流器触发脉冲，实现网侧变流器单位功率因数运行和维持直流侧电压恒定，机端变流器通过定磁链控制达到双馈机输出无功、有功解耦控制目标。因此，不同风况下，变流器运行状态不同，谐波特性将不同，后面将进行仿真研究。

2.2 不同系统容量对并网谐波特性的影响

在研究风电场并网的谐波特性时，将风电场视为一谐波源，以图1所示等效电网结构图为例说明短路容量对谐波潮流的影响。

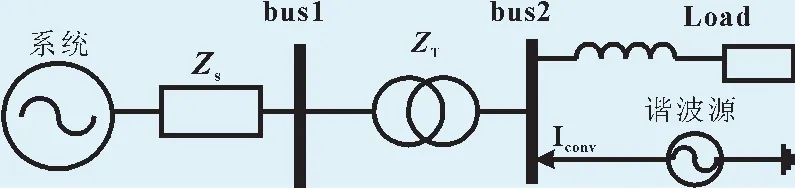
图1 谐波源注入电网等效电路Fig.1 Equivalent circuit of harmonic source inputting

可以看出，当系统容量变大时（等效为Zs变小），则从谐波源看进去的等效电阻变小，即Z eq（h）=Zs（h）+ZT（h）变小，由公式Vbus2（h）=Z eq（h）*I conv（h）得，Vbus2（h）变小，即bus2的电压畸变率变小，而bus1的谐波电压可由下面公式算出：

可见，系统容量大，可以降低母线谐波畸变率，谐振时，使得谐振频率向更高方向移动，谐振时的系统阻抗模值也减小。图2所示为仿真整体框图。

3 仿真分析

3.1 仿真平台的搭建

仿真是基于MATLAB中的风电场并网平台，MATLAB中有3种风电场并网的Demo，分别是Detailed model，Average model，Phasor model，分别适合于不同的研究目的，本文选择适合研究风电场谐波的Detailed model，并对其参数进行修改，使其符合我国电网实际，其电网结构是1台1.5 MW的风机并网，电网容量40 MVA，风电场出口电压为690 V，然后通过35 kV电网与110 kV电网相连。然后搭建了四分量风速生成模型及整个电网的谐波测量分析平台。

3.2 四分量风速仿真模型

基于四分量风速数学模型搭建了仿真模型，可以输出渐变风、阵风、随机风、基本风等风速分量。仿真框图如图3所示。

图2 仿真整体框图Fig.2 The frame of Simulation diagram

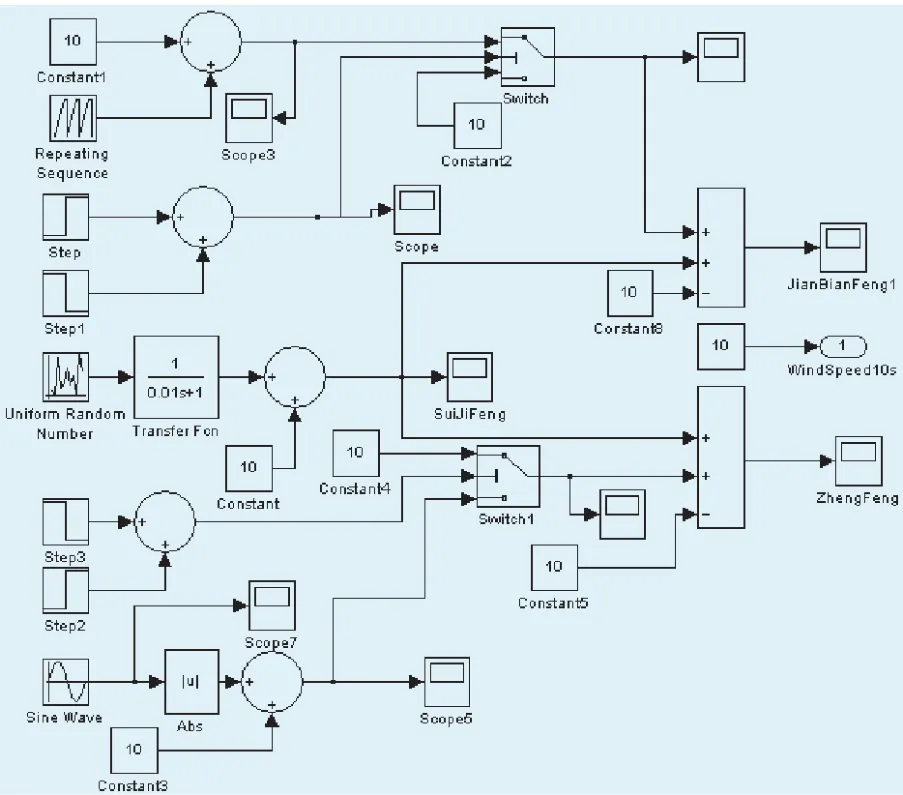
图3 四分量风速仿真模块Fig.3 Simulation module for four components wind

3.3 仿真分析

设置在不同的风况下，对风机并网所带来的谐波进行仿真，得出了不同风况下的谐波在电网中的分布，各个母线的电压畸变率等。由于高些谐波幅值很小，所以本仿真中的谐波次数只分析50次以下且幅值大于基波的0.5%的谐波含有情况。

3.3.1 恒定额定风速下谐波仿真分析

设风速保持10 m/s，仿真时间为10 s，FFT分析时间段为（4 s，5 s），仿真波形如图4—图7所示，图8所示为叠加随机风的阵风风速。

3.3.2 阵风速下的谐波仿真分析

仿真条件：构建一基于基本风的阵风模型，最大幅值15 m/s，持续时间4 s，为使分析更具针对性，在做FFT分析时，只分析电流波形幅值变化较大的（5.5 s，6.5 s）这个时间段内幅值大于0.5%的谐波形数据，结果如图9—图14所示。

图4 690 V母线电流THDFig.4 The electric current THD of 690 V Bus

图5 690V母线电压THDFig.5 The voltage THD of 690 V Bus

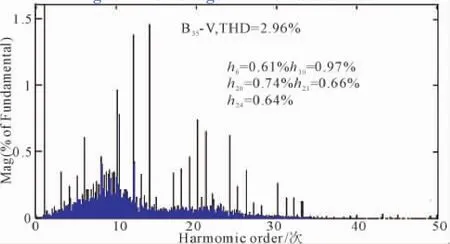
图6 35 kV母线电压THDFig.6 The voltage THD of 35 kV Bus

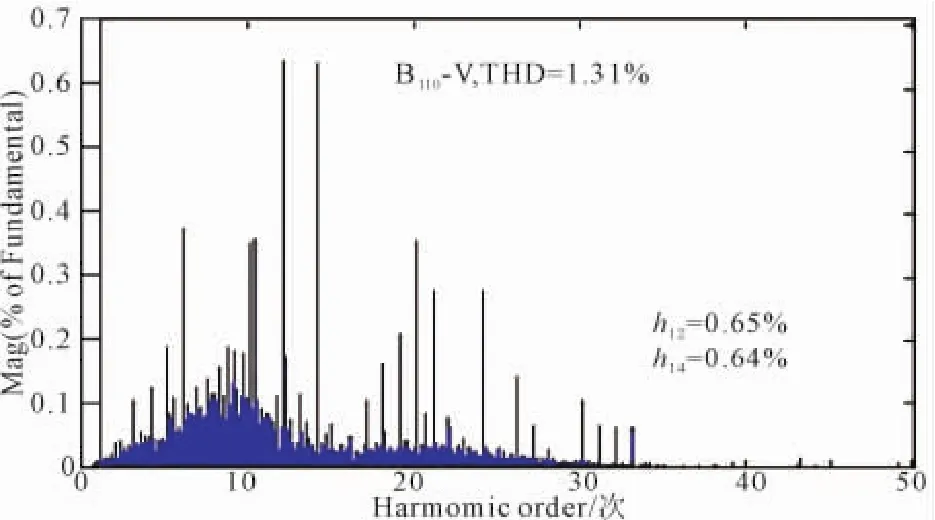
图7 110kV母线电压THDFig.7 The voltage THD of 110 kV Bus

图8 叠加随机风的阵风风速Fig.8 Gust wind plus random wind

3.3.3 渐变风速下的谐波仿真分析

仿真1：构建基本风速+随机风的渐变风，风速在3 s内由10 m/s上升到15 m/s，用FFT分析了（5.5 s，6.5 s）时间段波形的谐波畸变率，波形如图15—图18所示。

图9 690 V母线电流波形Fig.9 The electric current of 690 V Bus

图10 690 V母线电流THDFig.10 The electric current THD of 690 V Bus

图11 690 V母线电压THDFig.11 The voltage THD of 690 V Bus

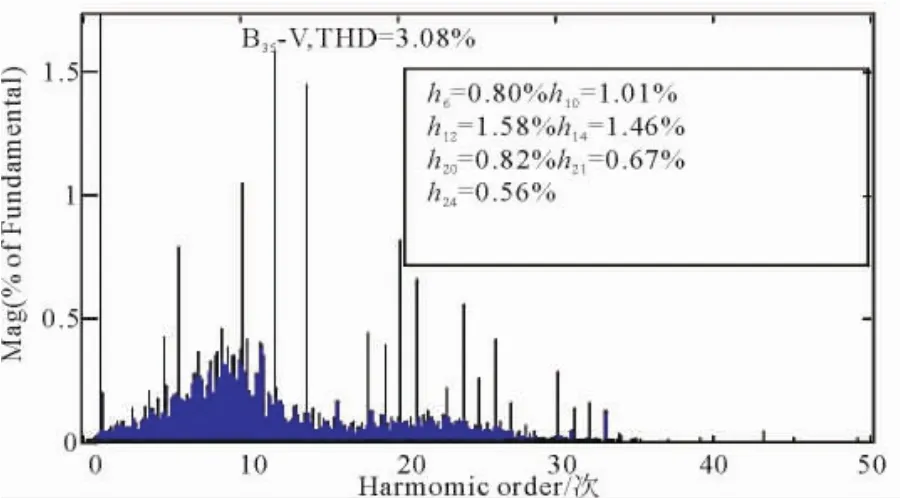
图12 35 k V母线电压THDFig.12 The voltage THD of 35 kV Bus

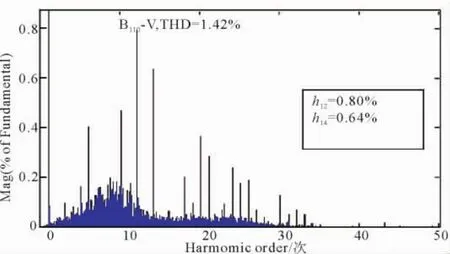
图13 110 k V母线电压THDFig.13 The voltage THD of 110 kV Bus

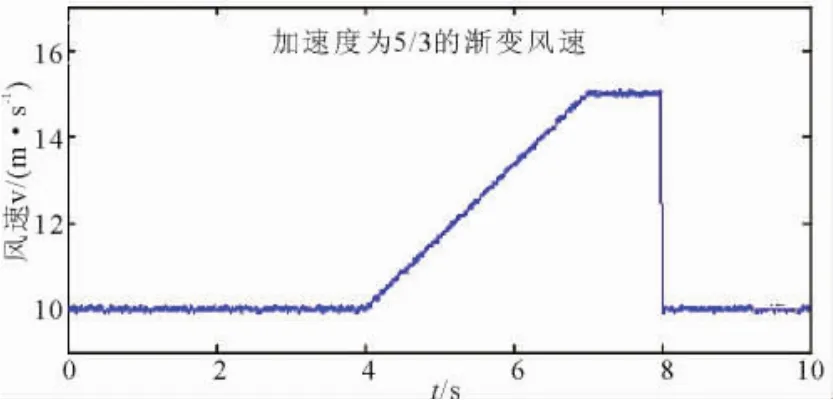
图14 基本风+随机风Fig.14 Basic plus random wind

图15 690 V母线电流THDFig.15 The electric current THD of 690 V Bus

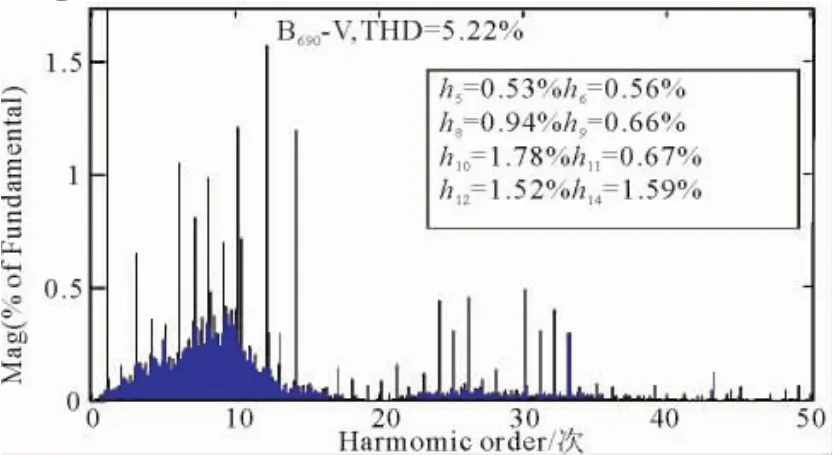
图16 690 V母线电压THDFig.16 The voltage THD of 690 V Bus

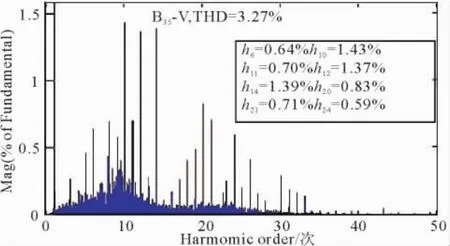
图17 35 kV母线电压THDFig.17 The voltage THD of 35 kV Bus

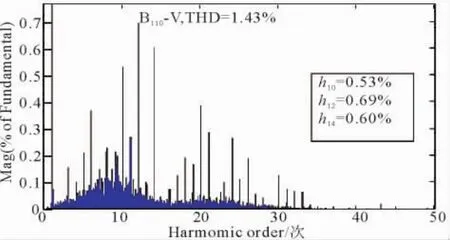
图18 110 kV母线电压THDFig.18 The voltage THD of 110 kV Bus

仿真2：构建基本风速+随机风的渐变风，风速在1 s内由10 m/s上升到15 m/s,用FFT分析了（4 s,5 s）时间段波形的谐波畸变率，波形如图19—图23所示。

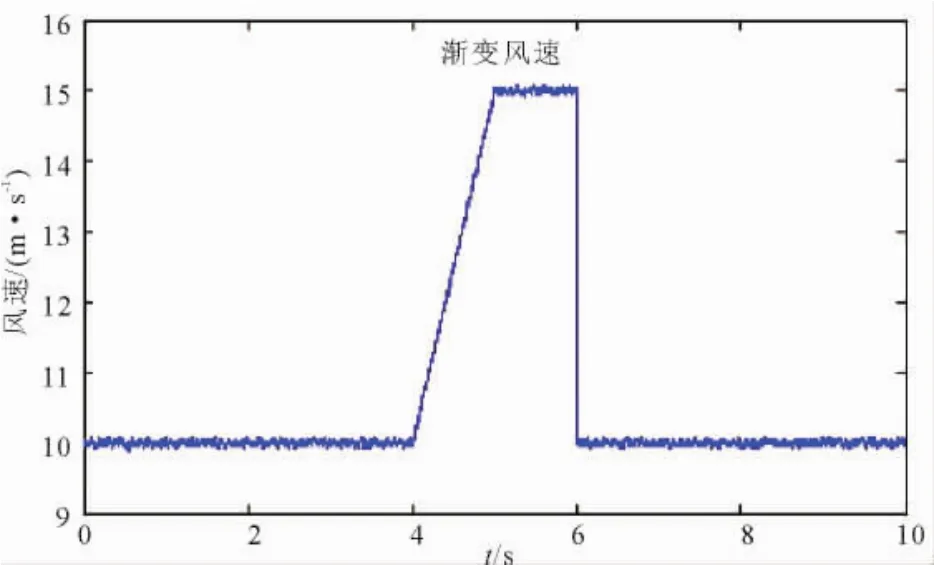
图19 基本风+随机风Fig.19 Basic plus random wind

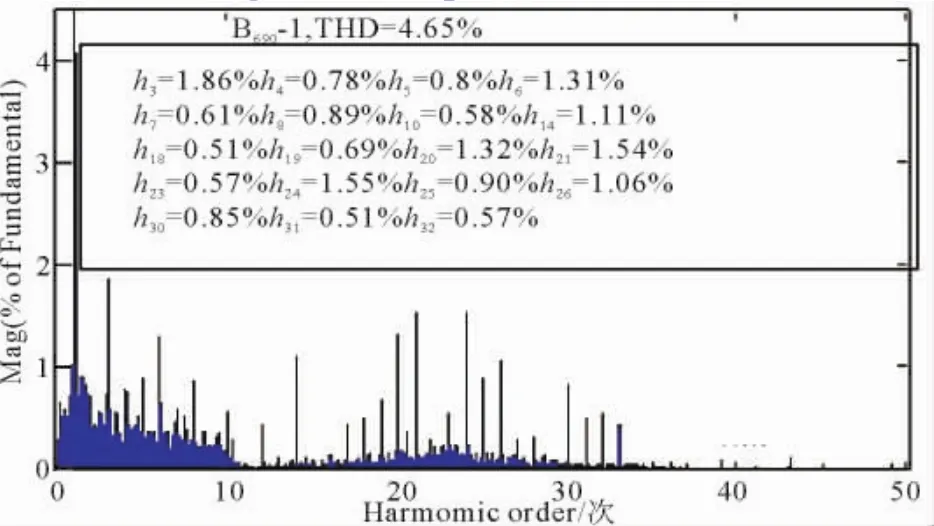
图20 690 V母线电流THDFig.20 The electric current THD of 690 V Bus

图21 690 V母线电压THDFig.21 The voltage THD of 690 V Bus

图22 35 k V母线电压THDFig.22 The voltage THD of 35 kV Bus

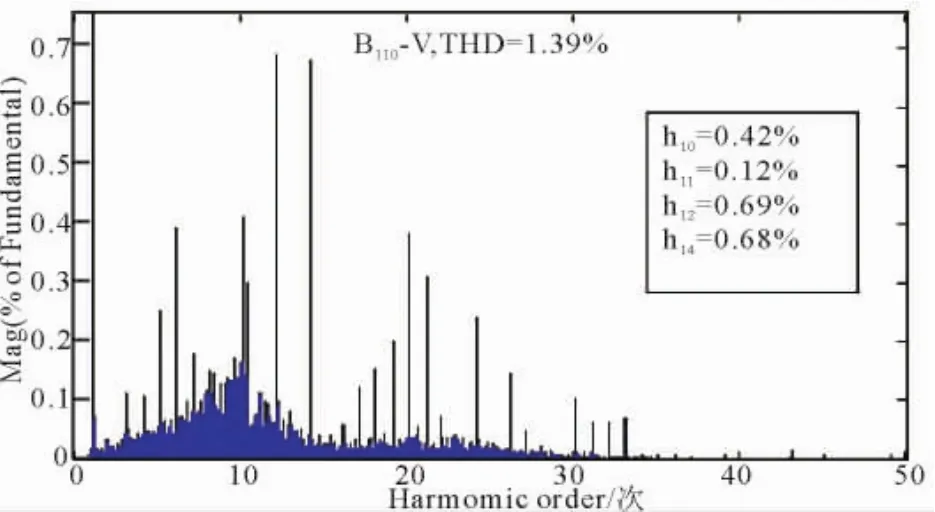
图23 110 kV母线电压THDFig.23 The voltage THD of 110 k V Bus

3.3.4 不同短路容量下谐波仿真分析

仿真条件：设置10 m/s的基本风速作用于风机上，前面已经在40 MVA的容量下得出了其谐波数据，现改变电网短路容量为100 MVA，仿真时间0.2 s，波形如图24—图27所示。

图24 690 V母线电流THDFig.24 The electric current THD of 690 V Bus

图25 690 V母线电压THDFig.25 The voltage THD of 690 V Bus

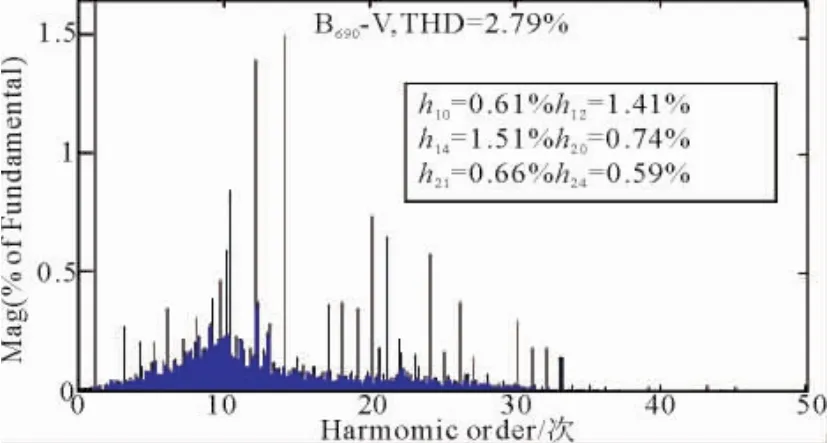
图26 35 kV母线电压THDFig.26 The voltage THD of 35 kV Bus

图27 110 kV母线电压THDFig.27 The voltage THD of 110 kV Bus

4 结语

本文基于MATLAB构建了适合于研究风机并网谐波特性的仿真平台，同时搭建了风速四分量仿真模块，仿真了不同风速和短路容量下，风电场出口母线电压、电流和风机最终并网的110 kV母线的电压、电流的畸变率，得出了风机在不同风速类型作用下的谐波情况。

[1] 郭涛,含双馈风力发电机的风电场谐波分析[D].北京:华北电力大学，2008.

[2] 曹发彦,吴丹岳,陈树棠,等,莆田南日岛风电场电能质量的测试与分析[J].福建电力与电工,2006,26(4):41-44.CAOFa-yang,WUDang-yue,CHENShu-tang,et al.Power Quality Test and Analysis of the Putian Nanri Island Wind Farm[J].Fujian Electric Power and Electrical Engineering.2006.26(4)：41-44.

[3] 黄壮盛.南澳风电场谐波的测量与分析[J].电网技术,2001,25(11):80-82.HUANGZhuang-sheng.The Electric Harmonic Measurement and Analysisof Nan'ao Wind[J].Power System Technology.2001,25(11):80-82.

[4] 张燕涛,黄伦,高红杰，等.电网谐波的危害、监测和治理[J].陕西电力,2007(9):45-48.ZHANGYan-tao,HUANGLun,GAOHong-jie,etal.Harmfulness,Monitoring&Treatment of Network Harmonic[J].System Technology,2007(9):45-48.

[5] 傅旭,李海伟，李冰寒.大规模风电场并网对电网的影响及对策综述[J].陕西电力,2010,23(1):53-58.FU Xu,LI Hai-wei,LI Bin-han.Review on Influences of Large-scale Wind Farms Power Systems and Countermeasures[J].Shanxi Electric Power,2010,23(1):53-58.

[6] 郭相锋,魏鹏飞.浅谈风电场电能质量问题[J].西北水力发电,2007,23(1):23-25.GUO Xiang-feng,WEI Peng-fei.Electric Power Quality of Wind Park[J].Journal of Northwest Hydroelectric Power,2007,23(1):23-25.

[7] 万航羽,黄梅.双馈风力发电机建模与谐波分析[J].电气应用，2008,27(6):53-57.WAN Hang-yu,HUANG Mei.Modeling of Double-Fed Induction Generator and Harmonic Analysis[J].Electrotechnical Application,2008,27(6):53-57.

[8] 黄凯，王斌.风力发电系统中双馈异步发电机的仿真研究[J].计算机仿真,2006,23(7):231-235.HUANG Kai,WANG Bin.Modeling and Simulation of Doubly Fed Induction Machinefor Wind-Energy Generating System[J].Computer Simulation,2006,23(7):231-235.

[9] 李军浩,胡泉伟,吴磊,等.电网谐波对电能计量影响的仿真分析[J].陕西电力，2011(6):01-05.LI Jun-hao,HU Quan-wei,WU Lei.Simulation Study of Harmonic Influence on Electric Energy Metering[J].Shanxi Electric Power,2011(6):01-05.