考虑风电并网的分时段短期电价预测

唐兰兰，温步瀛，江岳文

（福州大学 电气工程与自动化学院，福建 闽侯350108）

在电力市场下，电力作为一种商品，其价格是整个市场的核心，电价的波动影响到各种资源在电力市场中的流动和分配。所以电价预测对于市场中的各个参与者都具有重要意义。然而，由于电价的波动受燃料价格、竞价机组可用容量、水力发电量、输电阻塞等诸多因素的影响，电价表现出较强的波动性和随机性，所以，准确的电价预测也成为电力市场中的研究难点之一。此外，随着可再生能源发电技术的发展和其份额的增加，比如风电，电价曲线的变化较以前更复杂，价格的特性变化更极端，电价预测更困难。

目前短期电价预测有2种方法：时间序列法和基于神经网络的人工智能预测方法。常用的时间序列法有自回归模型和自回归滑动平均模型，通过对历史电价数据的分析建模，文献[1-4]分别采用动态回归模型和自回归滑动平均模型进行短期电价预测。以上的时间序列模型仅从序列自身来寻找电价的变化规律，未充分考虑其他因素对电价的影响，因此存在一定的局限性，预测效果往往不理想。由于神经网络可以有效处理多变量和非线性问题，因此更多的学者则倾向于采用神经网络来预测电价。文献[5]运用人工神经网络对澳大利亚维多利亚州的电价进行了预测研究，文献[6]采用BP神经网络预测短期电价，文献[7-9]分别采用回归神经网络、RBF神经网络和自适应神经网络预测目前市场电价。以上研究均取得了良好效果。

笔者基于对实际短期电力市场电价的分析，主要考虑并网风电量、负荷和历史清算电价对未来时段电价的影响以及神经网络擅长拟合非线性映射这一特点，建立相关的神经网络对电力市场中一星期的清算电价进行预测。同时考虑到不同时间点上电价的不同变化从而将电价序列按照时间点的不同排列为24个电价序列[10]（称为分时段电价序列，如果市场为半小时出清，则有48个电价序列），故笔者对电价序列进行分时段处理，对每一时段电价分别进行预测，以提高预测精度，所建立的电价预测模型是对24个时段分别进行建模预测。算例采用丹麦电力市场中的历史数据，比较了不同输入因素对应于不同神经网络预测方法下的预测精度，以便选取恰当的输入因素对电价进行预测。

1 影响电价的因素

市场环境下影响电价的因素很多，如历史电价、负荷、水力发电量、系统容量、气象等。然而，随着风力发电技术的发展及其份额的增加，电价对于并网风电量的变化非常敏感，任何并网风电量的变化，都会导致电价的上涨或者下跌。因此，并网风电量也成为影响电价的主要因素。

在进行电价预测之前要对各影响因素与电价的相关性进行计算与分析。相关系数可以用来度量各种因素与电价的关联程度，其定义如下：

式中，ρ为相关系数；f为某影响因素，σf为该因素的标准方差；p为电价，σp为电价的标准方差；Cov（f,p）为影响因素f与电价p的协方差。

根据式（1）计算得到丹麦电力市场2009年9月—2010年9月负荷对电价的相关系数（ρ1）、等效负荷对电价的相关系数（ρ2）和并网风电量与负荷的比值对电价的相关系数（ρ3）如表1所示。

表1 不同影响因素与电价的相关系数Tab.1 The correlation coefficient of different affecting factors

从表1可知，各影响因素与电价都具有较强的相关性，其中等效负荷与电价的相关性最大，因为其含有的信息比其他两种影响因素更丰富。此外，历史清算电价也是影响电价的主要因素。

基于以上分析可知，系统的历史清算电价、并网风电量与负荷的比值和负荷是影响电价的主要因素。故分别将负荷与历史清算电价，等效负荷与历史清算电价，负荷、并网风电量与负荷的比值及历史清算电价分别作为神经网络的输入因子对市场清算电价进行分时段预测。

2 基于神经网络的电价预测理论

神经网络[11]是由处理单元组成的一种并行、分布式信息处理结构，处理单元之间由单向信道相互连接。人工神经元是神经网络的基本计算单元，模拟了人脑中神经元的基本特征，一般是多输入/单输出的非线性单元，可以有一定的内部状态和阈值。

2.1 RBF神经网络预测模型

径向基函数网络（RBF）只有一个隐层，隐层单元采用径向基作为其输出特性，输出为隐层的加权求和[12-13]。最常用的径向基函数是高斯函数，形式为：

式中，‖x-m‖为空间任一点x到某一中心m之间的欧式距离；m为核函数中心；σ为函数的宽度参数，控制了函数的径向作用范围。

在RBF网络中m可以通过聚类算法求得，σ可以通过结果和样本的分布计算得到。网络的输出层的训练通常采用递推最小二乘法。

2.2 广义回归神经网络

广义回归神经网络（GRNN）是RBF网络的一种变化形式[14-15]。其理论基础是非线性回归分析，非独立变量y相对于独立变量x的回归分析，实际上是计算具有最大概率值的y。

GRNN是一种基于非线性回归理论的前馈式神经网络，与典型的BP网络不同，它通过激活神经元来逼近函数，也就是实现输入矢量的函数值由某一领域内的神经元矢量对应的函数值映射而逼近。GRNN由输入层、隐含层和输出层组成，结构如图1所示。

隐含层采用高斯变换来控制隐含层输出，从而抑制输出单元的激活。在输入空间，高斯函数对称于接受域。输入神经元对由网络输出的影响随输入矢量之间的距离而呈衰减。

图1 GRNN结构图Fig.1 The structure of GRNN

3 预测评估标准的定义

3.1 传统的评价指标

在预测中，传统的误差评价指标是平均绝对百分比误差（Mean absolute percentage error,MAPE）。设Pi是实际值，而P赞i是预测值，MAPE定义为：

MAPE平均指标被广泛地应用于负荷预测当中，但是在电价预测中，该指标有时不能正确反应预测的好坏。因为电价序列不是一个正值序列，它经常会出现零值和负值。当电价为零值的时候，式（3）就失去了意义，当出现负值时却可能使得误差度量变小，从而导致不合理的结果。

3.2 适用于评价电价的MAPE指标

针对传统MAPE的问题，重新定义MAPE如下：

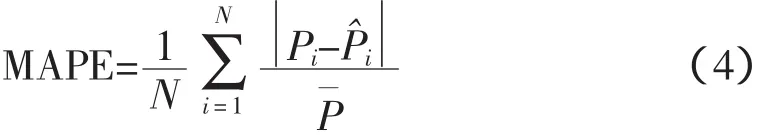
式中，Pi是实际电价；P赞i为预测电价；P軈为N时段实际电价的平均值；N为时段数。

这样重新定义后就不会出现除数为零的情况，从而能够正确地反映预测的效果。因此本文采用式（4）的评价指标。

3.3 概率性评价指标

在电价预测过程中，除了能够利用点对点的绝对误差以及平均百分比误差来评价预测结果以外，还希望能够得到一种概率性指标，通过这种概率性指标来确定预测结果的可信度[13]。基于这种思想利用误差分布函数的概率来确定一种误差评价指标。

选取n个连续样本点的预测误差，把n个预测误差按从小到大的顺序重新排列：{ε（1）,ε（2），…，ε（n）}。那么就定义所选样本预测误差的累积分布函数如下：

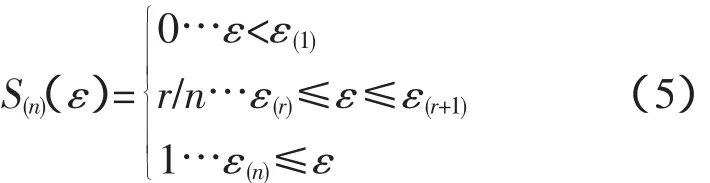
S(n)（ε）就是小于等于的误差值在总样本中的比例，当n选的足够大时，S(n)（ε）就可以很好地拟合误差概率分布函数F（ε）。F（ε＜ε(n)）表征该模型误差小于ε(n)的概率，显然对于指定的ε(n)，F（ε＜ε(n)）越大则预测结果的可信度就越高。故可以把F（ε）作为预测结果的一个有效评价指标。

4 算例分析

4.1 算例1

算例采用丹麦电力市场中的历史数据对其市场出清电价进行短期预测。需要的数据包括历史清算电价、历史负荷和历史并网风电量等。

从丹麦电力市场2010年3月—2010年5月的实际运行数据中筛选54组样本作为训练数据，并对2010年6月6日—2010年6月12日（1星期）的MCP进行预测。其不同输入量对应的预测电价如图2所示，从图2可以看到，3种不同的输入量在电价尖峰时段的预测误差都很大，其中输入量为电价、并网风电量与负荷的比值和负荷（input3）时对应尖峰时段的预测效果要比电价和负荷（input1）与电价和等效负荷（input2）作为输入量时的预测效果好。从图2也可以明显看到，以input3作为神经网络的输入量对6月11日和6月12日进行电价预测所得的预测效果要比另外2种输入量好很多，通过分析各日期的风电出力情况发现6月11日和6月12日不同时段的并网风电量所占的比例几乎都达到了20%，个别时段的并网风电量所占的比例达到40%以上。其他日期的并网风电量所占的比例都在10%左右。2010年6月6日—2010年6月12日预测日中不同输入量的预测误差如表2所示。由表2可以看出，输入量为input2和input3时的预测精度都要比输入量为input1时高，这是因为等效负荷对电价的相关系数要比负荷对电价的相关系数高，input2和input3都考虑了风电的影响故所包含的信息丰富。负荷曲线和等效负荷曲线如图3所示，由图3可知，当并网风电量在电网中所占的比例很小（<10%）时，“等效负荷”的整体变化曲线与负荷变化相似。当并网风电量所占的比例较大（>20%）时，风电的随机波动与负荷的波动叠加在一起，使得“等效负荷”变化剧烈，随着风电入网电量的增加，电价波动性也会增加，所以大规模风电并网后会加大电价预测的难度，观察表2中6月11日和6月12日不同输入量对应预测电价的平均相对误差值可知，当系统中的并网风电量很大时，以等效负荷作为输入量时的电价预测精度不一定比以负荷作为输入量时的预测精度高，因为风电并网后会加大电价的波动从而使电价预测的难度增大。由表2可见，以input3作为输入量所得预测电价的平均相对误差几乎都在10%以下，其预测效果总体上要比其他2种不同输入量所得电价的预测效果好。

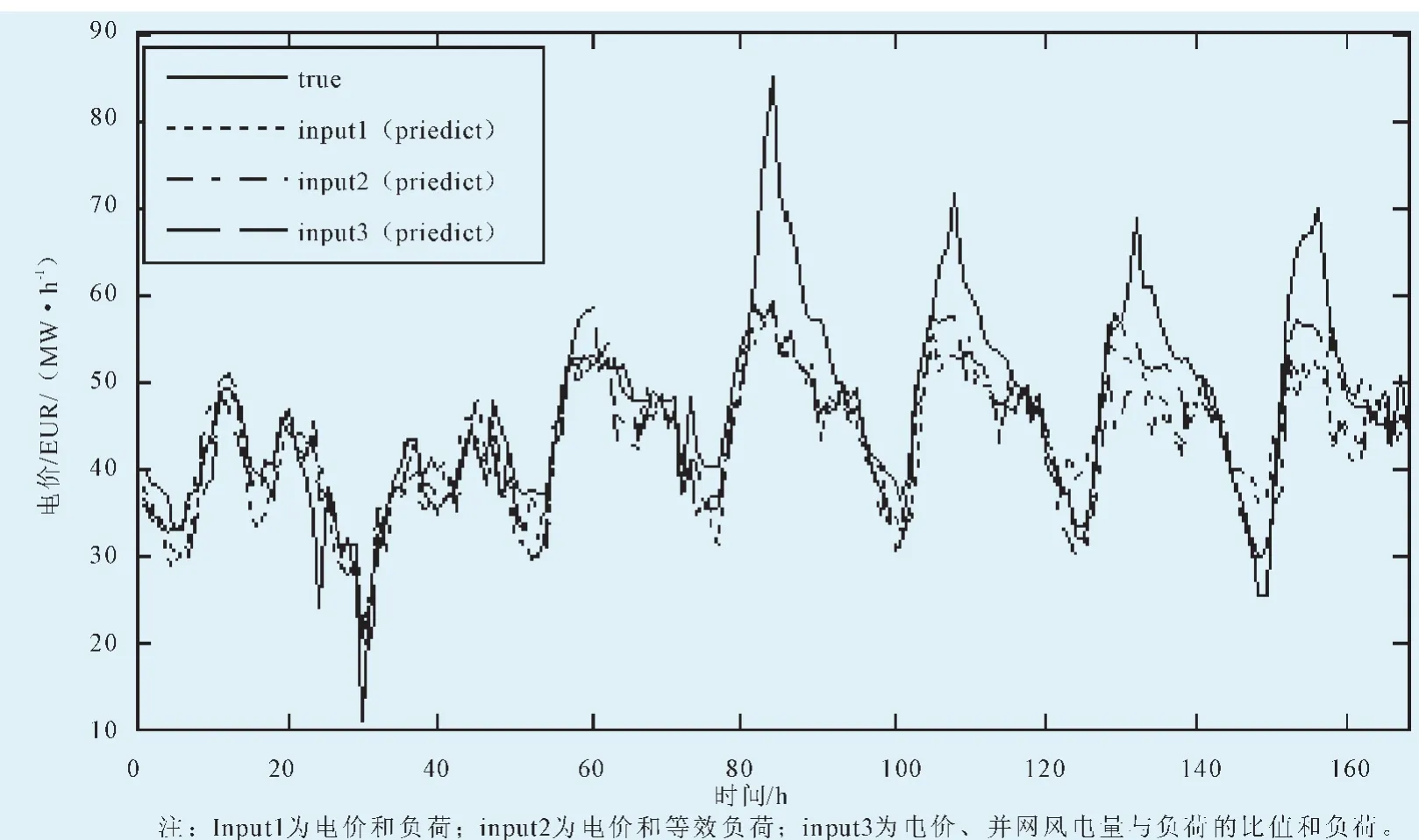
图2 2010年6月6日—2010年6月12日不同输入量对应的RBP神经网络电价预测图Fig.2 Different input of the RBP neural network electricity price forecasting from June 6,2010 to June 12,2010

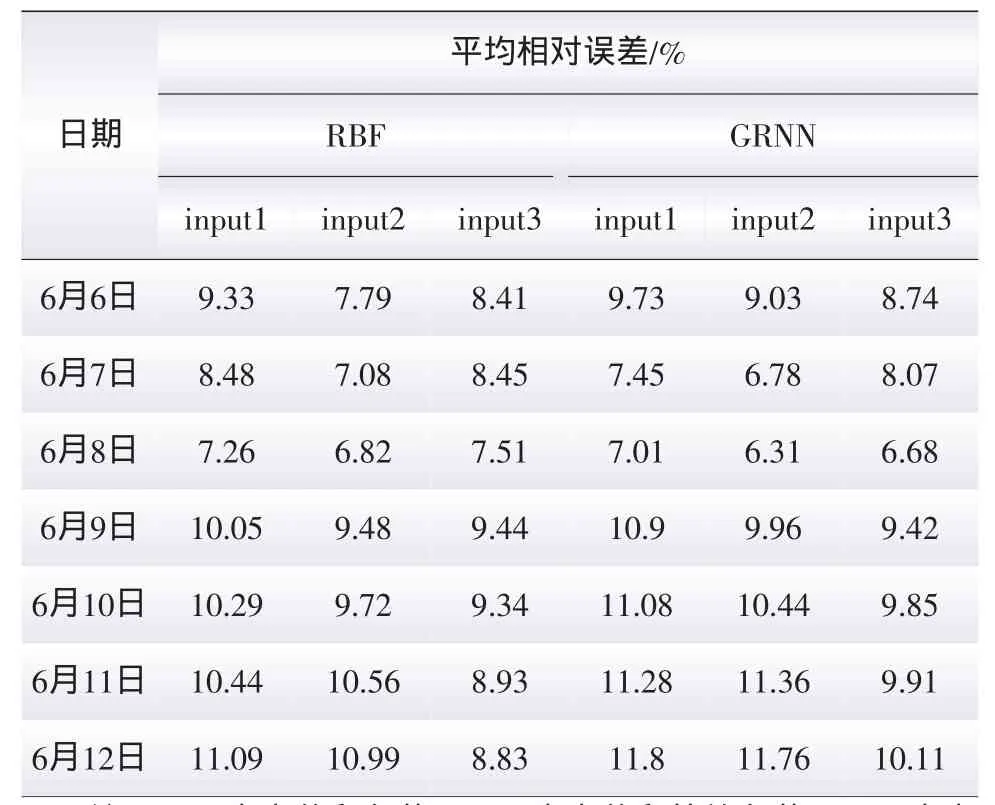
表2 2010年6月6日—2010年6月12日不同输入量预测误差比较表Tab.2 The compare of errors between the different data from June 6,2010 to June 12,2010

图3 实际负荷曲线和等效负荷曲线Fig.3 The actual load curve and equivalent load curve

在分析电价预测的过程中，预测结果的评价指标是一个非常重要的方面。大多数文献的预测工作都是采用平均绝对误差和平均百分比误差等传统误差指标来评估预测结果。但是这些指标都是一种点对点的误差评价标准，不能将预测结果的整体波动性显示出来。我们希望能够得到一种概率性指标，通过这种概率性指标来确定预测结果的可信度，基于这种思想利用误差分布函数的概率来确定一种误差评价指标。

采用丹麦电力市场2010年4—6月的历史清算电价、并网风电量和负荷数据，4—5月的历史数据作为训练数据来预测6月份的电价。根据式（5），利用实际预测结果确定3种不同输入量对应模型的相对误差的概率分布。

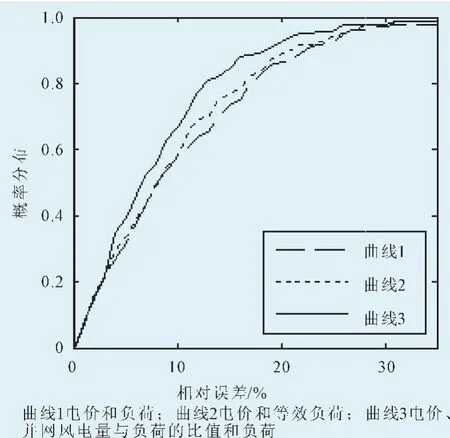
图4 不同输入因子的相对误差概率分布Fig.4 Different input factor of the relative error probability distribution

图4 给出了3种不同输入量对应模型的相对误差的概率分布曲线，由图4可以看出，设定预测的相对误差为10%时，曲线3的概率为66.67%，而曲线1和曲线2的概率分别为57.74%和58.33%。当设定预测的相对误差为15%时，曲线3的概率为84.52%，而曲线1和曲线2的概率分别为73.21%和76.79%。同时还可以看出曲线3的相对误差概率分布曲线整体要高于另外两条曲线，说明曲线3的预测可信度要高于曲线1和曲线2。由此可知电价、并网风电量与负荷的比值和负荷作为神经网络的输入要比另外两种输入量所得预测电价的精度高。

4.2 算例2

为了更好地说明输入量为电价、并网风电量与负荷的比值和负荷（input3）时具有良好的预测效果，故选取并网风电量所占的比例较大的日期作为预测日。从丹麦电力市场2009年10月—2009年12月的实际运行数据中筛选62组样本作为训练数据，并对2010年1月11日—2010年1月17日（1星期）的MCP进行预测。2010年1月11日—2010年1月17日各日并网风电量所占比例的日平均值如表3所示。

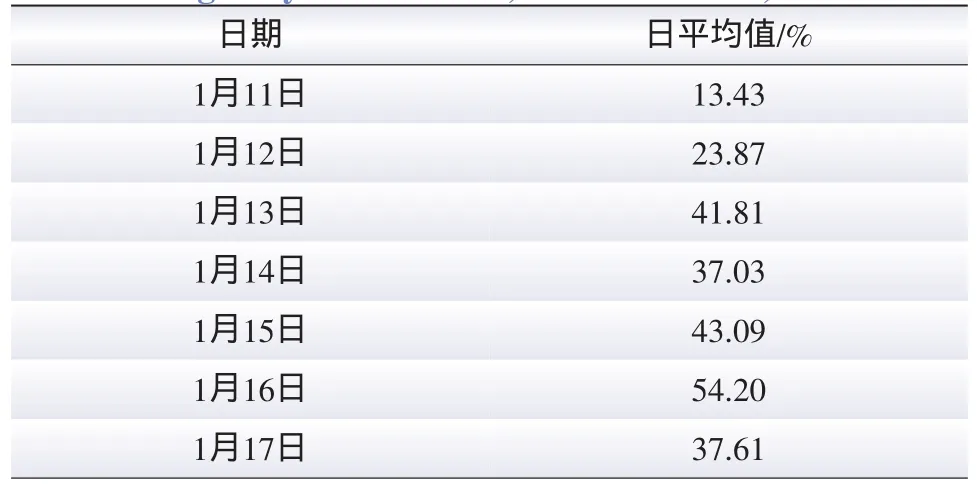
表3 2010年1月11日—2010年1月17日各日并网风电量所占比例的日平均值Tab.3 Power grid wind the percentage of the average day from Jan.11,2010 to Jan.17,2010

2010年1月11日—2010年1月17日中不同输入量对应模型的预测误差如表4所示。

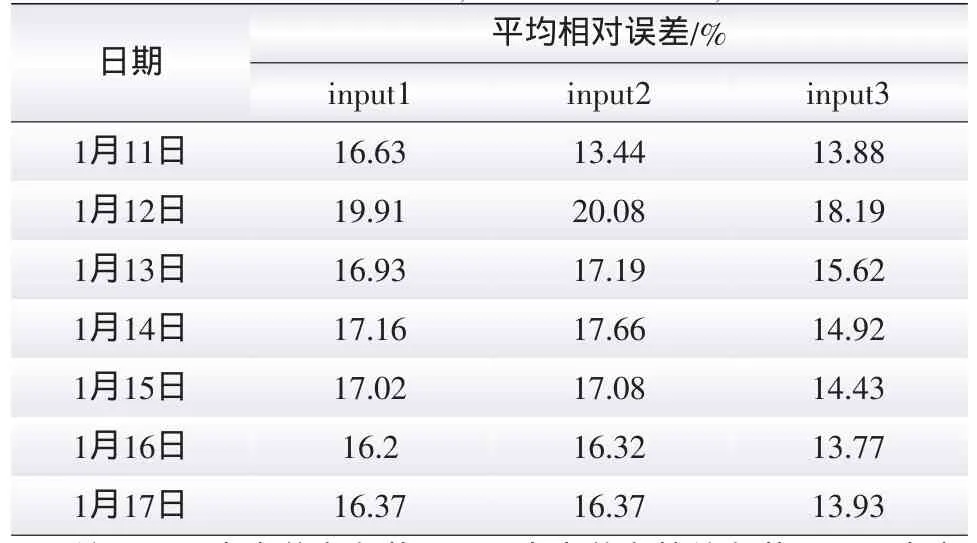
表4 2010年1月11日—2010年1月17日不同输入量预测误差比较表Tab.4 The compare of errors between the different data from Jan.11,2010 to Jan.17,2010

2010年1月11日—2010年1月17日预测日中不同输入量对应模型的相对误差的概率分布曲线如图5所示。

从表4可以看出，以等效负荷作为输入量时的电价预测精度比以负荷作为输入量时的预测精度低，这是因为大规模风电并网后不仅加大了等效负荷的波动同时也加大电价的波动从而使电价预测的难度增大。由表3可知2010年1月11日—2010年1月17日各日的并网风电量所占比例的都很高，最高的比例可达50%以上。由图5可以明显看出曲线3的误差概率分布曲线整体要高于另外2条曲线，进一步说明曲线3的预测可信度要高于曲线1和曲线2。由此可知电价、并网风电量与负荷的比值和负荷作为神经网络的输入要比另外2种输入量所得预测电价的精度高。

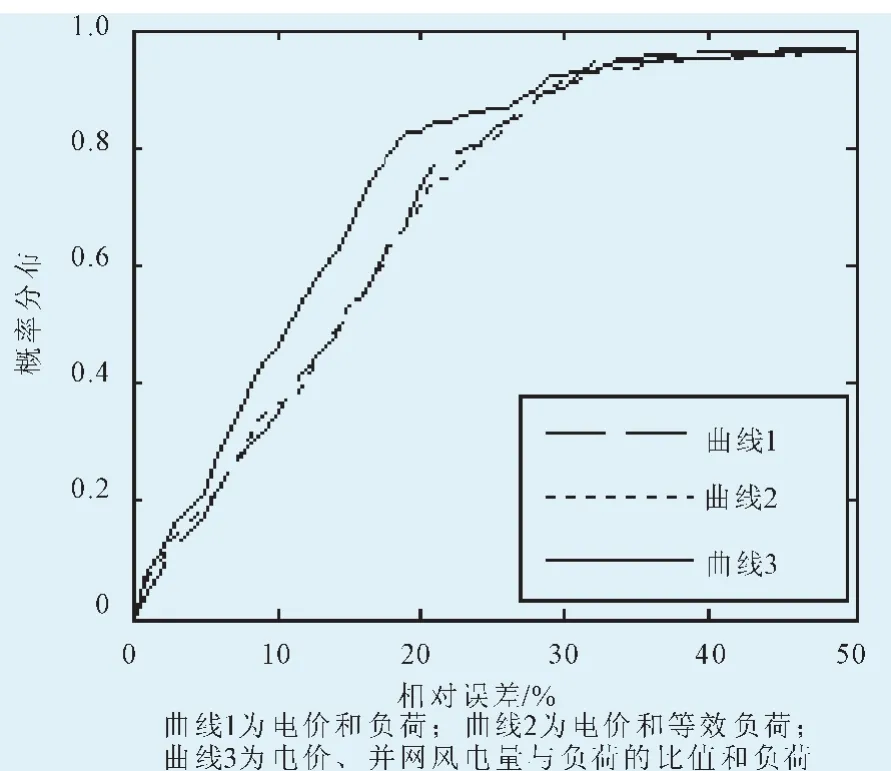
图5 2010年1月11日—2010年1月17日不同输入因子的相对误差概率分布Fig.5 Different input factor of the relative error probability distribution from Jan.11,2010 to Jan.17,2010

5 结语

笔者考虑了并网风电量对电价的影响，并将其视为电价的主要影响因素，将负荷与历史清算电价，等效负荷与历史清算电价，负荷、并网风电量与负荷的比值及历史清算电价分别作为神经网络的输入因子对市场清算电价进行分时段预测。

通过以上分析可以得到以下几点结论。

1）随着可再生能源发电技术的发展和其份额的增加，比如风电，这使得电价曲线的变化较以前更复杂。价格的特性变化更极端，电价预测更困难——部分原因是多种能源的可变性。

2）当并网风电量在电网中所占的比例较小时，以等效负荷作为神经网络的输入量得到的预测效果较好。当并网风电量所占的比例较大时，风电的随机波动与负荷的波动叠加在一起，使得“等效负荷”变化剧烈，同时电价的波动性也会增加，从而加大电价预测的难度。

3）选择电价、并网风电量与负荷的比值及负荷作为预测输入变量是恰当的，电价预测的精度能够满足电力市场实际运行的需要。

本文分时段预测方法尚未考虑到相邻时段电价的相关性，下一阶段的研究重点是在分时段预测方法中引入相邻时段间电价的相关性，进一步提高电价预测的精度。

[1] F RAN CISCOJ．Forecasting Next-day Electricity Prices by Time Series Models[J]．IEEETransaction on Power Systems,2002,17(2):342-348．

[2] 周明,严正.含误差预测校正的ARIMA电价预测新方法[J].中国电机工程学报,2004,24(12):63-68.ZHOU Ming,YAN Zheng.A Novel ARIMA Approach on Electricity Price Forecasting With Improvement of Predicted Error[J].Proceedings of the CSEE,2004,24(12):63-68.

[3] JAVIERContreras,ROSARIOEspinola,FRANCISCOJ,et al．ARIMA Models to Predict Next-day Electricity Prices[J]．IEEETransaction on Power Systems,2003,18(3):1014-1020．

[4] CUARESMA J C,HLOUSKOVA J,KOSSMEIER S,et al．Forecas-ting Electricity Spot-prices Using Linear Univariate Time.

[5] SZKUTA B R,SANABRIA T S,DILLON LA.Electric Price Short-term Forecasting Using Artificial Neural Network Method[J].IEEE Trans.on PWS,1999,14(3):851-857.

[6] GAOFeng,GUANXiao-hong,CAOXi-ren,et al.Forecasting Power Market Clearing Price and Quantity Using a Neural Network Method[A].[sl]:IEEE,2000:2183-2188.

[7] HONGY,HSIAOCY.Locational Marginal Price Forecasting in Deregulated Electricity Markets Using Artificia Lintel-Ligence[J].IEEE Proc.Gener.Transim.Distrib.Sep.2002,149(5):621-626.

[8] GUO Jau-Jia，PETER B Luh．Selecting Input Factors for Clusters of Gaussian Radial Basis Function Networks to Improve Market Clearing Price Prediction[J]．IEEE Trans．Power Syst．Aug．2003,18(3)：665-672.

[9] YAMIN H Y,SHAHIDEHPOUR SM,LI Z．Adaptive Shortterm Electricity Price Forecasting using Artificial Neural Networks in the Restructured Power Markets[J].Electrical Power and Energy Systems,2004,26(8).

[10]张显,王锡凡,陈芳华,等.分时段短期电价预测[J].中国电机工程学报，2005,25(15):1-6.ZHANGXian,WANGXi-fan,CHENFang-hua.Short-term Electriccity Price Forecasting Based on Period-Decoupled Price Sequence[J].Proceeding of the CSEE,2005,25(15):1-6.

[11]曾维欢,魏明海.基于需求预测的陕西电力通信网发展规划研究[J].陕西电力,2010(6).ZENG Wei-huan,WEI Ming-hai.Shaanxi Electric Power Communication Network Development&Plan Based on Demand Prediction[J].Shaanxi Electric Power,2010(6).

[12]谷志红,牛东晓.广义回归神经网络模型在短期电力负荷预测中的应用研究[J].中国电力,2008,39(4):11-14.GU Zhi-hong,NIU Dong-xiao.Research on Application of General Regression Neural Network in Short-term Load Forecasting[J].Electric Power,2008,39(4):11-14.

[13]刘东,李莉.小波神经网络嵌入专家系统的短期电力负荷预测[J].陕西电力,2009,5(10):52-56.LIUDong,LILi.Short-term Power Load Forecasting Based on Wavelet Neural Nentwork Embedding Expert System[J].Shananxi Electric Power,2009,5(10):52-56.

[14]George Chryssolouris,Moshin Lee.Confidence Interval Prediction for Neural Network Models[J].IEEE Trans.On Neural Networks.1996,7(1).

[15]李建兴,王维超.遗传算法在FACTS控制器参数优化中的应用[J].陕西电力,2006(1).LI Jian-xing,WANG Wei-chao.Application of Genetic Algorithm in FACTS Control Parameter Optimization[J].Shaanxi Electric Power,2006(1).

[16]谢培元,游大海.基于遗传算法优化BP网络的提前一天市场清算电价预测[J].电力自动化设备,2004,24(3):53-56.XIE Pei-yuan,YOU Da-hai.Clearing Price Forecast for Day-ahead Market Based on Genetic-Algorithm BP Network[J].Electric Power Automation Equipment,2004,24(3):53-56.

[17] 吴兴华,周晖.基于减法聚类及自适应模糊神经网络的短期电价预测[J].电网技术，2007,31(19):69-73.WU Xing-hua,ZHOU Hui.Short-Term Electricity Price Forecasting Based on Subtractive Clustering and Adaptive Neuro-Fuzzy Inference System[J].Power System Technology,2007,31(19):69-73.