数控凸轮磨床磨削力的模糊适应控制研究

解明利 胡占齐 赵启超 贾 倩

（①燕山大学机械工程学院，河北秦皇岛 066004;②河北石油职业技术学院机械工程系，河北廊坊 065000）

由于凸轮形状的特殊性，通常其磨削余量是不均匀的，而且凸轮磨削工艺系统刚度较差，因此磨削过程中很容易由于磨削余量的不均匀引起磨削力的过大波动，进而引起砂轮的非正常磨损、磨削表面质量变差、甚至工艺系统的损坏。在凸轮磨削过程中引入适应控制技术，保持磨削力的恒定，可以有效地解决这些问题。对于切削适应控制技术，已有较多的文献报道［1－7］，但是用于磨削，特别是凸轮磨削的还很少。本文以笔者开发的数控凸轮磨床为基础，针对凸轮磨削过程的特点，研究了磨削力适应控制系统中的若干关键技术，包括检测参数的选择、磨削进给系统的数学模型、模糊控制器设计等。仿真结果表明，该系统能在磨削余量变化的情况下，保证周向磨削力基本恒定，进而提高凸轮磨削表面质量。

1 凸轮磨削工艺系统的数学模型

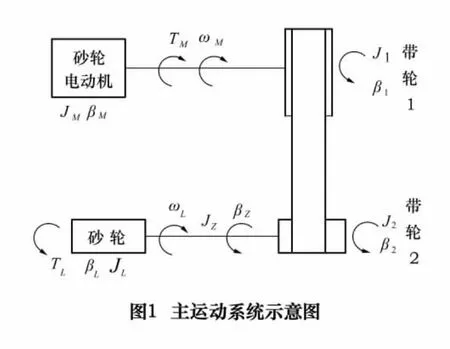
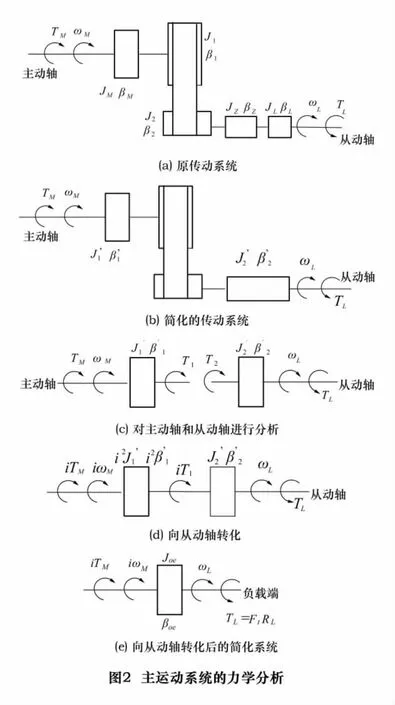
砂轮架是数控凸轮磨床磨削系统的重要部分，它上面的交流电动机通过带传动为砂轮磨削提供动力。磨床主运动系统可以简化成如图1所示的结构。对其进行力学分析，如图2a所示。其中JM为交流电动机的转动惯量，JL为砂轮的转动惯量，J1为带轮1的转动惯量，J2为带轮2的转动惯量，JZ为磨头的转动惯量;TM为交流电动机的输出转矩，TL为负载力矩;ωM为交流电动机和带轮1的转速，ωL为带轮2和砂轮的转速;β1为带轮1处的阻尼，βM为电动机的阻尼;β2为带轮2处的阻尼，βZ为磨头的阻尼。分别对主动轴上的转动惯量和阻尼进行合并，再对从动轴上的转动惯量和阻尼进行合并，可以得到图2b。其中:

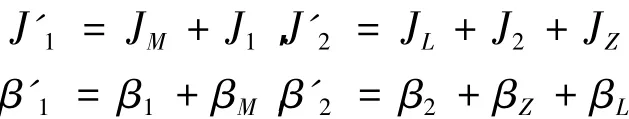
对图2c分析，主动轴和从动轴旋转运动方程如式（1）和（2）。

其中:T1为主动轴大带轮端力矩;T2为从动轴小带轮端力矩;ω'M、ω'L分别为主从动轴的角加速度。

由平衡方程得

将式（1）和式（2）联立，依图2d列得平衡方程

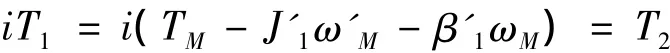
即

通过以上推导，建立了负载力矩与带动砂轮转动的电动机的输出转矩之间的关系，经过进一步的简化，得到图2e。从而得出磨削力的关系式，即

其中:TL=Ft·RL，RL为砂轮的半径，Joe、βoe分别为折合到从动轴的等效转动惯量、阻尼系数。

本文的数控凸轮磨床主电动机采用交流异步电动机，型号为Y－112M。具体参数［8］如表1所示。

表1 Y－112M型电动机参数

此交流电动机的矩频特性曲线如3所示。

在ωm到ω0的转速范围内，当负载增大/减小时，随着转速下降/上升，电动机的转矩增大/减小，直至与负载平衡。该区为稳定区。磨床实际工作要求交流电动机一般要工作在稳定区域。所以可把图3线性化，得到图4。在该线性化过程中，为了减小倾角α的误差，在计算时取原曲线上的点（TN，ωN）和（Tm，ωm）这些点分别与点（0，ω0）连接，然后计算各自的倾角。

取平均值

得到倾角α的值约为9．25°。

从图4可得出转矩与转速之间的关系式为

将式（6）代入式（4）得

其中ωm=iωL;最后整理得

通过分析式（7）发现，一旦交流电动机的型号确定，式（7）中只有ωL和ω'L未知，这就使得要想得到最后磨削力的大小，必须想办法得到ωL和ω'L，它们分别代表了砂轮的角速度和角加速度，是一个比较容易在实际加工过程中测得到的物理量。

反过来，如果知道了磨削力值的大小，就可以知道在稳定状态下的砂轮转速的大小。因此，根据实际加工时的经验确定合理的磨削力值后，就可计算出对应的砂轮转速。这样，对于磨削力的控制就可以从直接对磨削力控制转换为对砂轮转速的控制。而目前有经验的操作者大多正是根据加工时砂轮转速的变化去控制磨削力的大小。

2 模糊控制器设计

2．1 模糊控制器输入、输出变量的选择

由于模糊控制规则是根据人的手动规则提出来的，所以输入、输出变量要与人的手动控制过程中的输入、输出变量保持一致。在凸轮磨削的磨削力的手动控制过程中，操作者的方法是通过观察砂轮转速，来调节系统砂轮进给速度倍率滑块对磨削力给予控制。依此可以确定二维模糊控制器的输入变量为砂轮转速（前文已建立了砂轮转速与磨削力之间的关系式，所以通过计算可将砂轮转速转换为磨削力）和砂轮转速的变化率，输出变量为进给速度倍率k（控制量）。

2．2 模糊控制器输入变量、输出变量论域和模糊集的确定

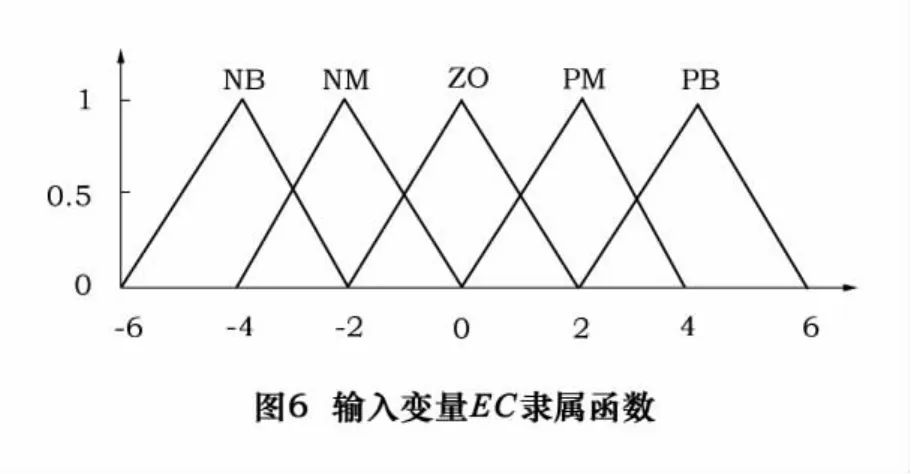
根据平时的加工经验对砂轮转速的偏差E用7个词汇进行描述{负大NB、负中NM、负小NS、零Z、正小PS、正中PM、正大PB}，砂轮转速偏差的变化率EC用5个词进行描绘{负大NB、负中NM、零Z、正中PM、正大PB};控制量U的描绘用6个词进行描绘{负大NB、负中 NM、负小 NS、零 Z、正小 PS、正大 PB}。在模糊控制器中，基本论域的变量要变换到内部论域的变量，分别用e*和ec*表示。根据实际工况，得到砂轮转速偏差e及偏差变化ec的基本论域为［－10，10］和［－1 000，1 000］。设偏差变量e的基本论域变换到模糊子集的论域为{－6，－5，…，0，…5，6}，偏差变化ec的基本论域变换到模糊子集的论域为{－6，－5，…，0，…，5，6}。

量化因子Ke和Kec决定了模糊控制器对输入误差e及误差变化率ec的灵敏度，Ke和Kec由e/E和ec/EC来确定，Ke和Kec分别取为0.6和0.006。

2．3 模糊控制器的隶属度函数的确定

模糊变量的隶属度函数反映的是该模糊变量模糊子集的定义，相应的可以用不同的隶属度函数曲线来表示，一般曲线类型有三角形、钟形、高斯函数型等。其中，隶属度函数曲线形状较尖的模糊子集，其分辨率较高、控制灵敏度也较高。相反，隶属度函数形状较缓、控制特性也较缓，系统稳定性好。本文选用三角形隶属函数作为输入、输出模糊变量的隶属函数。如图5～7所示。在k时刻输入信号的值ek和eck，经论域变换后得到和，再根据隶属函数的定义可以分别求出和对各模糊集合的隶属度，这样就把普通变量变成了模糊变量，完成了模糊化工作。

2．4 模糊控制规则库的设计

模糊控制器的模糊控制规则采用Mamdani推理法。Mamdani推理法是一种在模糊控制中普遍使用的方法，它本质上仍然是一种合成推理方法。该控制器的模糊规则是人们通过学习、实验以及长期经验积累而逐渐形成的，存储在操作者头脑中的一种技术知识集合。手动控制过程一般是通过对凸轮磨削过程的观测，操作者根据已有的经验和技术知识，进行综合分析并做出控制决策，使凸轮磨削过程中凸轮磨削力得到有效的控制。现将操作者在操作过程中要遇到的各种可能出现的情况和相应的控制规则汇总，见表2。规则采用如下形式

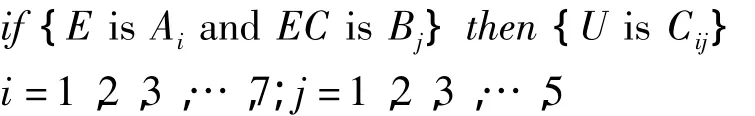
其中，Ai、Bj、Cij是定义在误差e、误差变化率ec和u论域上的模糊集。

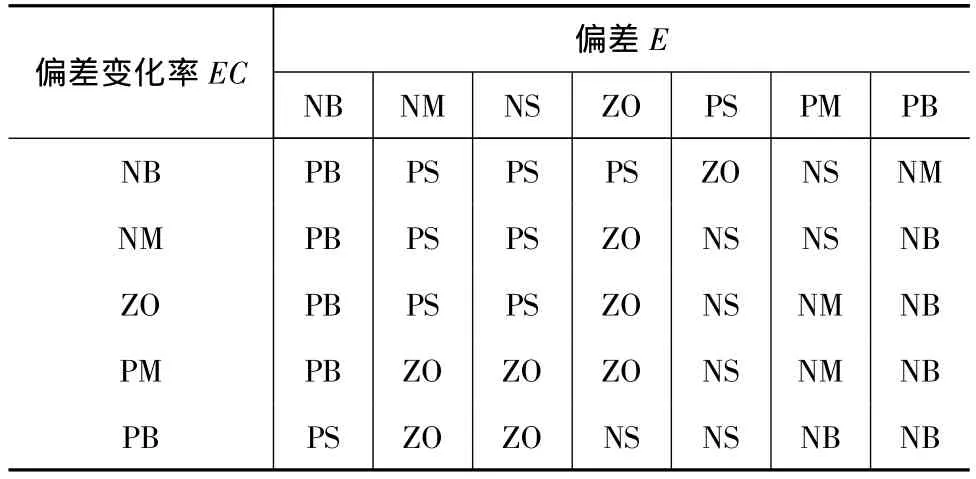
表2 模糊控制规则

2．5 模糊量的清晰化

模糊量的清晰化过程目的是求得最终的控制参数U值。模糊量的清晰化常用的方法有最大隶属度法、重心法、二等分法和中间最大值法等。本文在模糊控制器的解模糊过程中采用二等分法。

每次采样经模糊控制算法给出的控制量，还不能直接控制对象，而必须将其转换到被控制对象所能接受的基本论域中去。输出量的比例因子由式（8）确定，即

其中:yu=1．2为控制量即进给速度倍率的基本论域的最大值，l=12为控制量即进给速度倍率的论域的最大值。由式（8）得Ku=0.1。

3 系统仿真

本文以数控凸轮磨床磨削过程为研究对象，其相关参数如下:选取已有的凸轮磨床磨削轴承钢凸轮的数控加工程序。程序中的虚拟合成速度值为12，得到工件线速度为Vw≈0.012 6 mm/min，磨削深度ap=0.03 mm，工件的轴向宽度为b=20 mm，根据实际操作经验，凸轮磨削过程磨削力的范围在150～200 N，取180 N对应的砂轮转速531 rad/s作为控制系统的参考值。

通过Matlab/Simulink对建立的模糊控制系统进行仿真分析，模拟控制系统的设计流程如图8所示。由于在模拟磨削控制过程中，Simulink模块无法提供砂轮转速信号，因此，F0模块的作用在于依据式（7）计算出由于磨削深度的变化而导致的实际砂轮角速度是多少，这样就可以产生出一个砂轮转速的信号，并与设定值进行比较，产生偏差后，模糊控制器便可以进行调节控制了。

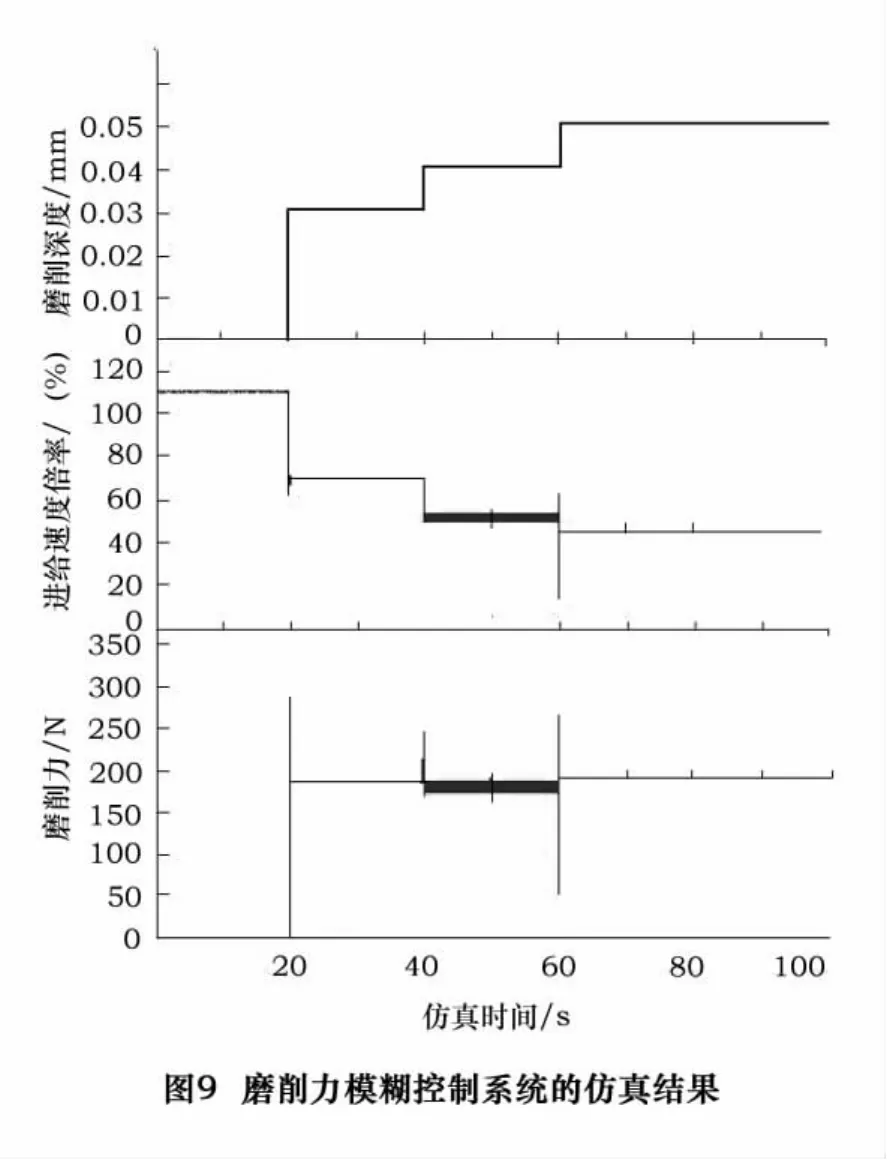
仿真时设定正常凸轮磨削深度为0.03 mm，随着实际的切削变化，从加工切削时间在40 s后，每隔20 s发生一次阶越变化，如图9所示。模糊控制系统按模糊推理合成规则计算出进给速度调整倍率，从仿真曲线可以看出，经过控制系统的调整，在整个凸轮磨削的过程中，磨削力基本控制在180 N，达到了控制系统的预期目的。

4 结语

（1）通过对数控凸轮磨床主传动系统进行分析，建立了该凸轮磨床磨削过程的磨削力数学模型，并在其基础上，对电动机矩频特性做了线性化处理，得到了磨削力与砂轮转速的关系，从而设计出磨削力的间接检测和控制方法。

（2）采用模糊控制系统，根据反馈的砂轮转速，由模糊控制器计算出砂轮进给速度倍率对转速实时修正，实现对数控凸轮磨床磨削力的控制。

（3）通过仿真分析，采用模糊控制策略的数控凸轮磨床磨削系统，在磨削深度发生变化而引起磨削力波动时，经过控制系统调整，磨削力稳定在设定值、提高了凸轮磨削质量。仿真结果表明，采用模糊控制策略的凸轮磨削过程，将使整个磨削过程具有很强的处理未知非线性被控对象的能力，而且控制性能良好，自适应能力强。

［1］程涛，左力，杨叔子，等．数控机床切削加工过程智能自适应控制研究［J］．中国机械工程，1999，10（1）:26 －31．

［2］赖兴余，叶邦彦，鄢春艳，等．基于现场总线的铣削加工过程自适应模糊控制［J］．华南理工大学学报:自然科学版，2005，33（5）:7－10．

［3］冯小军，朱华双，宁仲良．数控铣削模糊自适应控制系统［J］．组合机床与自动化加工技术，2004（7）:73－76．

［4］Yau Hong T，Tsou Lee S，Tong Yu C．Adaptive NC simulation for multi－ axis solid machining［J］．Computer－ Aided Design and Applications，2005，2（1）:95－104．

［5］Zhang Julie Z，Chen Joseph C．The development of an in－process surface roughness adaptive control system in end milling operations［J］．International Journal of Advanced Manufacturing Technology，2007，31（9）:877－887．

［6］Chen Xisong，Li Shihua，Zhai Junyong．Expert system based adaptive dynamic matrix control for ball mill grinding circuit［J］．Expert Systems with Applications，2009，36（1）:716 －723．

［7］Zuperl U，Cus F，Reibenschuh M．Neural control strategy of constant cutting force system in end milling［J］．Robotics and Computer－ Integrated Manufacturing，2011，27（3）:485－493．

［8］机械工程师手册编辑委员会．机械工程师手册［M］．北京:机械工业出版社，2000．