粒子滤波在MEMS陀螺仪初始对准中的应用*

崔 铭

(中国民航大学智能信号与图像处理天津市重点实验室，天津 300300)

MEMS(Micro-Electro-Mechanical-Systems)即微机械电子系统［1－3］，该技术出现于20世纪80年代中后期，是随着现代微电子与微加工工艺的迅速发展而发展起来的，并受到各国家广泛的重视。MEMS-IMU(微机电惯性测量单元)主要包括陀螺仪和加速度计，由于体积小、成本低、重量轻和可靠性高等优点，在低成本惯导系统中广泛应用。但由于理论和制造工艺的不完善，MEMS IMU本身存在着较大的测量误差，其测量值包含许多因素引起的误差，需对这些误差进行测试和建模补偿。误差通常分为确定和随机两部分，确定部分可以用代数方程来表示，具有规律性容易补偿。目前，国内外对这两种误差的补偿已经非常成熟。而随机部分具有不确定性，只能用统计规律来描述，通过滤波的方法来减少。

因而，对陀螺仪输出数据建模后，常采用卡尔曼滤波技术［4－5］。卡尔曼滤波是一种实用的线性最小方差估计算法，适用于非平稳过程，并与递推最小二乘估计一样，算法采用递推，从量测信息中提取被估计量存在估计值中。理想情况下，卡尔曼滤波能得到较好的滤波效果，但在强非线性和非高斯环境下采用卡尔曼滤波会带来较大误差，跟踪性能较差，甚至会出现滤波发散。

粒子滤波［6－9］是一种基于贝叶斯估计的滤波方法。其基本思想:首先依据系统状态向量的经验条件分布，在状态空间产生一组随机样本，这些样本称为粒子，然后根据观测量，不断地调整粒子的权重和位置，通过调整后的粒子的信息，修正最初的经验条件分布。当粒子数目足够多时，修正后的经验条件分布将收敛于系统状态向量真实的条件分布。此时，状态向量的估计值可以通过粒子的均值得到。这种滤波算法采用递推方式，很方便用计算机实现，并且该算法能较好地适应观测信息出现异常突变时的情况，具有一定的鲁棒性，优于标准卡尔曼滤波算法。文章较详细地对粒子滤波进行分析，给出MEMS陀螺仪数据处理中粒子滤波具体模型和滤波算法，最后给出应用分析。

1 粒子滤波

1.1 粒子滤波基本理论

粒子滤波算法［10］是一种随机抽样方法，它的抽样计划不是始终保持不变，而是根据实际结果不断进行调整，设计出新的抽样计划。从所有测量值集合Y1:k={Yi，i=1，2，…，k}中对状态Xk进行估计，即需要构造后验密度P(Xk|Y1:k)，由贝叶斯推论可以得到后验密度的递归形式，分为预测

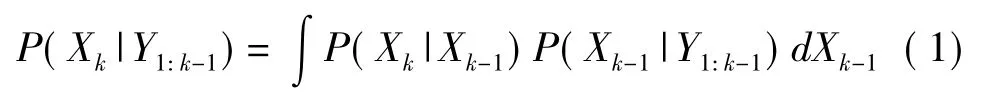
和更新

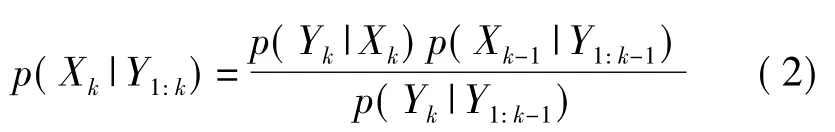
两部分。

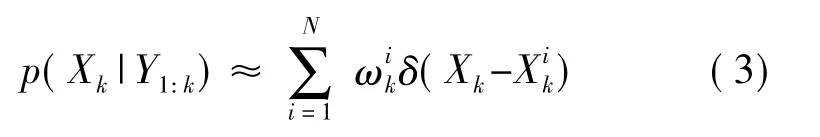
其中Xk表示状态向量，δ()为冲激函数。则k时刻位置和速度的MMSE(最小均方误差)估计可以近似为

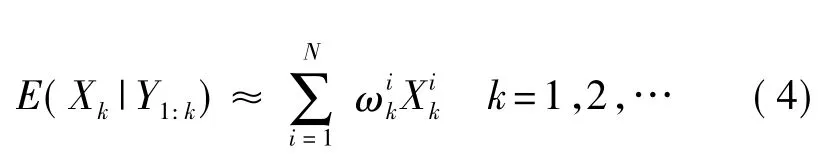
根据重要度抽样选择权重，

根据状态模型知

式中为Qk－1系统噪声的协方差矩阵。

粒子滤波算法在几次迭代之后，会出现退化问题，即归一化权值会集中在一个粒子上面，而其他粒子的权值小到可以忽略的程度。J.Liu提出了用有效抽样Neff来度量退化的程度［11］

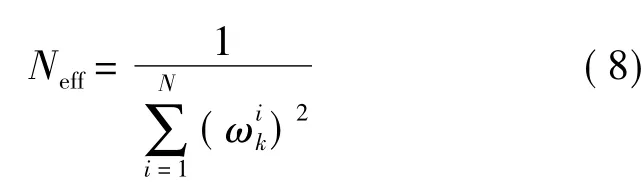
Neff越小表明退化现象越严重。当Neff低于某个门限(比如2N/3)时，就要进行再抽样。再抽样的思想是消除小粒子，复制大粒子。所以我们选择先验分布服从正态分布p(X0)～N(u，δ2)，均值u为利用第一个抽样点的测量信息用几何交点法得到的结果，方差δ2为一个较大的数。相对于无信息先验分布，这种选取方法利用了先验信息，能够使初始分布较接近真实分布，使得粒子集中在后验分布附近。

1.2 算法描述流程图

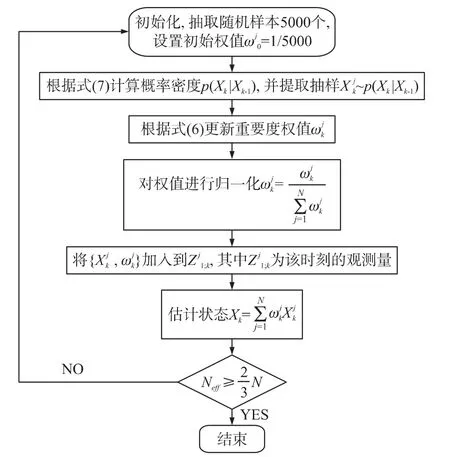
2 系统状态方程的建立

本文采用机动目标Singer模型［12］来描述系统状态，相关理论在参考文献［12］中有详细的论述。设采样周期为T，通过典型的离散处理方法，我们可以得到Singer模型的离散状态方程:

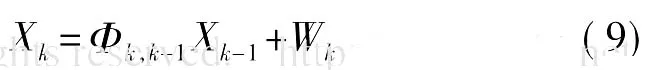
其中

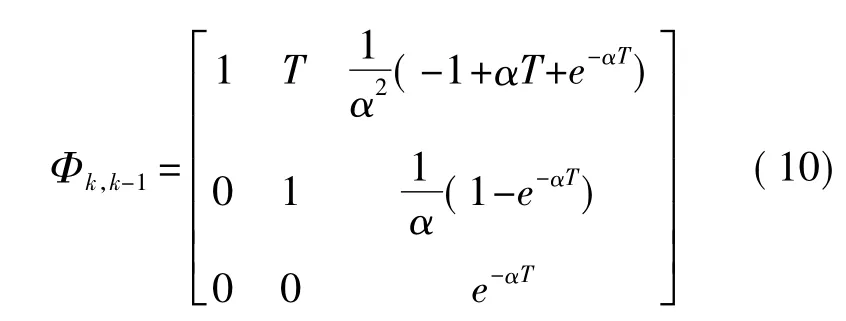
式中Wk是离散时间白噪声序列，并且

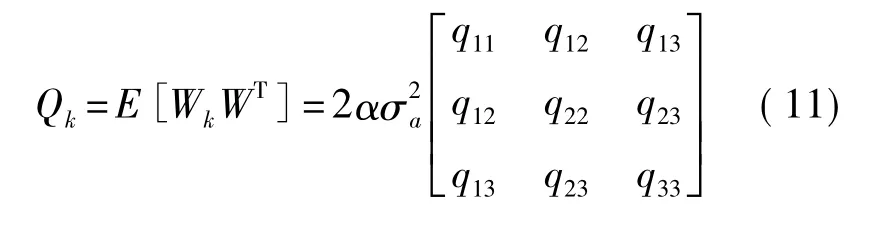
其中

观测方程为

其中当仅有含噪声的目标位置数据可观测时，有Hk=［1 0 0］。Vk是均值为零，方差为Rk的高斯观测噪声。

Singer模型量测量通常是机动目标的位置，滤波估计量是目标的位置、速度和加速度。当把Singer模型用于对MEMS陀螺仪输出数据的滤波时，量测量则是运动角速率，滤波估计量也是运动角速率。因为在对MEMS陀螺仪输出数据的滤波过程中对角速率积分的结果角度值进行估计没有意义，所以可将三维状态方程简化为只有角速率和角加速度的二维状态方程，量测方程的量测矩阵由Hk=［1 0 0］变为 Hk=［1 0］。维数的降低必然会使计算量、计算时间减少，更适于实时滤波需要。

3 应用实例及结果分析

为了比较标准卡尔曼滤波和粒子滤波的滤波效果，我们分别用标准卡尔曼滤波算法和粒子滤波算法对MEMS陀螺仪输出的数据进行滤波处理。

图1所示是一组实测的GPS/SINS组合导航系统处于初始对准状态时X轴MEMS陀螺仪输出的5 000点数据，采样频率为100 Hz。

对MEMS陀螺仪输出数据进行滤波前的预处理的，提取出随机常数和趋势项后数据如图2所示。

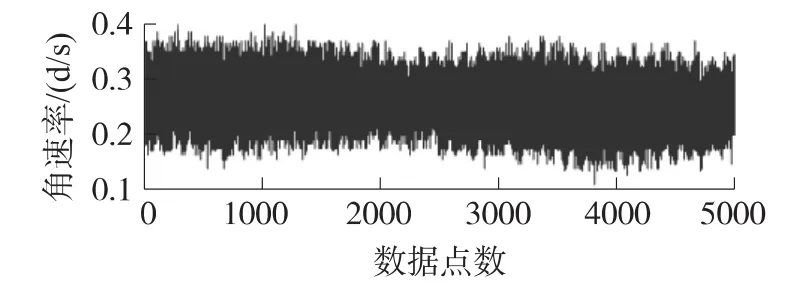
图1 陀螺X轴初始对准状态输出数据

图2 提取出随机常数和趋势项后陀螺X轴数据

经统计分析发现，在SINS进行初始对准时，陀螺仪输出的数据是在常数的基础上叠加了噪声成分。在这种情况下，机动频率是很小的正数，角加速度绝对值的最大值也不会很大。基于这样的事实，设定机动频率 α=0.001，最大正角加速度可设为1.5 d/s2，绝对值最大的负角加速度可设为－1.5 d/s2。

3.1 用标准卡尔曼滤波对输出数据的滤波实现

将图2所示数据直接运用标准卡尔曼滤波算法进行滤波，效果如图3所示。

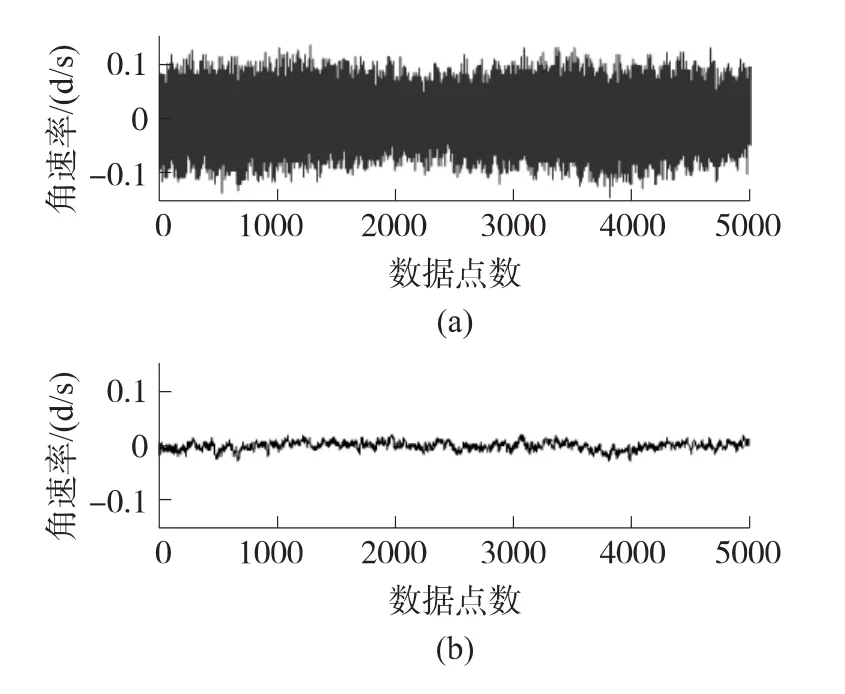
图3 卡尔曼滤波前与滤波后的数据

3.2 用粒子滤波对输出数据的滤波实现

将图2所示数据直接运用粒子滤波算法进行滤波，效果如图4所示。

本文选取MEMS陀螺仪初始对准状态时X轴的输出数据，进行经典卡尔曼滤波与粒子滤波对比实验。从图3和图4的滤波结果可直观的看出，经典卡尔曼滤波算法和粒子滤波算法都能较好完成滤波任务。进一步对两种算法滤波前后的数据进行计算分析，如表1所示，由于两种算法应用同一组MEMS陀螺仪输出数据，故对两种滤波前后的方差和均值进行对比，发现两种算法所得均值相差不大，方差比滤波前减小两个数量级，而粒子滤波的性能要稍好。

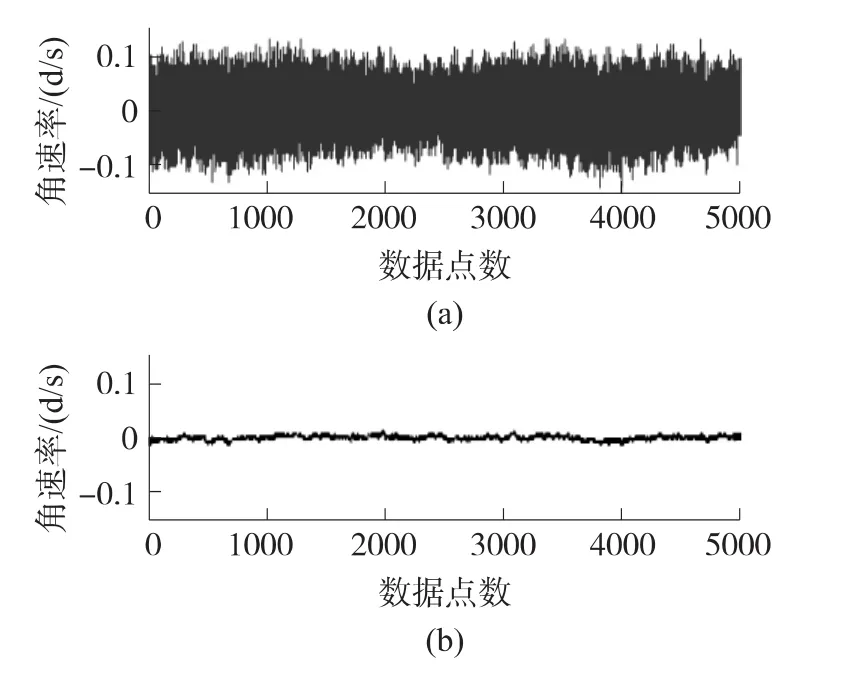
图4 粒子滤波前与滤波后的数据

表1 卡尔曼滤波与粒子滤波前后的均值与方差对比

3.3 用粒子滤波对动态数据的滤波实现

当机体处于运动状态时，角加速度的绝对值的最大值通常是比较大的正数。为了研究粒子滤波性能，对图5所示的实测MEMS陀螺仪输出的典型动态数据进行滤波。

图5 实测MEMS陀螺仪输出的典型动态数据

根据实际中机体的角运动情况，机动状态时，机动频率相对于机体静止时的机动频率要大一些，考虑到这些因素的影响，设定机动频率α=0.01，正负最大角加速度分别设定为10 d/s2和－10 d/s2。根据这些设定，粒子滤波效果的局部放大图如图6所示。

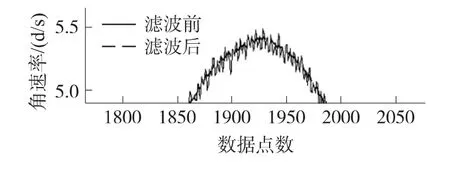
图6 粒子滤波效果局部放大图

从图6可以看出，采用粒子滤波算法对MEMS陀螺仪输出的动态数据进行滤波，可以获得较为理想的滤波效果。应该注意的是，实际中加速度绝对值的最大值通常是未知的，机动频率通常也难以准确确定，这就需要根据机体的具体运动情况根据经验进行确定，从而制约该算法的通用性。但如果我们能够对某种机动的最大加速度和机动频率有适当的了解，运用Singer模型和粒子滤波算法能够获得比较理想的滤波效果。

4 结论

粒子滤波和卡尔曼滤波是两种重要的数据处理方法。本文中，首先采用粒子滤波和卡尔曼滤波分别对静态数据进行处理，粒子滤波后得到效果比卡尔曼滤波稍好。而当机体处于运动状态时，角加速度的绝对值是比较大的正数时，采用粒子滤波算法的同样得到比较理想的滤波效果。但该算法也有其局限性，在实际当中的应用效果将在日后做进一步研究。

［1］祝燕华，蔡体菁，杨卓鹏.MEMS-IMU/GPS组合导航系统的实现［J］.中国惯性技术学报，2009，17(5):552－556.

［2］吉训生，王寿荣.硅微陀螺漂移数据滤波方法研究［J］.传感技术学报，2008，21(2):333－336.

［3］李杰，张文栋，刘俊.基于时间序列分析的Kalman滤波方法在MEMS陀螺仪随机漂移误差补偿中的应用研究［J］.传感技术学报，2006，19(5):2215－2219.

［4］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998，1－5.

［5］付梦印，邓志红，张继伟.kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003，65－104.

［6］田世君，陈俊，皮亦鸣.粒子滤波在高动态GPS定位中的应用［J］.测绘学报，2007，36(3):274－278.

［7］Pau Closasy，Carles Fern’andez-Prades，Juan A Fern’andez-Rubio.A Particle Filtering Tracking Algorithm for GNSS Synchronization Using Laplace’s Method［C］//IEEE International Conference on Acoustics，Speech and Signal Processing，2008:3409－3412.

［8］Javad Rezaie，Behzad Moshiri，Araabi Babak N，et al.GPS/INS Integration Using Nonlinear Blending Filters［C］//Annual Conference on SICE，2007:1674－1680.

［9］Wang Fasheng，Lin Yuejin.Improving Particle Filter with A New Sampling Strategy［C］//Nanning，China:4th International Conference on Computer Science ＆ Education，2009:408－412.

［10］程水英，张剑云.粒子滤波评述［J］.宇航学报，2008，29(4):1099－1109.

［11］LIU V J，COLAJANNI.Dynamic Load Balancing on Web-server System［J］.IEEE Internet Computing，1999，3(3):28－39.

［12］周宏仁，敬忠良，王培德.机动目标跟踪［M］.北京:国防工业出版社，1991，109－153.