一种新型谐波传动试验台的研制
2011-10-18余新木梅雪松王宋萍
余新木 梅雪松② 陶 涛 赵 飞 聂 彤 王宋萍
(①西安交通大学机械工程学院,陕西西安710049;
②西安交通大学机械制造系统工程国家重点实验室,陕西西安710039)
1955年,C.W.Musser创造性地提出了谐波传动技术[1]。这种传动技术采用独特的柔性机构实现动力传递,具有传动比大、精度高、体积小、承载能力大以及可向密闭空间传递运动等性能优势,因此日益受到工程界的重视。自1962年NASA首次将谐波传动应用于Telstar通讯卫星以来,谐波传动已在太阳翼驱动机构、天线指向机构、扫描机构、着陆器行进轮、自动武器制导、机械臂等空间机构中得到广泛应用[2-3]。
谐波传动系统特性的研究一直受到关注。麻省理工学院T.D.Tuttle等研究了谐波传动的非线性动力学特性,构建了由编码器、电动机、扭矩传感器、惯性负载和旋转变压器等组成的试验装置[4]。蒙特利尔麦吉尔大学H.D.Taghirad等对谐波传动在引入摩擦与变形等因素时的动态性能进行了较为详细的研究[5]。休斯敦莱斯大学P.S.Gandhi等人采用类似的测试台架对谐波传动的传动误差进行检测[6],试验装置中用扭矩传感器取代了H.D.Taghiradt设计的惠斯通应变电桥测扭矩的方法。Rached Dhaouadi等人采用同样的测试方法对谐波传动的传动刚度特性进行了研究[7]。国内许多学者也对谐波传动的系统特性进行了大量的研究,建立了各自适用的测试实验台[8-10]。
相对来说,国内关于谐波传动试验检测技术的专门研究则相对较少,特别是适用于真空等空间环境的试验检测技术更是少有涉及。目前,常用的谐波传动测试加载方式主要有磁粉制动器加载、液压加载、惯性负载和发电动机式等几种。磁粉制动器加载方式结构简单且扭矩调节范围大,但气隙中的磁粉在真空环境中会由于结块而无法产生正常的摩擦力,限制了其在空间环境下使用;液压式试验台采用液压系统加载,适用于大载荷,但其反应速度较慢,加载精度不高,不适用于紧凑型试验台的精确加载;惯量负载只能用于某些性能测试;发电动机式试验台利用电动机处于发电状态来加载,系统存在严重非线性缺陷,低速状态下精度不高,同时也存在散热问题。
本文针对空间环境适应性,结合使用单位需将试验台放置在模拟空间环境的真空罐内的要求,设计开发了一种全程计算机控制的谐波传动多参数测量的新型试验台——双伺服扭杆加载谐波传动试验台。
1 加载机构及工作原理
结构紧凑且适于放置在模拟空间环境的真空罐中是研制本试验台的出发点,提高测试系统的自动化程度是基本要求。经过比较试验,本文根据弹性材料的刚度具有良好的线性这一特点,选用弹簧钢材料制作扭杆作为试验台系统的扭矩加载机构。
扭杆起扭力弹簧的作用,安装在两台联动的伺服电动机之间,并与被测谐波传动产品相连。两伺服电动机通过相互间的转角差φ为扭杆施加扭转角度变形,产生扭矩,从而实现对被测产品的加载。扭矩大小与变形量成正比,动态地调整转角差φ,可实现对加载扭矩的动态控制。
依据所需加载载荷的大小,实验中选用了不同直径的扭杆,合理地配置扭杆杆径可以提高测试的精度并保证系统的安全性。图1给出了谐波传动试验台的工作原理图。
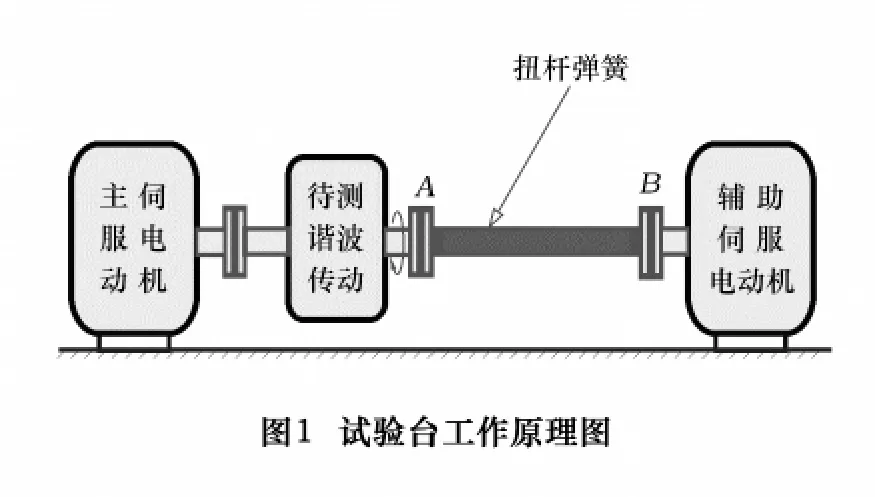
这种加载方式克服了磁粉制动器加载不适用于真空环境的不足,并且能够实现自动控制和同时测取多项产品参数,提高了测试效率。本系统可测试项目包括效率、传动精度、灵敏度与回零精度、刚度与回差、寿命、起动扭矩、超载、过渡过程等。
2 系统控制与数据采集
试验台的系统控制与数据采集是试验台电子测控系统的主要构成。工控机为试验台主控中心,Windows为系统软件运行环境,采用美国PMAC多轴运动控制卡控制两台伺服电动机的旋转速度与位置,扭矩传感器和角度编码器分别测取扭矩和角位移等信号,数据采集卡和计数卡实现物理量的收集。系统运动控制设计与系统数据采集设计如图2所示。

在试验台电子测控系统中,PMAC多轴运动控制卡用于与主机通信、接收系统指令在线编译并同时控制两轴进行样条插补。PMAC在电动机负载的情况下,通过对系统调试获得合理的PID控制参数,实现运动的位置闭环控制;通过内置变量设置,对受控电动机进行加速控制、速度控制和位置控制。试验台当下的运动状态由PMAC的查询功能实施监测,设置正负限位参数,保证系统的安全。
角位移和扭矩测量分别选用德国HEIDENHAIM脉冲式绝对角度编码器和德国HBM T20WN系列扭矩传感器,并安置多点温度传感器以监测试验台系统的环境温度。角度数据采集实现单轴或双轴同步,采集速度在一定范围内可由用户自主选择。根据输入与输出端角度信号对测量精度的影响,输入端采用分辨率为0.005°的旋转编码器作为角度测量元件,输出端采用分辨率为0.000 56°的角度编码器作为角度测量元件。扭矩测量所得输出轴的输出扭矩,既是1个被要求控制的信号,也是加载控制的反馈信号,主控中心据以调控两台电动机转角差,精确调节加载载荷。系统扭矩调整的算法核心是计算在当前弹簧刚度下应调整的角度差,图3给出了加载扭矩控制流程图。
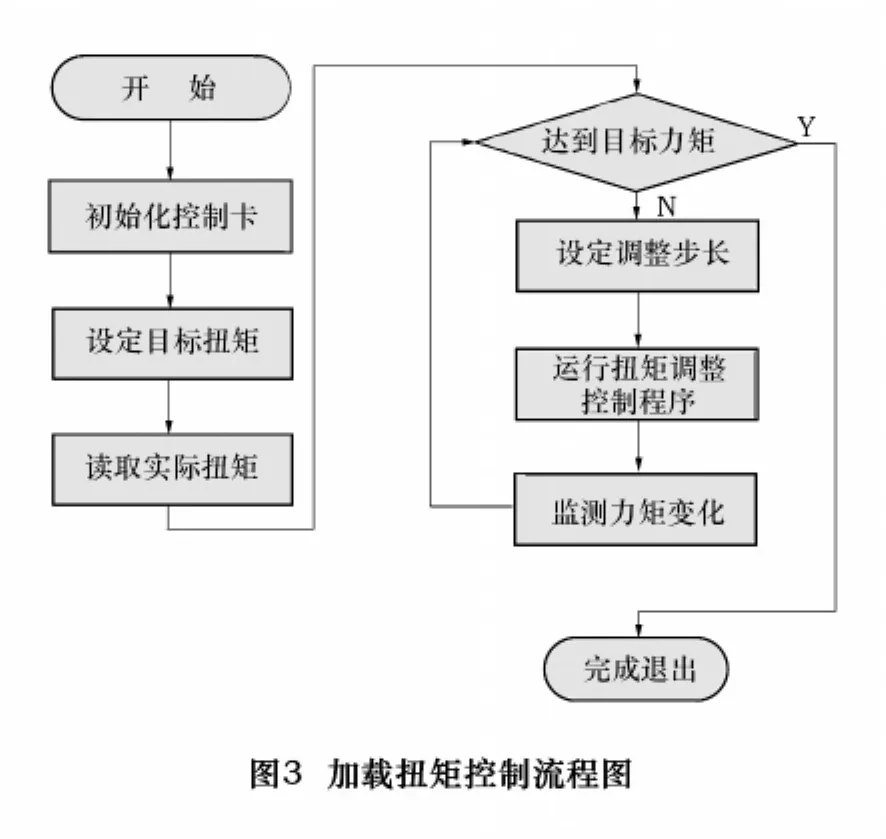

3 试验台测控系统软件
测控系统软件以Windows为运行环境,具有简明易用的可视化人机界面。测控系统软件通过运动控制卡对伺服电动机进行精确的同步控制,可对谐波传动特性同步自动地实现多路模拟量与数字量的信号采集。图4给出了系统软件功能模块框图。
4 试验台性能分析
4.1 扭杆特性实验
为验证本文所设计加载扭杆的特性,对扭杆进行18次不等距加载实验,加载最大扭矩为32 N·m。弹性扭杆设计刚度3.805 N·m/(°),实际测得扭杆刚度3.795 N·m/(°),如图5所示。在各测点处,实际扭杆刚度在理论值附近跳动,与理论刚度基本吻合,且在测试范围内,扭杆刚度基本保持线性。测试结果验证了本文所提出的扭杆加载方式的可行性。
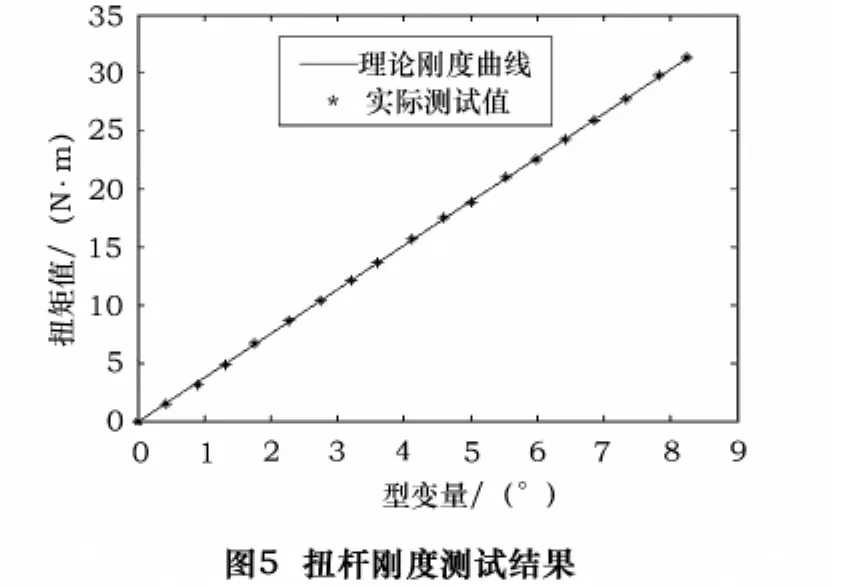
4.2 速度稳定性
PMAC通过F指令设定连续运行期间的固定速度。理论上,谐波传动在试验时应处于匀速转动状态;由于电气与机械的固有特性,实际上谐波传动的运行速度始终处在小幅波动中。波动幅度是系统稳定性的衡量指标。
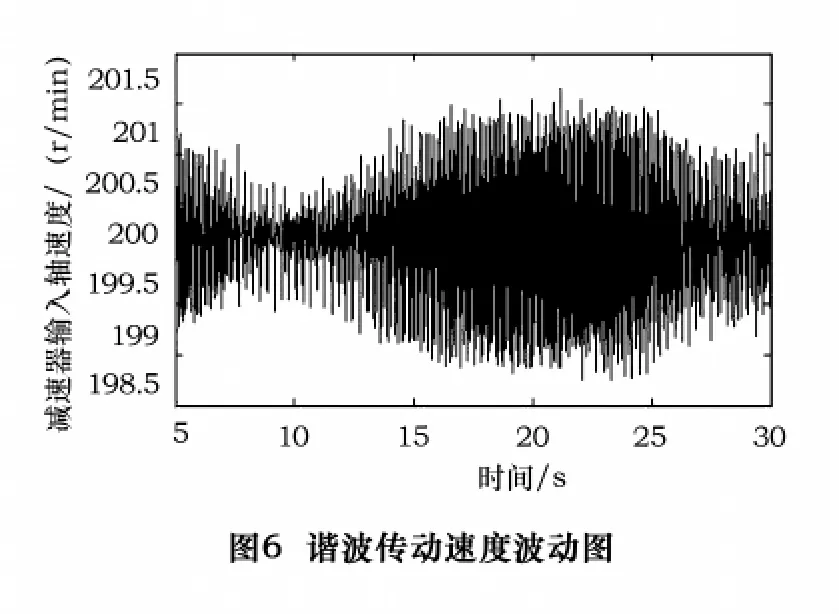
实测速度波幅时,输入轴设定以200 r/min运转,以1 kHz为采样频率,连续采样25 s,测量结果如图6所示。
试验结果显示:速度平均偏差率为0.18%,最大速度偏差率为0.693 1%。当谐波传动运行在额定速度下,速度的波动幅度较小,速度稳定性好。
4.3 扭矩稳定性
扭矩稳定性以系统运行速度的波动幅度为评测标准。实测时,额定速度200 r/min,对谐波传动输出轴扭矩信号进行1 kHz的快速采样,采样时间4 000 ms,得出相应扭矩时域波动图7。
试验给出扭矩平均偏差率为0.794%。试验台扭矩控制比较稳定,优于设计目标。

4.4 试验举例
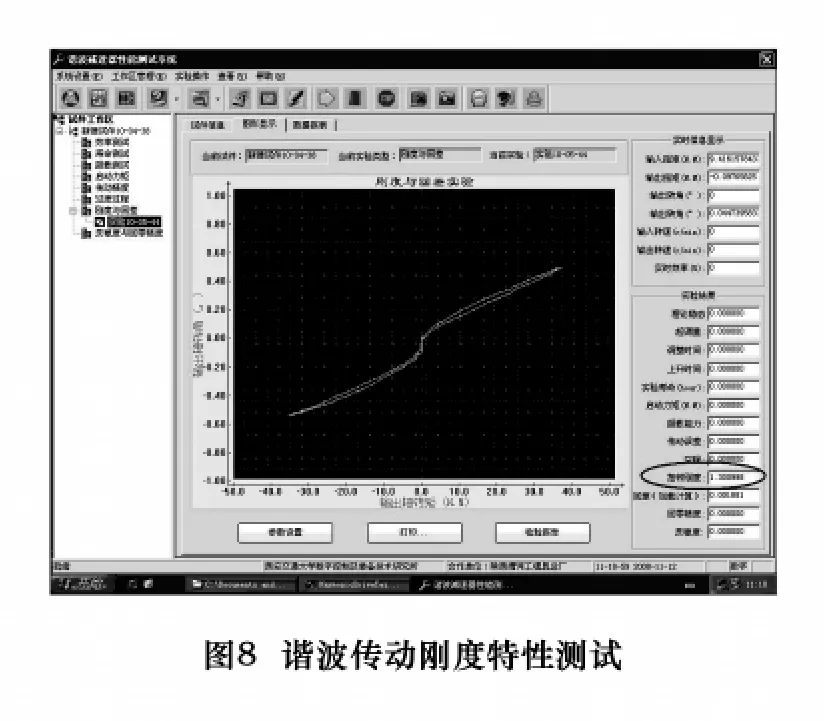
为测试本实验台性能,对某型号谐波传动进行了系列试验。图8是该谐波传动的刚度特性,测试程序按GB/T14118-93标准进行,测试过程中对被测谐波传动实施正向—反向—正向加载,分步长进行,加载起点为扭矩值为0 N·m,加载扭矩稳定时进行数据采集。图中,谐波传动在0 N·m负载附近,由负载引起的角度变形量较大,说明谐波传动柔轮和刚轮构件间存在间隙;越过这一区域后,谐波传动输出刚度基本呈线性。反向测试,刚度曲线与正向曲线之差反映了弹性变形引起的迟滞现象。系统拟合所得试件的输出刚度(图中圈处数值1.300 998)与设计值基本相符。
5 结语
本文基于增强空间环境适应性和提高自动化程度,研制了一种新型的谐波传动试验台——双伺服扭杆加载谐波传动试验台,为空间环境下谐波产品高效动态测试提供了一种新的选择。本试验台系统研制完成后,应用于某系列谐波传动动态参数的测试,经反复试验,证明了双伺服扭杆加载谐波传动试验台的可行性与实用性。对比现有的各种试验台的加载原理及设计思想,双伺服扭杆加载谐波传动试验台具有结构紧凑、可测参数多、控制简单、可靠性高、反应速度快、自动化程度高、环境适应性强等诸多优点。
双伺服扭杆加载谐波传动试验台系统经过适当的改造,也适用于其他旋转运动与扭矩传动产品的性能试验。
[1]Musser C W.The harmonic drive-breakthrough in mechanical drive design[J].Machine Design,1960,32(8):160-170.
[2]Krishnan S,Voorhees C.The use of harmonic drives on NASA's mars exploration rover[J/OL].NASA Center for Aero Space Information(CASI),19-Nov-2001.http://hdl.handle.net/2014/13269.
[3]Kazerooni H.Dynamics and control of instrumented harmonic drives[J].J Dyn Syst Meas Control,1995,3(117):9-15.
[4]Tuttle T D.Seering W P.A nonlinear model of a harmonic drive gear transmission[J].IEEE Transactions on Robotics and Automation,1996,12(3):368-374.
[5]Taghirad H D.Robust torque control of harmonic drive systems(PhD_thesis)[D].Montreal:McGill University,1997.
[6]Gandhi P S.A nonlinear observer for friction estimation and compensation in harmonic drives[C].Power Electronics and Drive Systems,2003.PEDS 2003,2003,11(1):259-263
[7]Ghorbel F H.On the kinematic error in harmonic drive gears[J].Journal of Mechanical Design,2001,123(1):90-97.
[8]沈允文,叶庆泰.谐波齿轮传动的理论和设计[M].北京:机械工业出版社,1985.
[9]辛洪兵,赵罘,秦宇辉.谐波齿轮传动系统非线形扭转振动分析[J].机械科学与技术,2005,24(9):1040-1044.
[10]黄蓉,何钺,唐建中,等.谐波齿轮振动探析[J].机械传动,1995,19(1):33-36.
