凸轮磨削动态特性影响的排除
2011-10-18刘兴富
刘兴富
(广州威而信精密仪器有限公司,广东广州510700)
随着节能、低碳、环保重要性的提升,对车辆燃油燃烧和废气成份的要求也日益提高。因此,除了对发动机零部件,特别是凸轮轴的凸轮在设计上不断进行研究之外,还必须提高其加工精度。在汽车行业中减小凸轮的加工误差,防止凸轮形状误差超差的现象,已是一个非常重要的课题。
在磨削凸轮时,影响凸轮精度的因素很多:如原始靠模(标准凸轮)、工作靠模等系统本身的设计和制造误差;仿形系统的间隙及弹性变形而引起的变形误差;磨床本身的精度误差以及被磨削凸轮的形状而引起的磨削动态特性所造成的形状误差。而凸轮磨削时的动态特性,是影响凸轮形状精度的一个重要因素。
1 凸轮形状的形成
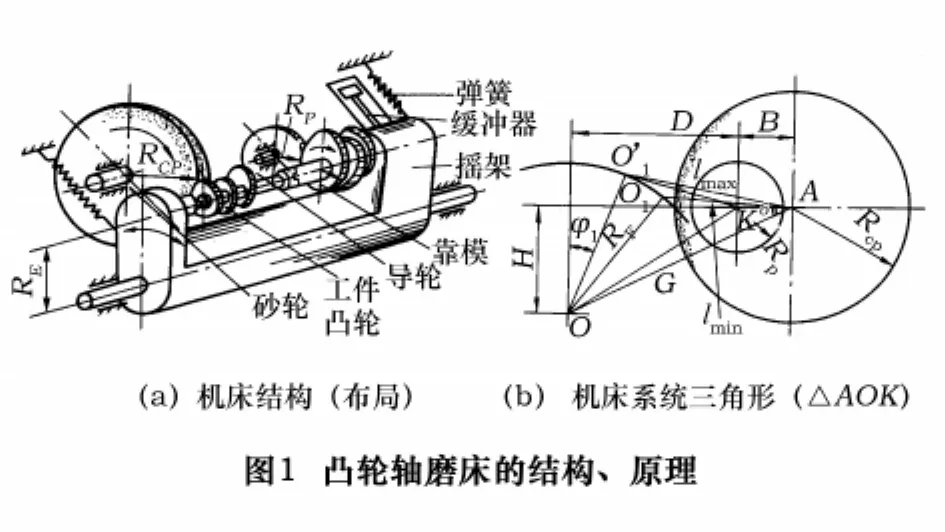
为了说明在凸轮磨床上磨出凸轮形状的过程,可以运用相对运动关系,把机床主轴的转动看成是机床系统围绕主轴作反向转动,因此,可以把磨削过程看成是凸轮和机床主轴不动,而是整个机床绕凸轮作反向转动。这时,砂轮中心按一定轨迹运动,磨出凸轮形状。当砂轮直径为定值时,机床系统三角形(△AOK)不变(见图1b),它的运动轨迹:砂轮中心A的运动轨迹保证了磨出凸轮合格形状,因此,凸轮形状是砂轮按其运动轨迹所作的一系列圆簇的包络线。
2 动态特性对凸轮形状的影响
在M8312型凸轮轴磨床上磨削凸轮时,除了受机床的系统刚性及几何精度的影响外,还受到摇架摆动的角速度及加速度的变化、弹簧张力的变化,磨削冲击、机床缓冲和阻尼装置的效果等动态特性的影响。如果只提高机床的几何精度,不排除机床动态特性的影响,是磨削不出合格的凸轮形状的。这里,就动态特性对凸轮形状精度的影响,作如下具体分析。
(1)桃尖下陷
尽管靠模的最大升程是理论正确值,但磨出的凸轮最大升程总是比理论值小(图2),这一现象称为“桃尖下陷”,下陷量一般为0.03~0.1 mm。
桃尖下陷的主要原因是,机床液压缓冲器的调节压力和弹簧的最小拉力配合不当所致。当液压缓冲器的压力为0.4 MPa时,凸轮的最大升程比理论值小0.1 mm;当把液压缓冲器的压力减小到0.15 MPa时则发现,开始进刀时仅在基圆段出现火花,而顶圆段不与砂轮接触,再进刀直至顶圆段出现火花,表明整个凸轮轮廓都与砂轮接触,凸轮的最大升程仅比理论值小0.02 mm。

上述现象从图3可以解释:在磨削凸轮桃尖时(图3a),由于升程逐渐增大,迫使摇架向外摆动,弹簧被拉长,拉力增大,液压缓冲器的活塞杆并未受到摇架的压力,只是在本身的液压作用下保持与摇架接触。在被拉长弹簧越来越大的拉力作用下,凸轮与砂轮接触良好,因而磨去了应当磨去的金属层。磨完桃尖后,由于升程逐渐减小,摇架在弹簧拉力作用下向内摆动(图3b),受到液压缓冲器活塞杆的阻力,弹簧的拉力也越来越小,如果缓冲器调节力大于弹簧的拉力,磨基圆及其附近时,有可能造成标准凸轮与导轮接触不上,没有磨去应当磨去的金属层,而形成靠模桃尖下陷。同理,磨削凸轮的过程中,上述现象又重新出现,两次桃尖下陷的叠加,致使凸轮桃尖显著下陷。

(2)左廓瘦右廓胖
磨出的凸轮总是左侧的升程偏小,右侧的升程偏大(图2),即出现“左廓瘦右廓胖”现象。
左廓是指磨削过程中摇架向外摆动时所磨的一侧轮廓(图4a);右廓是指磨削过程中摇架向内摆动时所磨的一侧轮廓(图4b)。
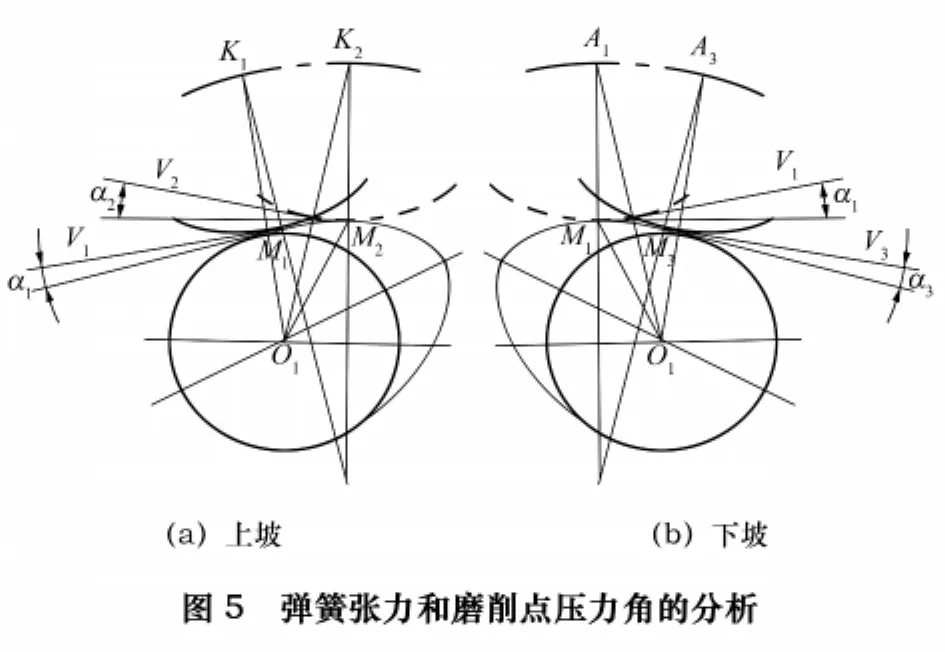
当磨削左廓时,凸轮的升程逐渐增大,迫使摇架向外摆动,弹簧拉力越来越大,缓冲器的阻尼不起作用,砂轮与凸轮接触点处的压力角也越来越大,形成上坡(图4a)。在压力角逐渐增大,弹簧张力也逐渐增大的情况下(图5a),有可能导致砂轮对凸轮的啃削,使左廓多磨去了一层金属,左侧升程值减小,形成左廓瘦。

当磨削右廓时,凸轮的升程逐渐减小,摇架内摆并受到缓冲器活塞杆阻尼力的抵抗,由于弹簧拉力和磨削点的压力角越来越小,形成下坡(图4b、图5b),导致砂轮和凸轮接触不良,没有磨去应磨去的金属层,因而右侧升程值增大,形成右廓胖。
3 动态特性影响的排除方法
要把凸轮磨削过程中机床诸动态特性的影响事先找出,并逐个予以排除,是一件非常复杂的技术工作。采取这样排除动态特性影响的作法,是不可取的。在现有生产设备条件下,运用动态特性规律修正靠模的方法是可行的。但是,在靠模上找出与凸轮的对应点,由于凸轮轴磨床采用了摇架结构,使得靠模升程与凸轮升程不是呈线性关系,因此,即使掌握了靠模修正技术,且有丰富的经验,也不易做到准确无误。特别是当凸轮的升程在某点出现负值误差时,为修复超差点要修正靠模的整个轮廓。这对于淬硬的靠模来说,工作量相当大,往往得不偿失。
另一种方法是,根据磨削出的凸轮升程误差的规律性,通过修正原始靠模(标准凸轮),进行再次反靠,即“补偿反靠”。这种方法不直接修正靠模本身,而是通过对标准凸轮补偿,间接地对靠模进行修正,就可以磨出合格的凸轮。
原始靠模(标准凸轮)补偿量和期望值求解(测算)的具体方法、步骤如下:
如果机床系统刚性可靠,几何精度稳定,只要依据“反靠”、“磨削”过程中工件凸轮升程误差的规律性,通过对标准凸轮的修正,就间接地排除了机床诸动态特性的影响。
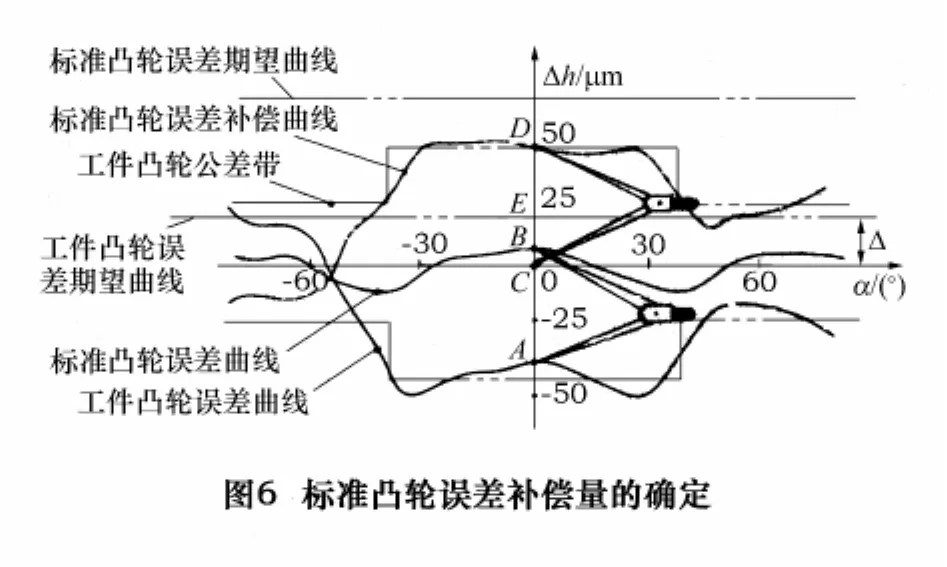
“反靠”后,测量标准凸轮、工件凸轮的升程,在直角坐标系中画出标准凸轮、工件凸轮的升程误差曲线(图6),并按如下作图方法,作出标准凸轮的误差补偿曲线和误差期望曲线:用两脚规量取标准凸轮升程误差曲线与工件凸轮升程误差曲线间的距离,再以横轴为基准反向得到点D,即|CD|=|AB|,D点就是标准凸轮误差补偿曲线上的一点。如果以工件凸轮误差期望曲线(与标准凸轮误差曲线间的距离为△的曲线)为准反向得到点F,即|EF|=|AB|,F点就是标准凸轮误差期望曲上的一点。当在曲线上按一定的角度间隔取点量取,并将各点连接成曲线,就得到了标准凸轮的误差补偿曲线和误差期望曲线。
在“反靠”过程中,当工件凸轮升程误差曲线落在标准凸轮升程误差曲线的下方时,说明机床动态特性产生的是一负误差,标准凸轮升程补偿量和期望值应为一正值;当工件凸轮升程误差曲线落在标准凸轮升程误差曲线的上方时,机床动态特性产生的是一正误差,标准凸轮升程补偿量和期望值应为一负值。
原始靠模(标准凸轮)补偿量和期望值,也可用解析方法来计算。
工件凸轮升程误差曲线与标准凸轮升程误差曲线间的距离AB,就是标准凸轮升程误差的补偿量S,即

标准凸轮升程误差的期望值Q为
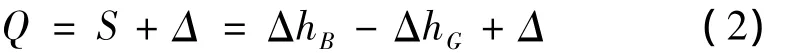
式中:ΔhG为工件凸轮的升程误差;ΔhB为标准凸轮的升程误差;Δ为工件凸轮升程误差的期望值,即“补偿反靠”工件凸轮所期望的升程误差曲线离开横轴的距离。
“补偿反靠”时,修正标准凸轮的升程(刮削修正标准凸轮的升程表)为

式中:hX为修正标准凸轮的升程;hL为工件凸轮的理论升程。
按上述方法在1台M8312型凸轮轴磨床上制造凸轮靠模时,只进行了1次补偿,用了1周时间,就制造出了合格的凸轮靠模。也就是说,凸轮磨削中动态特性的影响已被排除了,从而磨削出了合格的凸轮。和已往手工方法要用3个月的时间相比,工效提高了10倍以上。这充分说明排除机床动态特性影响的新方法是行之有效的。
[1]刘兴富,李长星.凸轮轴的自动测量及数据处理评定方法(1)[J].摩托车技术,2006(5).
[2]刘兴富,李长星.凸轮轴的自动测量及数据处理评定方法(2)[J].摩托车技术,2006(6).
[3]苏步青,华宣积,忻元龙.实用微分几何引论[M].北京:科学出版社,1986.
[4]刘长安,王怀生.数值计算的理论和方法[M].西安:陕西人民出版社,2000.
