基于查找表的BCH码快速译码算法

孔 挺，宫 芳，方扬扬

(1.哈尔滨工程大学信息与通信工程学院，哈尔滨150001;2.海军飞行学院教研部，辽宁葫芦岛125001)

在通信系统和计算机系统中，为了发现和纠正信号传输、存储过程中的错误，需要在系统中采用信道编码技术对信息进行处理，以提高系统的可靠性.在各种信道编码中，由于BCH码具有严谨的代数结构，构造简单，纠错能力很强，尤其在中短码长情况下，它的性能接近香农极限.因此，在实际应用中得到了广泛的应用.在BCH码中，BCH(31，21)码的整个码字加上1位奇偶校验后，刚好可以形成32位码长的扩展BCH码，很适合16位或32位计算机处理[1]，因此，本文以BCH(32，21，5)码为研究对象，基于BCH码的传统查找表译码算法，介绍一种在译码速度和资源消耗上均有更优异表现的快速查找表译码算法.

1 BCH码编译码理论

1.1 BCH码编码原理

由纠错码理论可知，BCH码属于循环码的一个子类，而循环码又是一种线性分组码，记为(n，k)码，其中:n表示码字长度，k表示码字中信息位的长度.所以BCH码的编码实现可以有两种方法:一种是用常规线性分组码的构成方法，即将k位待编码的信息码字与其(k×n)维的生成矩阵相乘后得到n位编码码字;另一种方法是利用循环码的循环移位自闭性的特点，即:若是一个码字，则它的循环移位)也是一个码字，采用模多项式的方法进行编码，这种方法更为方便，也是目前常用的方法.具体来说就是将以信息码组)作为各项系数的多项式与相乘后对BCH码的生成多项式g(x)求余，得到余式r(x)，r(x)的系数即为需要加入的冗余校验位(或称监督位)，将信息码组与校验位前后连接，就可以得到常用的系统BCH码字多项式)，其中多项式C(x)中的各项系数即为信息码组所对应的BCH编码码字，所以这种BCH码编码方法的实质就是以生成多项式g(x)为模的除法问题，在实际应用中通常利用LFSR(线性反馈移位寄存器)就可以很方便地实现BCH码的编码[2].

1.2 BCH码的译码

相对于BCH码的编码而言，BCH码译码则要困难得多.传统的BCH码译码一般会采用迭代或者查找表两种方法.常见的迭代算法包括Berlekamp-Masssey算法、Pereson算法、Step-by-step算法等[3].虽然这些算法硬件资源消耗较少，但是它们设计复杂度较高，译码速度慢，而且不易于硬件实现.而查找表译码算法与迭代译码算法相比，具有译码速度快，硬件实现简单的特点，只要一块ROM建立伴随式图样和错误图样的对应表，通过查找与伴随式S相同的图样，即可找到对应的错误图样，得到错误位置，从而进行纠错[4].但是此算法对于短码比较有效，当码字很长或纠错位数较多时，其缺点也是明显的，即需要占用大量的硬件资源.因为本文重点研究BCH码的查找表译码方法，所以对迭代算法不做讨论，仅讨论查找表译码算法.

查找表译码算法法实际上就是根据接收码字R的伴随式S与错误图样E的对应关系，建立起S与E的查找表.对于二进制系统码的校验矩阵H，由S=RHT可得S与H中列向量的对应关系，进而可以确定出错误位置并进行纠正.原理如下[5].

假设发送的码字序列为C=(c1c2…cn)，码字在信道中产生的错误序列为E=(e1e2…en)，则接收端收到的码字为R=C+E=(r1r2…rn)，伴随式序列由S=R×HT=(C+E)×HT=E×HT得到.

1)当S=0时，e1=e2=…=en=0即E=0，R=C，说明此时未发生错误.

2)当S≠0时，则说明e1，e2，…，en不全为0，此时有错误发生.根据伴随式的值与H中列向量的对应关系，可得以下结论:

当发生一位错误时，假设错误位置在码字的第i位，则有ei=1，el=0(l=1，2，…，n，l≠i)，于是S向量必与H矩阵第i列向量相等，利用这一关系可以找到接收向量R中的错误位置.

当发生两位错误时，假设错误位置在码字的第i位和第j位，则有ei=1，ej=1，el=0(l=1，2，…，n，l≠i，j)，于是S向量等于H矩阵内第i和第j列向量的模2和，且这两列的取法是惟一的.利用这一关系可知R向量的两个错误位置.依此类推，根据S向量与H中列向量的对应关系，只要满足BCH码纠错能力，BCH码就可纠正R中的多个错误.因为是二进制码，找到错误位置后，随即就可以纠正.

BCH码传统查找表译码结构示意图如图1所示.

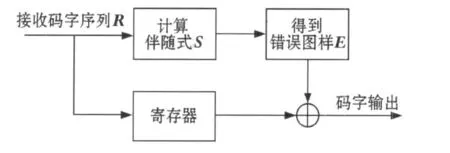
图1 BCH码传统查找表译码结构示意图

下面以(31，21，5)BCH码为例，介绍查找表译码算法的理论基础.(31，21，5)BCH码的生成多项式为

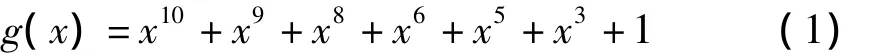
对应的系统码生成矩阵为

可以看出该生成矩阵的形式为G=(Ik，p)前面的部分为单位阵，这样得到的码字前k位为信息位，后n-k位为校验位.设信息序列为M=(m1m2…mk，生成码字为C=M×G(c1c2…cn).假设码字在传输过程中产生的错误图样为E=(e1e2…en)，则接收端收到的码字序列为R=C+E=(r1r2…rn).根据校验矩阵H与生成矩阵G存在的关系，可得(31，21，5)BCH码的校验矩阵为

首先计算伴随式，即S=R×HT.然后通过S得到错误图样E.因为(31，21，5)BCH码可以有效纠正2个以内的错误，所以利用上述传统的查找表译码算法，需要存储码字中发生1到2位错误时的所有图样.发生一位错误有31种情况，发生两位错误有465种情况，所以传统查找表译码算法需要存储组错误图样及其对应的伴随式.

2 BCH码快速查找表译码算法

从以上分析可知，传统的查找表译码算法虽然译码简单、快速，但是需要的存储空间比较大.为了实现译码资源与译码速度间具有良好的平衡，本文对传统查找表算法进行改进，提出一种在译码时间和资源损耗上均有良好表现的快速查找表译码算法.

2.1 快速查找表算法原理

为了节省存储资源，这里提出的改进算法是利用查找表和计算伴随式的汉明重量判断接收序列的错误位置.新算法的查找表内只需存储信息位发生任意可纠正错误时错误图样及其对应的伴随式图样.以(31，21，5)BCH码为例，其信息位为21位，若将信息出错时的错误图样(31bits)与其对应的伴随式图样(10bits)合称为查找表图样，则只需要存储组查找表图样就可以完成译码，其中一个查找表图样需要消耗bytes的存储单元.

假设(31，21，5)BCH码接收码字序列为R=(r1r2…r31)，在接收到的码字只发生2个以内错误的前提下，即在码字的纠错能力范围内，计算伴随式为S=R×HT=E×HT=E×[PTI10].借鉴传统查找表的思想，应该等于矩阵中某些与错误位置对应的列的模2和，这样，快速查找表算法对接收码字序列错误位置的判断可分为下列3种情况.

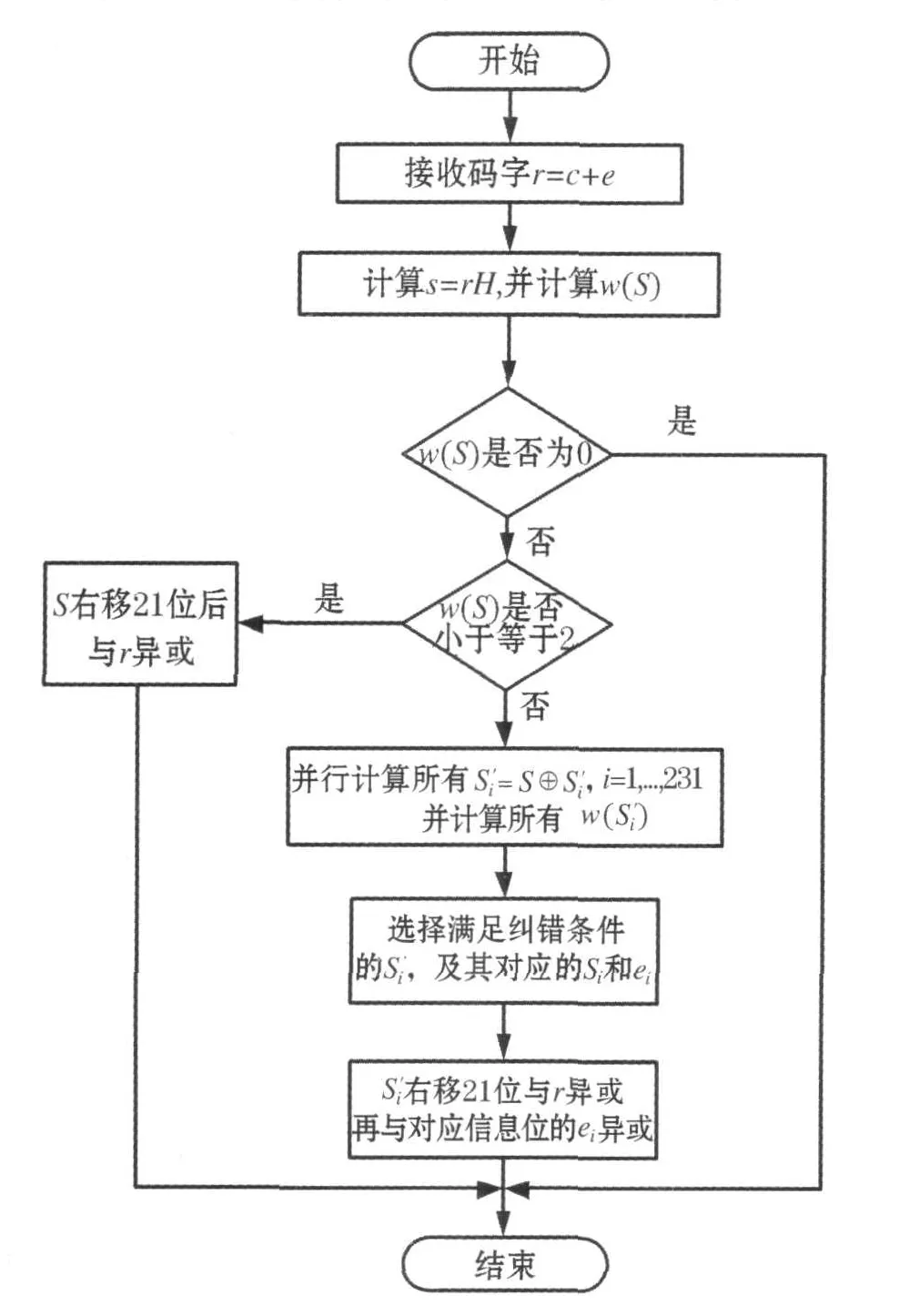
图2 (31，21，5)BCH码快速查找表算法流程图

1)当信息位不发生错误，校验位发生错误时，因为H的后半部分为单位阵，所以校验位r22…r31中发生1位错误时，伴随式S的汉明重量w(S)为1;校验位发生2位错误时，伴随式S的汉明重量w(S)为2.且S中1的位置与r22…r31中错误的位置对应，所以可以直接进行纠错.

2)当信息位发生错误，校验位不发生错误时，S的汉明重量w(S)肯定大于等于3.由于码字中仅当信息位出现2位以下错误时的伴随式图样和错误图样已经存储在查找表中，所以只要对查找表进行搜索即可得到错误图样，从而进行纠错.

3)当信息位和校验位同时发生错误时，假设信息位发生1位错误，校验位也发生1位错误时，S与查找表中对应于信息位错误的伴随式图样Si相减后，得到的差Si的汉明重量应该为1，且中1的位置与码字校验位中错误的位置对应.

2.2 快速查找表算法译码步骤

根据快速查找表译码算法的原理，(31，21，5)BCH码的译码流程如图2所示.

其具体译码步骤如下:

第1步:接收码字序列r;

第2步:计算伴随式S及其汉明重量w(S);

第3步:判断w(S)是否为零，如果是，转向最后一步;

第4步:判断w(S)是否小于等于2，如果是，将S向右移21位与r求模2和后转向最后一步;

第5步:将S与查找表中所有错误图样ei(i=1，2，…，231)对应的伴随式Si分别进行求模2和得，并计算每个的汉明重量;

第8步:译码结束.

3 仿真与性能分析

3.1 算法正确性的仿真验证

本文在Matlab环境下对快速查找表译码算法进行了验证.仿真模型如图3所示.

图3快速查找表译码算法的M atlab仿真验证模型

图3 中，msg1是由Matlab[6]中的函数随机生成的21位待编码信息位，然后对其进行(31，21，5)BCH码编码后，随机添加2位以下的随机错误，用快速查找表译码算法进行译码，最后删除校验位得到译码后的21位信息位msg2.

按上述条件与方法进行仿真验证后可知，msg2始终等于msg1，说明快速查找表译码算法可以对(31，21，5)BCH码发生的2个以内的所有错误进行有效译码.

3.2 译码时间的仿真对比

为了验证本文提出的改进算法在译码速度上的优势，本文在Matlab环境下对(31，21，5)BCH码分别采用快速译码算法和传统查找表译码算法时的译码时间进行了蒙特卡洛仿真，仿真计算机性能为:Intel(R)Core(TM)2 Duo CPU T6500 2.10GHz 2GB内存，Matlab仿真模型如图4所示.

图4 验证不同译码方法的译码速度的M atlab仿真模型

图4 所示模型中，将图3中的加错过程改为将编码后的码字经BPSK调制、AWGN加噪，后得到接收码字，解调后，再用不同的译码方法译码，删去校验位后得到msg2.按上述过程进行10万次验证后得到两种译码方法的译码时间如表1所示.

表1 快速查找表法与传统查找表法译码时间对比

从表1中的数据可以看出，采用本文提出的快速查找表算法由于在译码时需要查找的错误图样较少，在译码速率上能比传统查找表算法快28.81%.因此，本文提出的快速查找表算法在译码速度上具有较大的优势.

3.3 存储资源消耗对比

从资源消耗这方面来看，本文提出的快速查找表算法，由于只存储了信息位发生错误时的图样及其对应的伴随式图样，相比于传统的算法，可以节省大量的存储空间.表2列出了(31，21，5)BCH码在两种不同算法下占用的存储资源.

表2 不同查找表算法对应的查找表图样个数

从表2中可以看出，相比于传统查找表算法，对(31，21，5)BCH码采用本文提出的算法，可以节省53.4%的存储资源.

从以上性能分析可知，与传统查找表相比，本文提出的快速查找表译码算法在速度和资源损耗上均有较大的优势.

4 结语

本文以(31，21，5)BCH码为例，介绍了一种BCH码快速查找表译码算法，该算法在查找表中仅存储信息位发生错误时的错误图样及其对应的伴随式图样，并结合接收码字伴随式的码重进行译码.与传统查找表相比，该算法由于需要查找的错误图样较少，不仅提升了译码速度，而且节省了存储资源，对中短码长的BCH码而言，是一种在译码速度和资源损耗上均具有较好表现的译码算法.

[1]李心广.一种BCH码的软件译码的实现[J].无线电通信技术，1999，25(4):53-55.

[2]李志国，张伟功.BCH码迭代译码算法及软件实现方法[J].计算机技术与发展，2007，17(4):171-174.

[3]LIN S，COSTELLOD J.差错控制编码[M].晏 坚，译.2版.北京:机械工业出版社，2007:130-153.

[4]周盛容，胡正飞.基于BM迭代的高速BCH译码方法[J]..电脑知识与技术，2007(4):1019-1023.

[5]MASAHICHIKISHI，YIN K X，HIROSHI IWATA，et al.Consideration on System Capability Characteristics of Protable 2Mbps/8 Mcps CDMA with Phase Continuous QPSK[C]//Proc IEEE VTC98，[S.l.]:[s.n.]，1998，2:924-928.

[6]孙 屹，李 妍.Matlab通信仿真开发手册[M].北京:国防工业出版社，2005:1-218.