A ToyM odel for 3∶2∶1 Ratio of HFQPOs in XTE J1550-564

Ye Yongchun,H uang Changy in,L eiW eihua,W ang D ingx iong

(School of Physics,Huazhong U niversity of Science and Technology,W uhan 430074,China)

A ToyM odel for 3∶2∶1 Ratio of HFQPOs in XTE J1550-564

Ye Yongchun,H uang Changy in,L eiW eihua,W ang D ingx iong

(School of Physics,Huazhong U niversity of Science and Technology,W uhan 430074,China)

Based on a toy model of coexistence of the Blandford-Znajek(BZ)and magnetic coupling(M C)processes w ith a non-axisymmetric magnetic field,we explain a puzzling 3∶2∶1 ratio of the high-frequency Q uasi-Periodic O scillation(HFQ PO)in XTE J1550-564.It turns out that two frequencies of the HFQ PO can be fitted by two rotating magnetic hotspots arising from theM C process,and the other HFQ PO frequency is related to a magnetic hotspot produced in the BZ process.Furthermore,we discuss the astrophysical environment based on the correlation between HFQ PO s,jet and state transition in XTE J1550-564.

accretion;accretion discs;black hole physics;X-rays:stars;magnetic field;instabilities;oscillation

1 Introduction

Since the launch of the NA SA satellite Rossi X-Ray T im ing Explorer(RXTE)a number of high-frequency Q uasi-Periodic O scillations(HFQ PO s)have been discovered in several X-ray Binaries (XRBs), and they often appearas transient and subtle features in the Fourier power density spectra,w ith centroid frequencies of tens to hundreds of Hz and low rm s amplitude values(1%～3%) stronglydependent on theenergy range[1,2]. In particular,seven black hole (BH)XRBs exhibit transient HFQ PO s,of which four sources have pairs occurring in GRO J1655-40(450 and 300 Hz)[3,4],H1743-322(241 and 165 Hz)[5],GRS 1915+ 105 (168and113 Hz,67and 41Hz)[6,7]and XTE J1550-564 (184 and 276Hz)[8-10]w ith a puzzling 3∶2 ratio of the upper frequency to the lower frequency.

A lthough anumber of models havebeen proposed to explain the HFQ PO pairs in BH XRBs in the last decade,no consensus has been reached on the physical origin of these HFQ PO pairs.A s mentioned by some authors,there exists 3∶2∶1 frequency ratio of HFQ PO s(276,184,92 Hz)in XTE J1550-564[10,11].Furthermore,HFQ PO s are associated w ith the steep power-law(SPL)state in BH XRBs(for a review see ref.[12]). These features challenge all HFQ PO models,in which the magnetic hotspot model is included[13,14].

In this paper,we intend to interpretthe 3∶2∶1frequency ratioof HFQ PO sinXTE J1550-564 and clarify the correlation between HFQ PO s and state transition by virtue of nonaxisymmetricmagnetic coupling (M C) ofa rotating BH w ith its loads,in which the remote astrophysical load and the surrounding accretion disc are included.

This paper is organized as follow s.In Section 2 we give a brief description of the model. In section 3,we fitthe three frequencies ofthe HFQ PO s in XTE J1550-564,i.e.,276,184 and 92 Hz,to three rotating magnetic hotspots,among which one(276 Hz)is related to the BZ process,and the other two(184 and 92 Hz)arise from the M C process w ith the screw instability ofthe magnetic field. In section 4 we discuss the constraintof the 3∶2∶1 frequency ratio of HFQ PO s to the astrophysical environment of XTE J1550-564. In section 5 we summarize our main results.Throughout this paper the geometric unitsG=c=1 are used.

2 M odel description

Based on several assumptionsaboutnonaxisymmetric magnetic field given in ref.[14],we proposed a magnetic field configuration as shown in Figure 1.

In Figure 1,the large-scale magnetic field at the BH horizon consists of the open and closed field lines w ith an angular boundary atθMC.The open field lines transfer energy and angular momentum from theBH to the remote loads in theBZ process,while the closed field lines transfer those from the BH to the accretion disc via theM C process.

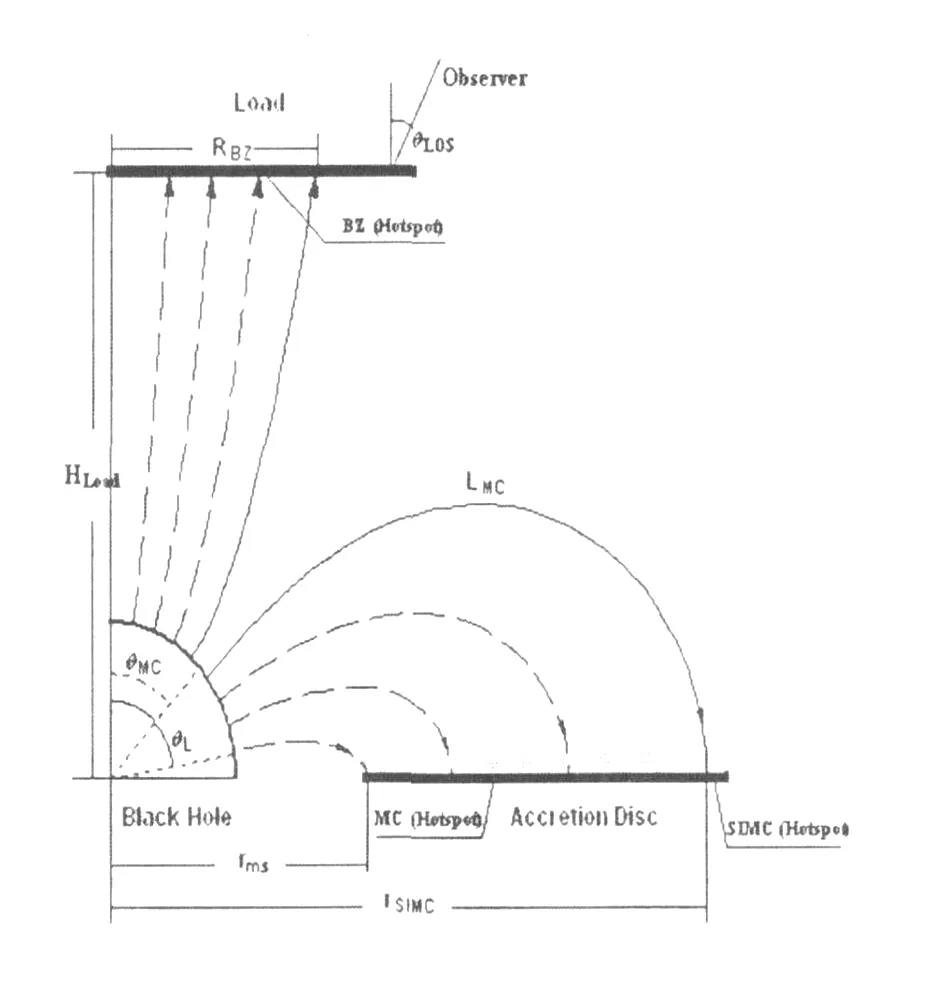
Fig.1 A schematic draw ing for the configuration of the poloidal magnetic field w ith screw instability in BH magnetosphere图1 黑洞磁层中具有螺旋不稳定性的极向磁场位形示意图

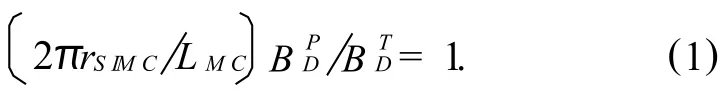
The equation (1)is derived based on the Kruskal-Shafranov criterion,where the radiusrSIMCcan be regarded as the outer boundary of the M C region,andLMCis the critical length of the poloidal field line for S IM C.The quantitiesBPDandBTDare the poloidal and toroidal components of the magnetic field on the disk,respectively.

The BZ and M C powers in non-axisymmetic case are related to those in axisymmetic case given in ref.[13]as follow,

A ccording to the Kruskal-Shafranov criterion,the screw instability of the large-scale magnetic field w ill occur,if the magnetic field line turns around itself aboutonce[15,16]. W ang et al[17]discussed the screw instability occurring in theM C process(henceforth S IM C),and the radiusrS IM Ccan be determ ined by the follow ing equation,whereandare the powers in nonaxisymmetic case,andandare the powers in axisymmetic case,respectively.

The powersandare given by W ang et al.as follow[18],

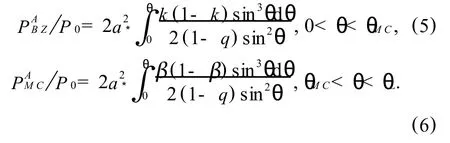
In equations(5)and(6),the parameterskandβare the ratios of the angular velocities of the open and closed magnetic field lines to the angular velocity ofthe BH horizon, respectively. The quantityis a function of the BH spin,andP0are defined as

whereB4is the strength of the poloidal magnetic field on the horizon in units of 104gauss,andmB His defined asmBH=M/M○·.

So far seven parameters are involved in our model,in whichmBHanda＊are used for describing the mass and spin of the Kerr BH,the power-law indexnis for the variation of the magnetic field w ith the radial coordinate of the disc,kis for the angular velocities of the magnetic field lines in the BZ process,and the three parameters,B4,δand∈are used fordescribing the non-axisymmetric magnetic field on the horizon as defined in refs[13]and[14].Throughout this paper δ=0.5,∈=0.2 are assumed in calculations.

3 Three magnetic hotspots for 3∶2∶1 ratio of HFQPOS

A s argued in ref.[14], the M C process produces a hotspot in the inner disc due to the nonaxisymmeticM C,and the second magnetic hotspot arises from the screw instability.A nd the two frequenciesandare related to the corresponding Keplerian angular velocity as follow,

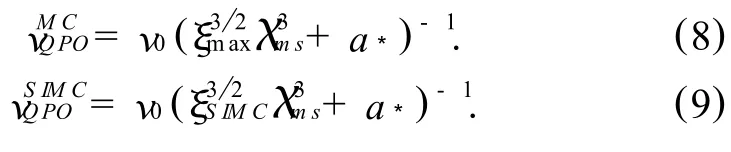
In equations(8)and(9) ν0is defined as ν0≡(mBH)-1×3.23×104Hz,χmsis related to the radius of the inner edge of the disc bythe parameterξmaxis related to the radiation flux due to disc accretion and theM C process as argued in ref.[14],and ξSIMC≡rSIMC/rm sis determ ined by the criterion(1)for the screw instability.

Now we discuss the origin ofthe third magnetic hotspot by invoking the BZ process.Follow ing Fendt[19],we assume that the poloidal magnetic field on the remote load varies asBL/BH=e-αx,wherex≡R/rHis the cylindrical radius in term s ofthe radius ofthe BH horizon, the parameterαis used to indicate the variation of the magnetic field w ith the radial coordinate of the load,andα=1.3 is assumed in calculations.Based on the conservation of magnetic flux,we have

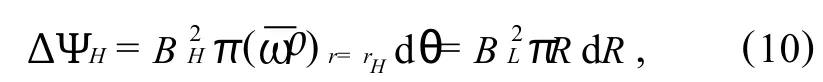
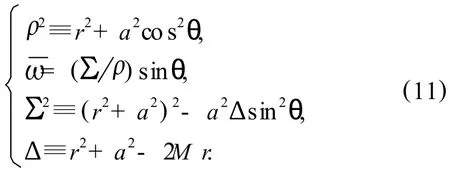
Integrating equation(12),we obtain the mapping relation between the angular coordinateθon the BH horizon and the cylindrical radiusxas follow s,

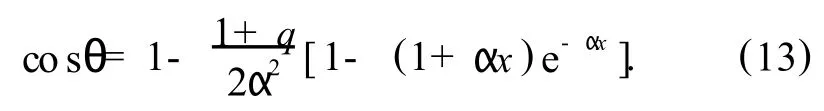
A s shown in Figure 1,the field line connects the angleθM Cat the horizon w ith the radiusRB Zat the load,and we have the relation betweenθMCandxB Zas follow s,

Combining equations(5)and(10)～(14),we have

Incorporating equations(13)～(15),we have the curves of dP~ABZ/dxversusxfor the givena＊andkas shown in Figure 2.

Fig.2 Curves of dP~ABZ/dxversusxw ithk=0.5 fora＊=0.6,0.7 and 0.8 in solid,dashed and dotted lines,respectively图2 dP~ABZ/dx随x变化的曲线,其中,k=0.5,a＊=0.6,0.7和0.8分别对应于实线,虚线和点线

A s shown in Figure 2,dP~ABZ/dxvaries nonmonotonically w ith the increasingx,and attains itspeak value between the innerand outer boundaries of the BZ region in the remote load.Combining the non-axisymmetric magnetic field w ith the non-monotonical profile of dP~ABZ/dx,we infer that the third magnetic hotspot is produced in

the BZ load,and the third HFQ PO frequency is= ΩF/2π,where ΩFis the angular velocity of the open field lines connecting the BH horizon and the BZ load.

Based on the equivalentcircuitgiven by M acDonald and Thorne[20]we have the relation betweenΩHandΩFas follow s,

whereΔZHand ΔZLare the resistances of the BH horizon and the load,respectively.Thus we find the ratio ofΩFto ΩLis closely related to the ratio of ΔZHto ΔZLas follow s,

The HFQ PO frequency corresponding to the third magnetic hotspot is given as follow s,

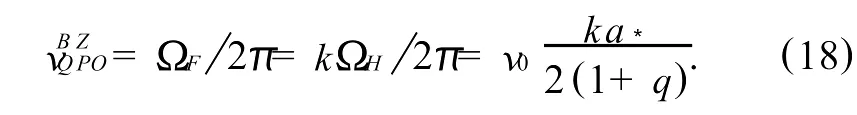
Therefore we can fitthe threeHFQ PO frequencies in XTE J1550-564 based on equations(8),(9)and (18)by adjusting the concerned parametersa＊,nandkfor the upper and lower lim its to the BH mass as shown in Table 1.

Tab.1 The 3∶2∶1 ratio of HFQPO s produced by the three magnetic hotspots for XTE J1550-564表1 3个磁热斑产生的黑洞双星XTE J1550-564的高频准周期振荡的3∶2∶1频率比

4 Requirement for astrophysical envionment

A s is well known,HFQ PO s of XRBs are observed in the steep power law (SPL)state,which could transit from a low/hard(LH)state w ith an explosive jet[7,9,21,22].

W ang, Dai& L u[23]suggested that the interaction between the jet and the surrounding interstellar medium can be used to explain the dynam ical evolution and radiation of the large-scale X-ray jets from XTE J1550-564.M otivated by this work we discuss the requirement of the 3∶2∶1 ratio of HFQ PO for the astrophysical environment of XTE J1550-564.

4.1 Requirement for surfaceresistivity of astrophysical load

Incorporating equations(17)and(18)w ith the results of Table 1,we find that the HFQ PO frequency corresponding to the third magnetic hotspotis closely related to the resistance of astrophysical load as follow s,The values of ΔZL/ΔZHare equal to 1.488 and 1.646 for the lower and upper lim its of the BH mass listed in Table 1,respectively.This result implies that the surface resistivity of theastrophysical load is of the same order as but a little greater than that of the BH horizon.

4.2 Requirement for block of astrophysical load

The astrophysical load(the BZ load)can be regarded as a medium shell surrounding the BH,on which the energy extracted via the BZ process could be released. Thus the transitions between LH and SPL states are related to the blocking states of the medium shell,and the association of Q PO (jet)w ith the SPL (LH)state can be interpreted as follow s.

A strong block corresponds to SPL state w ith Q PO,and a weak block corresponds to LH state w ith jet.It is the blocking of themedium shell that results in the absence of the jet,and meanwhile provides ascreen displaying thethird rotating hotspot.On the other hand,it is the breakthrough of the medium shell that results in the presence of the jet w ith the absence of the third rotating hotspot. In addition, the cooling of the Comptonization in medium shell could be helpful to interpret the hardness difference between the LH and SPL states.

The above discussion on the effects of the medium shell surrounding the BH of XTE J1550-564 can be summarized in Table 2.

Tab.2 Correlation of state transition w ith the blocking of the medium shell above the BH accretion disc表2 黑洞双星态转变与黑洞吸积盘上方介质壳层遮挡的相关性

Furthermore,in order to describe the astrophysical characteristic of the medium shell,we calculate some physical parameters about the shell.The expression for the surface resistivity of the BH horizon as follow s,

From equation(2)we obtain the upper lim it of ΔZH.A nd combine(17),(20)and the parameterkin Table 1,we obtain the upper lim it ofΔZL.

A s argued in ref.[24],the orbital inclination angle in XTE J1550-564 is about 67°～ 77.4°,which means that the angle between line of sight(LOS)and the normal of disc is 12.6°＜ θLOS＜ 23°asshown in Figure1. Considering the three hotspots corresponding to 3∶2∶1 ratio of HFQ PO s are observed at the same time[11],we think that the hostspots on disc cannot be kept out by the load(medium shell),and the geometrical relation between the boundary of the loadRB Zand the height of the loadHLoadmust be satisfied as follow s,

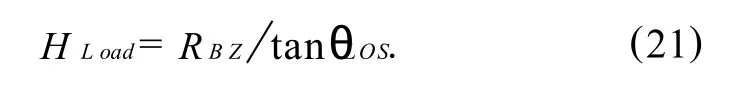
Incorporating equations(14)～(21),we have the upper lim it ofHL oadandΔZLand the lower lim it of them as shown in Table 3.

Tab.3 Physical parameters of the medium shell in XTE J1550-564:HL oadandΔZL表3 黑洞双星XTE J1550-564的介质壳层的物理参数:HLoad和ΔZL

Inspecting Table 3 we find that the medium shell is probably not far from the BH horizon(abouttens of gravitational radius),butthis conclusion could be a clue to the image that there exists a bubble in XTE J1550-564. A nd the resistivity of the medium shellm ight be about tens of ohm,which may be in favor of understanding the component of medium in XRBs.

On the other hand,from equation(5)we have the curve ofPBZ/P0versusnfor the givena＊as shown in Fig.3.In our calculation,assum ingB4～104andmBH=10,the strength ofBZ power is about～1036erg/s,which iswell fit the jet power of XTE J1550-564[21]. This conclusion show s that BZ process could supply enough energy for the formation of jet after the medium shell is broken.

Fig.3 Curves of the BZ powerPBZ/P0versusnw itha＊=0.542(solid)anda＊=0.502(dash)图3 BZ功率,PBZ/P0随n变化的曲线,其中a＊ =0.542(实线),a＊ =0.502(虚线)

Based on these discussions mentioned above,Q PO components (several Hz) in some observationsofXRBs[25,26]. W hat mechanism s induce these phenomena is also an interesting problem.

Summarizing the above discussion, the observations involved HFQ PO s are very complicated, behaving multiple features, so a variety of mechanism s and models need to be invoked to fit the HFQ PO s in XRBs.we find that the HFQ PO s and state transition in XRBs are relative w ith medium shell in XRBs.So,we think that the occurring of HFQ PO smaybe not only dependent on the interacting between accretion disk and central compact object,but also dependent on the astrophysical environmentin XRBs.

5 D iscussion

In this paper,based on the non-axisymmetric CEBZ M C model,we explain how to produce 3∶2∶1 ratio of HFQ PO s and discuss the astrophysical environment by virtue of analysing the correlation between HFQ PO s,jet and state transition in XTE J1550-564.

In fact, Itis well known thatthe three HFQ PO s in XTE J1550-564 not always together occur.In one duration,3∶2 HFQ PO pairs occur,but in another duration, single HFQ PO occurs[10,11]. Follow ing ourdiscussions in this paper, these phenomena indicate that the distribution of medium shell,such as the place,the height,the thickness,and so on,may be changing in different duration. That means the physical surrounding in XTE J1550-564 is very complicated.

In addition,it is shown there exists positive correlation between HFQ PO s and low frequency

[1] M organ E H,Rem illard R A,Greiner J.RXTE observations of Q PO s in the black hole candidate GRS 1915+105[J].ApJ,1997,482:993-1 010.

[2] van der Klis M.M illisecond oscillations in X-ray binaries[J].ARAA,2000,38:717-760.

[3] Rem illard R A,M organ E H,M cClintock JE,et al.RXTE observations of 0.1～300 Hz quasi-periodic oscillations in the m icroquasar GRO J1655-40[J].ApJ,1999,522:397-412.

[4] Strohmayer T E.D iscovery of a 450 Hz quasi-periodic oscillation from the m icroquasar GRO J1655-40 w ith the Rossi X-ray t im ing explorer[J].ApJ,2001,552:L 49-L 53.

[5] Homan J,M iller J M,W ijnands R,et al.H igh-and low-frequency quasi-periodic oscillations in the X-ray light curves of the black hole transient H1743-322[J].ApJ,2005,623:383-391.

[6] Strohmayer T E.D iscovery of asecond highfrequency quasi-periodic oscillation from the m icroquasar GRS 1915+105[J].ApJ,2001,554:L 169-L 172.

[7] M cClintock J E,Rem illard R A.Black hole binaries[M].Cambridge:Cambridge U niv Press,2006:157-213.

[8] Homan J,W ijnands R,van der Klis M,et al.Correlated X-ray spectral and t im ing behavior of the black hole candidateXTE J1550-564: a new interpretation of black hole states[J].ApJS,2001,132:377-402.

[9] M iller J M,W ijnands R,Homan J,et al.H ighfrequency quasi-periodic oscillationsin the 2000 outburst of the galactic m icroquasar XTE J1550-564[J].ApJ,2001,563:928-933.

[10] Rem illard R A,Sobczak G J,M uno M P,et al.Characterizing the quasi-periodic oscillationbehavior of the X-ray nova XTE J1550-564[J].2002,ApJ,564:962-973.

[11] Rem illard R A,M uno M P,M cClintock J E,et al.Evidence for harmonic relationships in the highfrequency quasi-periodic oscillations of XTE J1550-564 and GRO J1655-40[J].ApJ,2002,580:1 030-1 042.

[12] Rem illard R A,M cClintock J E.X-ray properties of black-hole binaries[J].ARAA,2006,44:49-92.

[13] W ang D X,M a R Y,L eiW H,et al.A n analytic model of a rotating hotspot and kilohertz quasiperiodic oscillations in X-ray binaries[J].MNRA S,2003,344:473-480.

[14] W ang D X,Ye Y C,Yao G Z,et al.A n analytic model of a rotating hotspot and kilohertz quasiperiodic oscillations in X-ray binaries[J].MNRA S,2005,359:36-42.

[15] Kadom tsev B B.Hydromagnetic stability of a plasma[J].Rev Plasma Phys,1966,2:153-170.

[16] Bateman G.M HD Instabilities[M].Cambridge:The M IT Press,1978:270.

[17] W ang D X,M a R Y,L ei W H,et al.Screw instability of the magnetic field connecting a rotating black hole w ith its surrounding disk[J].ApJ,2004,601:1 031-1 037.

[18] W ang D X,Xiao K,L eiW H.Evolution characteristics of the central black hole of a magnetized accretion disc[J].MNRA S,2002,335:655-664.

[19] Fendt C.Coll imated jet magnetospheres around rotating black holes,general relativistic force-free 2D equilibrium[J].A&A,1997,319:1 025-1 035.

[20] M acdonald D,Thorne K S.Black-hole electrodynam ics - an absolute-space/universal-t ime formulation[J].MNRA S,1982,198:345-382.

[21] Corbel S,Kaare P,Jain R K,et al.X-ray states and radio em ission in the black hole candidate XTE J1550-564[J].ApJ,2001,554:43-48.

[22] Fender R P,Belloni T,Gallo E.Towards a unified model for black hole X-ray binary jets[J].MNRA S,2004,355:1 105-1 118.

[23] W ang X Y,Dai Z G,L u T.External shock model for the large-scale,relativistic X-ray jets from the m icroquasar XTE J1550-564[J].ApJ,2003,592:347-353.

[24] O rosz J A,Groot P J,van der Klis M,et al.Dynam icalevidence fora black Hole in the m icroquasar XTE J1550-564[J].ApJ,2002,568:845-861.

[25] Psaltis D,Belloni T,van der KlisM.Correlations in quasi-periodic oscillation and noise frequencies among neutron star and black hole X-ray binaries[J].ApJ,1999,520:262-270.

[26] T itarchuk L,Wood K.Onthe low and high frequency correlation in quasi-periodic oscillations among white dwarf,neutron star,and black hole binaries[J].ApJ,2002,577:L 23-L 26.

P145.8

A

1672-4321(2010)03-0046-07

黑洞双星高频准周期振荡3∶2∶1频率比的理想模型

叶永春,黄昌印,雷卫华,汪定雄
(华中科技大学物理学院,武汉430074)

在Blandford-Znajek(BZ)过程和非轴对称磁场的磁耦合(M C)过程共存模型的基础上解释了黑洞双星XTE J1550-564令人困惑的高频准周期振荡(HFQ PO)的3∶2∶1频率比.结果表明:高频准周期振荡中的两个频率可以用M C过程导致的两个旋转热斑来拟合,另外一个高频准周期振荡频率与BZ过程产生的磁热斑有关.进一步地,讨论了与黑洞双星XTE J1550-564高频准周期振荡、喷流以及态转变相关的天体物理环境.

吸积;吸积盘;黑洞物理;X射线双星;磁场;不稳定性;振荡

2010-07-29 ＊通讯作者:汪定雄(1946-),男,教授,博导,研究方向:黑洞天体物理,E-mail:dxwang@mail.hust.edu.cn

叶永春(1982-),男,博士,硕士生导师,研究方向:黑洞天体物理,E-mail:leavesspring@sina.com

国家自然科学基金资助项目(10873005)