基于压缩感知的稀疏事件检测

朱翠涛,瞿 毅

(中南民族大学电子信息工程学院,武汉430074)

基于压缩感知的稀疏事件检测

朱翠涛,瞿 毅

(中南民族大学电子信息工程学院,武汉430074)

为了提高无线传感器网络中稀疏事件的检测概率,利用压缩感知技术,提出了一种改进的下降迭代检测算法.该算法通过动态调节参数,改变迭代权值,加快了算法收敛速度.实验结果表明:在相同条件下,改进算法的成功检测概率比贝叶斯算法平均提高了13%.

压缩感知;稀疏事件检测;无线传感器网络

在大规模无线传感器网络中,由于电池耗尽、传感器节点休眠、人为或自然损坏等原因,常常有大量传感器节点处于非正常工作状态.为了维护无线传感器网络的正常运行,及时、准确地了解无线传感器网络的运行状况,是十分必要的.为此,人们做了大量的研究工作.文献[1]提出了一种改进的权值信任评估检测算法.算法规定每一个父节点为其子节点分配一个权值,子节点向父节点发送数据,对应的父节点将接收的数据与对应子节点的权值相乘相加,得到一个融合值.当发现本次的融合值与上次的值不一致时,就减小相应子节点的权值,如此循环检测.但是权值的阈值很难确定,容易造成误检.文献[2]提出一种基于心跳机制的节点亚死亡状态检测方法.采用邻居检测方法检测节点是否处于沉默期,并参考节点自测电压值与重启现象判断是否进入了亚死亡状态.但是用于判断HTO的经验值一般难以确定,需要考虑通信丢包与回电周期,影响节点工作状态的检测.文献[3]提出一种将压缩感知与贝叶斯结合的算法.用观测点采集的无线传感器网络中处于工作状态的传感器节点,根据观测得到的值,使用边际似然最大和迭代逼近方法求出超参数,以及稀疏信号的先验概率.由于稀疏信号服从多元高斯分布,通过贝叶斯定理求解稀疏信号的后验概率和概率密度函数,然后取后验估计的均值作为稀疏信号的点估计.但是用最大似然求先验概率容易造成过学习,影响稀疏信号的点估计,导致稀疏事件的检测概率减小.

为了提高检测算法的自适应能力、稳健性和检测的准确性,本文利用压缩感知技术,并提出了一种改进的下降迭代检测算法.通过动态调节参数来改变权值,加快算法的收敛速度.实验结果表明,该算法与贝叶斯检测算法相比,明显提高了稀疏事件的检测概率.

1 系统模型

系统模型如图1所示.在一定区域内,随机分布个传感器.在某时刻有K(K≪N)个传感器处于工作状态,用黑色实心圆表示.N-K个处于非正常工作状态,用空心圆表示.观测节点有M(M≪N)个,用双圆表示.处于工作状态的传感器将测到的信号发给观测节点,经观测节点处理后,将网络的工作情况发给监控中心.

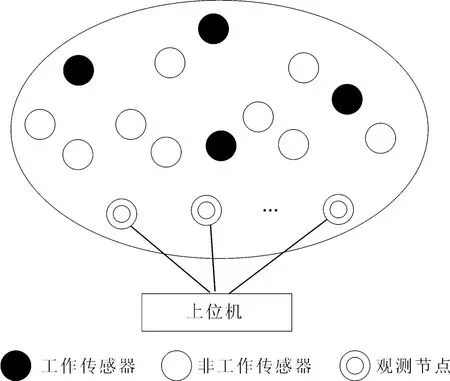
图1 系统模型Fig.1 System Model

设第m个观测节点(1≤m≤M)与第n个传感器(1≤n≤N)之间的传播距离为dm,n,α是衰减因子,信号的衰减量为(dm,n)-α.由于多径传播的影响,第m个观测节点接收的多径信号为rm,n.其包络｜rm,n｜服从瑞利分布.第m个观测节点检测到第n个传感器的信号为:

在整个无线传感器网络中,M个观测点与N个传感器节点之间的传输矩阵如下:

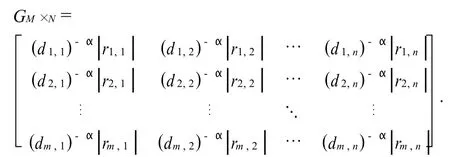
令XN×1为一个稀疏信号向量,其中每一个元素的取值为0或1.元素值为0表示传感器节点处于非工作状态,元素值为1表示传感器节点处于工作状态.所以M个观测点检测的信号表示为GM×NXN×1.设噪声为高斯噪声,均值为0,方差为σ2,用向量∈M×1表示.观测到的信号为:

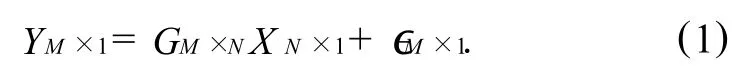
2 问题描述

在无线传感器网络中,用M个观测点检测N个传感器节点产生K事件,这三者之间关系满足:K≤M≤N.当有多个传感器节点同时给一个观测点发送信息,信息之间相互叠加,并且信号在传播过程中存在衰减.那么在这些情况的干扰下,如何使用较少的观测点仍能以较大的概率检测稀疏事件.由文献[4]可知,要用较少的观测点检测出无线传感器网络中的稀疏事件,必须存在如下关系:M≥cKlog2(N/K),其中c是一个小常数.当K减小时,cKlog2(N/K)减小,观测点M的下限值也相应减小,于是在检测过程中就可以使用更少的观测点检测稀疏事件.

因此,问题的数学模型如下:

0范数不是一个凸优化问题,一般很难求解.文献[5-6]提出,在凸优化问题中,只有1范数的解才是最接近0范数的最优解.两者的稀疏解近似等价,于是将0范数问题转化为求解1范数问题.对于式(3)求解,常用的办法就是基追踪,匹配追踪,正交匹配追踪等等.为了提高式(3)中稀疏信号的检测概率,本文在目标函数中引入权值,提出一种改进的下降迭代检测算法.因为所以将1范数转换为如下形式:

在YM×1=GM×NXN×1约束条件下,目标函数m in可以取得近似稀疏解. 现在令λM×1是一个M维的向量因子,由欧拉—拉格朗日定理得到:

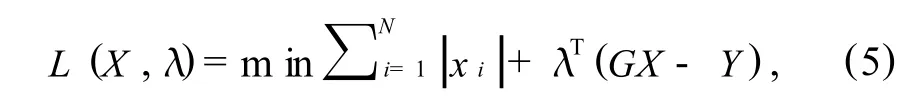
对式(5)两边求导,得:

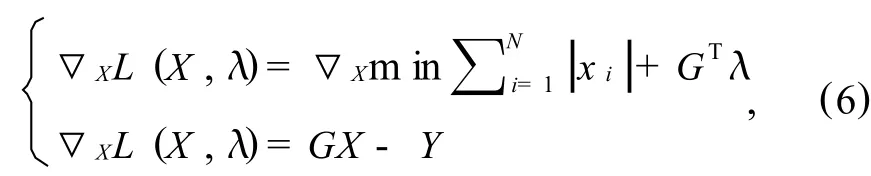
令式(6)等于零,得:

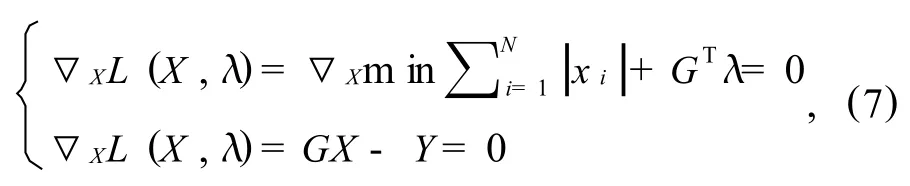
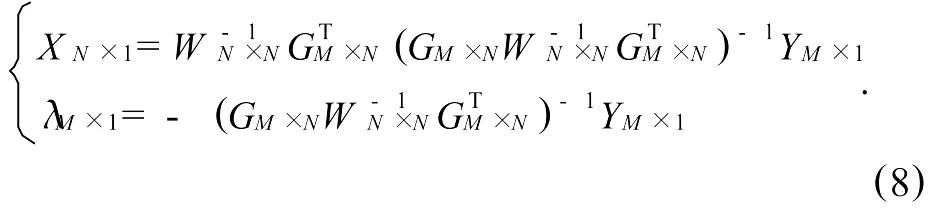
3 检测算法实现

根据以上的推导过程,得到整个检测算法的具体实现步骤如下.

(1)初始化迭代次数l(0≤l≤lmax),w(0)i=1,(i=1,2,…,n),参数α和αmin,向量XN×1;

(2)若迭代次数l大于lmax,则停止迭代,返回主程序.否则转到第3步;

(3)更新权值.对于每一个i=1,2,…,n,有

(5)将α参数缩小1 0倍,跳转到第2步继续执行.

改进的下降迭代检测算法流程如图2所示.

4 试验仿真与结果分析

利用MA TLAB 7.0软件对改进的下降迭代检测算法进行仿真.环境参数设置如下:在一个300×300m2方形区域中,随机分布128个传感器节点,其中有5个传感器节点处于工作状态,123个传感器节点处于非工作状态.并且信号在传输过程中的衰减因子为2.

在相同条件下,比较了改进的下降迭代算法与贝叶斯算法的检测概率.首先,两种算法在每一个观测点处各自完成100次仿真检测.其次,每完成一次检测,计算出检测的信号与原始信号之间的相对误差.如果相对误差值小于阈值0.05,就认为检测成功.否则认为检测失败.然后得到成功检测的次数占总次数的百分比.图3,图4分别是用20个和50个观测点比较两种算法的检测概率与观测点之间的关系.

由图3和4可以看出,当观测节点数小于12时,两种算法的检测概率基本都为0.主要原因是观测点得到的数据丢掉了较多有用信息,导致两种检测算法都不能通过观测数据恢复原始信号,不能检测到稀疏事件.随着观测点数的增多,改进的下降迭代算法与贝叶斯算法的检测概率都变大.在观测点数为50个情况下,改进的下降迭代算法的平均检测概率比贝叶斯算法提高约13%.同时可以看出,在相同的检测概率下,改进的下降迭代算法比贝叶斯算法使用更少的观测点.另外,随着观测点数的增多,改进的下降迭代算法的曲线趋于平缓,表明该算法具有较好的稳健性.

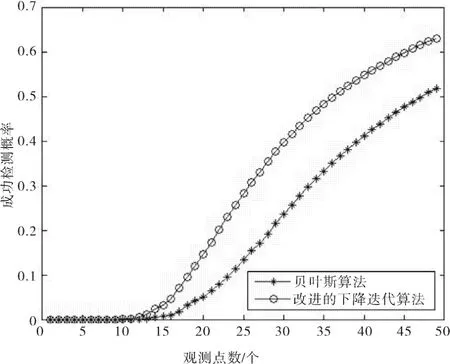
图4 50个观测点的两种算法检测概率Fig.4 50 observation ponits for two algorithm s detection probablity

5 结语

本文将压缩感知技术应用于无线传感器网络中,在其基础上提出了一种改进的下降迭代检测算法.试验结果表明,该算法与贝叶斯检测算法相比,检测概率提高了13%.目前,该算法只能检测出无线传感器网络中传感器节点的工作状态.不能够恢复工作传感器检测的实际环境信号.另外在性噪比比较小的情况下,成功检测概率会减小.因此,这些方面的改进将是下一步研究的重点.

[1] A takli IdrisM,Hu Hongbing,Chen Yu,et al.M alicious node detection in w ireless sensor networks using weighted trust evaluation[C]//ACM.The 2008 Spring S imulation M ulticonference,SanD iego:ACM Press,2008:836-843.

[2] 胡立琼,舒 坚,吴振华,等.应用于事件检测的无线传感器网络节点死活状态的研究[J].计算机科学,2009,36(9):39-43.

[3] M eng Jia,L iHusheng,Han Zhu.Sparse event detection in w ireless sensor networks using compressive sensing[C]//Barbara A Sullivan.The 43rd A nnual Conference on Information Sciences and System s.Jeff Sooknarine:Johns-Hopkins U niversity,2009: 181-185.

[4] Candes E J,Tao T.N ear-opt imal signal recovery from random projections: U niversal encoding strategies[J].IEEE T rans Inform Theory,2006,52(12):5406-5425.

[5] Bruckstein A,Donoho D L,Elad M.From sparse solutions of system s of equations to sparse modeling of signals and images[J].SI AM Review,2007,51(1):34-81.

[6] Donoho D L,EladM.Opt imally sparse representation in general(non-orthogonal)dictionaries via L 1 m in im ization[J].Proc N atl A cad Sci,2003,100(5):2197-2202.

[7] Rao B D,KreutzD K.A n affine scaling methodology for best basis selection[J]. IEEE T ransactions on Signal Processing,1999,47(1):187-200.

Sparse EventDetection Based on Compressive Sensing

Zhu Cuitao,Q u Y i
(College of Electronics and Information Engineering,South-CentralU niversity for N ationalities,W uhan 430074,China)

In the w ireless sensor networks,to improve detection probability,a modified descent iterative algorithm is proposed based on compressive sensing,which could adjust the parameter dynam ically,and then change the value of weight.A s a result,the speed of algorithm′s convergence can be accelerated.Exper imental results show that,other things being equal,comparing w ith the bayesion algorithm,the detection probability of modified descent iterative algorithm is improved averagely by 13%.

compressive sensing;sparse event detection;w ireless sensor networks

TP393.17

A

1672-4321(2011)01-0080-04

2010-12-10

朱翠涛(1967-),男,博士,教授,研究方向:认知无线电网络及分布式计算,E-mail:zhucuitao@gmail.com

国家自然科学基金资助项目(61072075)