体育统计教学中假设检验的教学方法建议

曹远红

（湖南师范大学 体育学院，湖南 长沙 410012）

体育统计教学中假设检验的教学方法建议

曹远红

（湖南师范大学 体育学院，湖南 长沙 410012）

在体育统计的教学实践中发现，学生对假设检验的方法和原理难以理解和掌握。建议用区间估计和假设检验的内容合并起来进行假设检验教学；从区间估计的角度论述了假设检验中的小概率事件，进而对假设检验中原假设的建立、统计量的计算等问题进行了论述。

体育统计；区间估计；假设检验

体育统计经过几代体育统计工作者的努力,现已成为体育科学体系中的重要组成部分,是体育科学研究和体育事业发展不可或缺的重要力量。体育统计在我国正式设立为一门体育专业基础课程,迄今已30年。[1]假设检验是体育统计教学中的重要内容，也是体育科研中经常运用的重要的统计分析方法。虽然我们现在借助计算机软件能够较快捷地进行假设检验，但是计算机软件的运用必须是在正确的数理统计原理的基础上进行的。已有的研究表明,大学本科生、硕士研究生和博士研究生在其撰写的毕业论文中,均不同程度地存在着体育统计误用的情况。[2]因此，熟练掌握和运用假设检验的原理和方法对从事体育科研工作有着重要的实践意义。

区间估计和假设检验是统计推断中的重要内容，是两个不同的统计概念，但它们又有着密切的联系。在某种意义下是同一问题的不同表达方式。这两种统计推断方法都是通过对具体事物的随机抽样所得到的样本数据，用数理统计的方法进行统计分析并做出判断的。因此，从区间估计和假设检验的双重角度进行教学，有助于学生正确掌握和理解假设检验的原理和方法。

一、假设检验基本思想和原理的论述

假设检验的基本思想和原理普遍认为是带有概率性质的反证法，在目前常用的《体育统计学》教材中对假设检验基本思想和原理都有论述，但容易让学生产生一种误解：即“假设检验是运用小概率事件原理的反证法”，学生对假设检验中到底什么是小概率事件认识不清。特别是教材中“如果发生了，则应拒绝原假设”这样的话更不能准确理解，学生容易陷入“假设检验中到底发生了什么事”这样的疑团中。准确地说，假设检验的推理有两个特点：第一，用了反证法的思想。为了判断一个“断言”是否成立，先假设该“断言”成立，然后分析由此会产生什么结果，如果导致了一个不合理的现象出现，就表明这个“断言”不成立。通常，我们称假设“断言”成立为原假设，记为H0，与之对立的称为备选假设，记为H1；第二，用了小概率原则，前面所说的“不合理”现象并非逻辑上的错误，而是违背了称之为小概率事件原理：小概率事件在一次试验中是几乎不可能发生的。[3]

小概率事件的原理实际上包含了这样的意思：“如果某事件发生的概率很小，在一次实验中，我们是可以忽略它的，也即在一次实验中不会发生。如果某事件在一次实验中就发生了，我们就没有足够的理由认为这个事件是小概率事件，也就不能忽略”。理解小概率事件原理的应用，关键是要明确假设检验中到底什么是小概率事件。

二、假设检验的实质

体育统计虽说是一门应用性体育学科,但也是以概率论和数理统计为理论基础的很精深的学问，必须在掌握和理解一定的数理统计原理的基础上，才能正确地应用在体育科研当中。在体育统计的教学中实践中，“教师教得卖力,学生学得吃力,体育统计用起来费力”，可以说是其真实写照。作为体育统计课程的教师应该根据体育专业学生的实际情况，认真钻研教法，把复杂的统计问题简单化，让学生容易接受和理解。下面以常见的“差异性”检验为例，从区间估计和假设检验的本身两个角度进行深入理解假设检验的原理和方法。

（一）从区间估计的角度理解假设检验

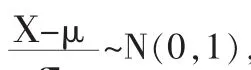
（二）从差异的来源角度理解假设检验

在假设检验中通常是对样本平均数（率）与总体平均数（率）的差异或者两样本之间平均数（率）的差异进行检验。差异的来源通常有：过失误差、条件误差、抽样误差、随机误差，而过失误差我们认为可以避免，随机误差一般我们不予考虑，主要是考虑条件误差和抽样误差。抽样误差是不可避免的，但样本仍是来自同一总体，所以这种差异没有本质区别；条件误差是实验因素或观察条件的改变而造成的差异，此时样本可能会来自不同质的总体，其差别是本质性的差别，假设检验就是帮助人们去区分差异是由抽样误差还是条件误差造成的一种科学方法。[5]下面以实例来说明假设检验。

例：由全国青少儿体质调查资料已知10岁男孩身高的平均数为135.3厘米。随机抽测海淀区120名10岁男孩的平均身高数为137.2厘米，标准差为5.9厘米，问海淀区10岁男孩身高与全国10岁男孩身高之间有无显著性差异？（α=0.05）

由题可知，μ0=135.3，X軍=137.2，差异为：X軍-μ0，造成它们之间的差异有两种原因，即抽样误差、条件误差，如果是抽样误差造成的，则说明这个差异没有本质区别，也即差异无显著性，如果是条件误差引起的，则差异具有本质性，也即差异具有显著性。题中给出的α=0.05，即说明抽样误差的概率如果小于或等于5%，那么抽样误差可以忽略，就认为这个差异是由于条件误差引起的，如果抽样误差的概率大于5%就没有足够的理由认为这个差异是由条件误差引起的。抽样误差概率的大小是可以通过计算统计量并根据统计量所对应的概率进行判断的。此题的解法如下：

解：（1）建立原假设 H0：μ=μ0=135.3

原假设怎么建立呢？根据奈曼与皮尔逊（Neyman＆Pearson）原则，我们在假设检验中更倾向于拒绝H0，而不是接受H0。换句话说，如果我们拒绝了H0，我们就有1－α把握相信为H0伪；但若接受H0，我们只能说没有足够的证据证明H0为伪。[6]为了便于学生理解，本人认为可以说原假设一般是无显著性差异或者肯定性假设。题中原假设的意思是：海淀区10岁男孩平均身高等于全国10岁男孩的身高，也即题中平均身高的差异可能是由抽样误差的引起的，此差异无显著性，抽样误差的概率大于5%。

（2）计算统计量Z值（也是我们常说的U值）：

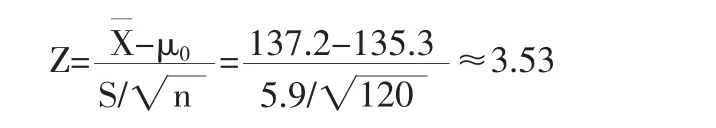
（3）α=0.05，则|Zα/2|=1.96

（4）判断结果：Z=3.53>1.96，则 P<0.05，拒绝 H0，认为海淀区10岁男孩的身高与全国10岁男孩的身高之间的差异有显著性。

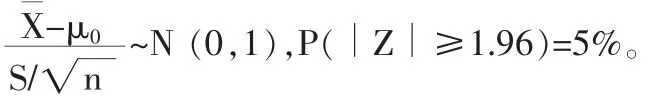
总之，不管是单侧还是双侧检验，首先是要要理解在原假设成立的基础上，样本平均数的分布形式及小概率区间，若落入小概率区间，则发生了小概率事件，就依据小概率事件原理拒绝原假设，否则只能接受原假设。

[1]权德庆，等，体育统计学科现状与发展趋势[J].西安体育学院学报，2008，(1).

[2]李健，祁国鹰，等.从体育统计误用透视高校体育统计教育[J].体育科技，2009，(1).

[3]叶鹰，等.概率论与数理统计（第二版）[M].武汉：华中科技大学出版社，2004，(9).

[4]费宇.应用数理统计[M].北京：科学出版社，2007，(8).

[5]祁国鹰，等.体育统计简明教程[M].北京：北京体育大学出版社，2004,(4).

[6]康铁祥.深入理解假设检验原理[J].统计教育，2001,(1).