排队论在设定产品维修服务人员中的应用

刘 冬，朱 玲，赫连志巍*

(1燕山大学经济管理学院，河北秦皇岛，066000;2中国人民大学)

随着科学技术的发展与经济水平的提高，顾客的消费水平随之提高，消费范围也更宽阔，于是，对于产品维修服务的需求也与日俱增。由于顾客到达的随机性与产品销售的不确定性，让顾客进行排队等待是难以避免的。因此，企业对产品维修服务系统进行深入研究并优化是非常必要的。

产品的维修服务是企业管理中的重要环节，它极大地影响着顾客对企业产品的满意度和信赖程度［1］。从实践看，维修服务人员设置得过少会增加顾客的等待成本，顾客的满意度下降;但是设置过多会增加服务成本，造成不必要的资源浪费。所以，做好维修服务人员的配置将使服务系统成本最小化，也有助于提高企业的售后服务效率。

1 产品维修服务系统模型建立的假设

顾客按先后顺序到达维修服务系统(提出服务要求)，系统满足统计平衡状态，即同一时刻有一个顾客到达或离开产品维修服系统。

(1)每天需要维修服务的顾客数量不能确定，每个顾客到达产品维修服务系统的时间分布服从Poisson分布［2］，具有一定的平稳性、普通性，且任意两个不相交的区间顾客到达情况相互独立。

(2)每个产品维修服务人员的服务时间服从负指数分布［3］。

(3)维修的服务规则为先到先服务。

(4)顾客到达后均可进入系统，并自动排成队列，进行等待。

2 产品维修服务系统排队模型及其主要评价指标分析

2．1 产品维修服务排队系统模型的建立

顾客来到产品维修服务机构想要得到维修服务，有时可以立刻得到维修服务，有时等待的顾客比较多则不能立刻得到维修服务，必须等待，顾客自动排成队列，等到接受服务后离开产品维修服务系统。它的一般形式为X/Y/Z/A/B/C［4］，其中X表示顾客相继到达时间间隔的分布;Y表示服务时间的分布;Z表示维修服务人员的数量;A表示系统的容量，即可容纳的最多排队顾客数;B表示顾客源的数目;C表示服务规则。

图1为单队列单维修服务人员的排队系统，即只有一个产品维修服务人员的系统，其排队服务模型为M/M/1/∞/∞。这种服务模型适用于中小型生产企业的售后服务模型，且其市场是较为集中的小型区域市场。图2为多队列多维修服务人员的售后服务模型，是指顾客自动排成s列等待队列，且不允许插队，有s名维修服务人员对顾客进行服务，其排队模型为s列并联的M/M/1/∞/∞。该模型适用于大型单品种产品的售后服务系统，并且其面向的市场为顾客源集中的中小型城市或顾客源较为分散的区域市场。图3为单队列多维修服务人员的系统，即顾客排成一队进行等待，选择空闲的维修人员接受维修服务。其排对模型为M/M/s/∞/∞，一般应用于顾客源集中的大城市市场［5］。

图1 单队列单维修服务人员排队系统

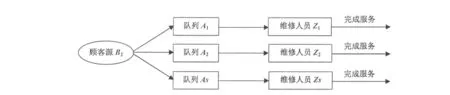
图2 多队列多维修服务人员排队系统

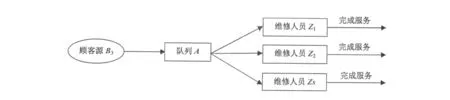
图3 单队列多维修服务人员排队系统

2．2 产品维修服务的主要评价指标分析

(1)顾客到达产品维修服务系统的平均数λ:单位时间内需要接受产品维修服务的顾客人数。λ值的高低直接受企业产品质量好坏与使用寿命长短的影响，提高产品的质量和耐用度将会降低顾客的维修人数。

(2)产品维修服务员工单位时间内的平均服务效率μ:单位时间内产品维修服务人员所能维修的产品数量。通过对员工的激励、技术培训以及规范化管理可以提高其服务效率。

(3)产品维修服务的服务强度ρ:产品维修服务人员的工作繁忙程度。ρ=λ/μ如果ρ＞1则维修人员在正常的上班时间内工作强度大，顾客等待很长的时间也可能得不到需要的服务;如果0﹤ρ﹤1则维修人员可以在工作时间完成任务，而且配置比较合理。

(4)产品维修服务人员的空闲概率p0:产品维修人员没有顾客，处于空闲的概率。

(5)顾客的平均队长L:在稳定的状态下，正在接受服务和等待服务的顾客数的均值。

(6)顾客的平均排队长Lq:在稳定的状态下，正在等待服务的顾客数的均值。

(7)顾客的平均(逗留)时间W:顾客在等待接受服务和接受服务的时间的总和的平均值。

(8)顾客的平均等待时间Wq:顾客在等待接受服务的时间的平均值。企业可以根据顾客的平均等待时间的长短来衡量企业的维修服务质量的高低和是否需要改进。

由于图1的单队列单维修服务人员的排队系统为图2系统和图3系统的特例，而图2系统在以上指标中，除给定指标外，其它可计算的指标数值均大于图3系统的指标，所以图3的单队列多维修服务人员的排队系统更具典型性，在此以图3的单队列多维修服务人员的M/M/s/∞/∞排队模型进行研究。

多服务台的M/M/s/∞/∞排队模型具有平稳分布的特性，顾客单个到达产品维修服务系统，其概率为pn=p{N=n}(n=0，1，2，…，i)。系统到达平稳状态后，可得到式(1):

式(1)表示单位时间内进入维修服务处的顾客的到达率是相等的，都为λ。

式(2)表示当顾客s的人数小于或等于维修服务人员的个数时，维修服务人员的服务效率为nμ，当顾客的人数多于维修服务人员的时候，服务人员的服务效率则一直保持不变，是全部维修服务人员工作的服务效率，为sμ。这时维修服务系统到达了满负荷率，顾客需要等待。由此可得式(3):

所以，维修服务人员空闲的概率为:

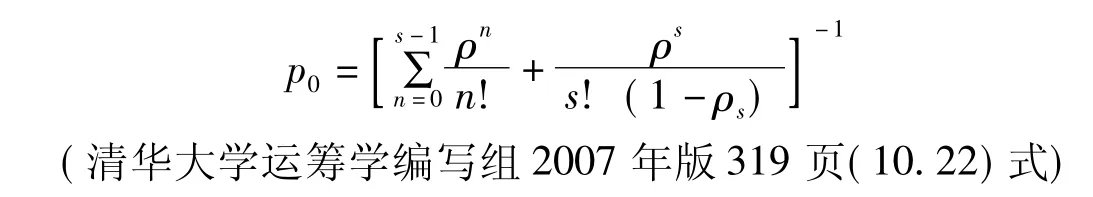
顾客的平均队长为:

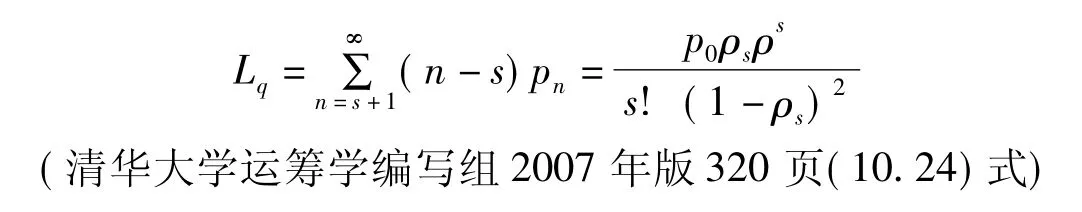
顾客的排队长为:

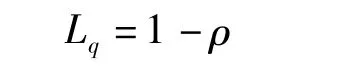
顾客的平均等待时间为:

这些指标最终的决定因素在于对顾客平均到达率λ的预测和维修服务人员的服务效率μ和维修服务人员s的设定与管理［6～8］，如激励政策、专业培训、制度建设等。企业可以将需要服务的顾客等待排队长与顾客平均等待时间这些定量指标，在达到行业的一般性要求之后，结合企业的情况调整维修服务人员数量。

3 产品维修服务系统的优化

产品维修服务系统的优化目的在于使顾客等待的时间变短，提高顾客满意度，同时降低企业的总成本，即企业维修的服务成本(人力成本和机器的损耗成本)与顾客的等待成本之合。可以通过合理配置维修服务人员的数量和提高产品维修服务人员的服务能力的方法来实现。

3．1 M/M/s/∞/∞的单队列多维修服务人员的人数S的优化

单队列多维修服务人员的M/M/s/∞/∞模型适用于大型生产企业，顾客源多，需要多个维修服务人员来保证产品维修的高时效，减少接受维修服务的顾客的等待时间，根据企业预测的顾客的平均到达率λ和根据企业情况设定维修服务率μ确定最优的产品维修服务人数s，使得产品维修服务系统效用最高。

取目标函数Cz为单位时间内系统的维修服务成本与顾客在维修服务系统中逗留成本之合的平均值，则有式(4):

其中C1为单位时间内企业维修服务人员服务1个顾客所要花费的服务成本，包括了机器的损耗费用和人工成本。C2为每个顾客在系统中逗留单位时间的成本，L为顾客的队长。

式(4)中，因为s是产品维修服务员工的数量，所以s只能取整数，则Cz(s)是离散型函数，为了取到最小的Cz(s)，以求得最优的s*，可采用边际分析法，得到式(5):

将Cz=C1s+C2L代入式(5)，可以得到两个不等式:

混凝土衬砌初凝后可拆模，拆模时应先以坚硬物敲击背面，待模板松动后再考虑进行拆膜。拆模完工后的6～18 h内，应及时养护，养护期宜为14～28 d。

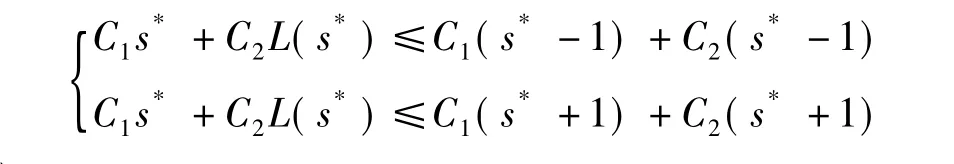
化简后可以得到式(6):

依次求当s=1，2，3，…，i时的值，并计算相邻的2个L值的差，C1/C2因为系数是一个已知数，根据不等式(6)即可确定最优的s*。

一个手机维修企业处于顾客源集中的城市，每天要求进行维修的顾客按照最简单流到达。平均每天进行维修的数量为45(人/天)，平均服务率为25(人/天)，维修服务时间服从负指数分布，C1=6(元)，C2=3(元)。求最优维修服务人员数量使得系统的总费用最小。

解:λ=45(人/天) μ=25(人/天) ρ=λ/μ=1．8

按M/M/s/∞ /∞计算p0与L(s)等。

表1 产品维修服务指数表

由于系数=2，落C1/C2在区间(0．31～6．96)之间，所以s*=3，即当设3个产品维修服务人员时可使总费用Z最小，最小值为

Z(s*)=Z(3)=24．39(元)

3．2 提高产品维修人员服务率的途径

要降低产品维修服务系统的总成本，不仅要降低企业的服务成本，更要降低单位时间内顾客的等待成本，其关键指标L(顾客单位时间内等待的队长)主要受维修服务效率的影响。通过对产品维修服务系统投入更多的资源来实现服务效率的提高。主要从提高产品维修服务人员的技能，改进对维修服务人员的管理和购买先进的维修仪器或对维修系统进行升级这3个方面提高维修服务效率，降低顾客等待成本。

通过对产品维修人员进行培训，提高其技术能力;通过改善管理，实现维修服务的标准化。对技术提高、管理改善、设备投资等3方面的资源投入分别用k′，m′，g′表示，而原来的资源投入分别为k，m，g。另外，企业采取的资源投入对服务率μ的影响比重分别设为x%，y%，z%。于是，服务效率变化的权重为:

由此得到新的服务效率为式(7):

由式(7)可知，通过对产品维修服务率的改进，将会极大地提高产品维修服务系统的服务效率，减少顾客等待的时间，降低顾客的等待成本，优化产品维修服务系统。

4 结 论

本次研究运用排队论的方法对产品的维修服务成本和效率进行了定量分析，通过对产品维修系统服务效率改进和对维修服务系统的优化，为企业选择最优服务系统提供决策依据，使企业能够为顾客提供高效的服务，并使产品维修服务系统的人力成本最小化，减少顾客的等待时间，为顾客创造服务价值，有助于培育顾客对企业产品维修服务的满意度和对企业产品的忠诚度。同时，为提高企业的服务水平，提供可以改进的路径，帮助企业制定针对性的产品维修服务对策。

［1］孙霞林，曾华，熊德之，等．基于排队的服务系统的最小成本［J］．武汉工程大学学报，2008，30(1):125-126．

［2］胡运权，郭耀煌．运筹学教程［M］．第2版．北京:清华大学出版社，2003．

［3］浙江大学．概率论与数理统计［M］．第三版．北京:高等教育出版社，2000．

［4］王新田，尹树华，李江红，等．维修员工数量配置的优化模型［J］．电子设计工程，2010，18(5):12-13，18．

［5］潘全如，朱翼隽．排队论在收费站设计与管理中的应用［J］．运筹学学报，2009，13(3):95-102．

［6］叶宗文．维修行业中排队模型的应用［J］．四川兵工学报，2009，30(10):65-68．

［7］于由．服务营销中的排队问题分析［J］．华东经济管理，2000，14(3):28-30．

［8］廖业红．运筹学排队论在客户服务中的应用与辅助决策［J］．商场现代化，2006(32):20-21．