量子棒中磁极化子的回旋共振特性和光学声子平均数

韩 超，李海峰，徐华伟*，额尔敦朝鲁

(1河北科技师范学院理化学院，河北秦皇岛，066004;2秦皇岛市广播电视大学)

由于量子棒在材料裁剪方面的自由度和在生物标记［1］及光电器件［2］中有非常广泛的应用，因此，近年来，量子棒性质的研究更为引人注目。Hu等［3］用半经验赝势方法计算了CdSe量子棒的电子态;Zhang等［4，5］在有效质量包络函数理论的框架下研究了CdSe量子棒的线偏振等的光学性质;Li等［6，7］采用赝势方法分别计算了考虑自旋与轨道耦合、电子-空穴屏蔽库仑相互作用下量子棒的高激发能和不同材料的量子棒中电子的结构。不难看出，上述工作均未涉及声子效应。然而，由于大多数的纳米结构是离子晶体或极性材料，电子-声子耦合强烈的影响着它们的物理性质［8］，因此，近年来，量子棒中电子-声子相互作用的问题也逐渐引起人们的重视。Comas等［9］用连续介质理论分析了半导体量子棒中表面极化子的光学声子的性质，并将计算出来的结果与球形量子点和准球形量子点进行了比较;最近，Wang等［10］研究了量子棒中弱耦合极化子的基态能量;巴燕燕等［11］研究了在非均匀抛物限制势下量子棒中弱耦合杂质束缚极化子的性质。笔者基于Huybrechts线性组合算符法，采用Lee-Low-Pines幺正变换和变分技术研究了磁场中量子棒内抛物限制势下电子-体纵光学声子强耦合磁极化子基态的回旋共振特性。

1 哈密顿量与变分计算

设量子棒中电子在x－y平面内和z方向上被不同的抛物势限制，并与离子晶体或极性半导体的体纵光学(Longitudinal Optical，LO)声子场相互作用，则量子棒中的电子-体纵LO声子相互作用体系的哈密顿量为［10，11］

其中v是晶体的体积，α为电子－声子耦合强度，ε∞和ε0分别是高频和静态介电常数。

首先，引入Huybrechts线性组合算符［12］

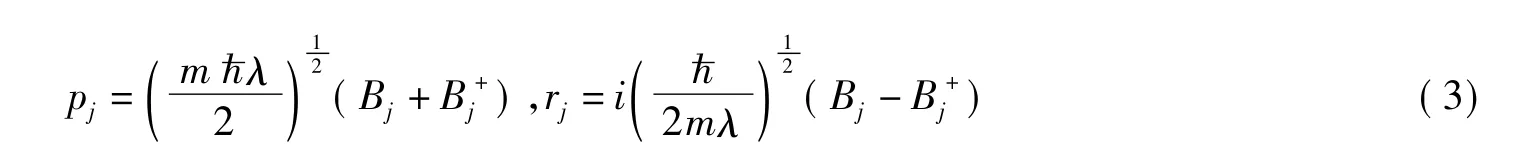
其中，j=x，y，z;λ为变分参量，表示磁极化子的振动频率。为了研究量子棒中磁极化子的基态回旋共振特性，讨论变分函数的期待值

及变分极值问题。式中

是 LLP 幺正变换［13］，其中是变分参数，

是绝对零度(0 K)下体系的基态尝试波函数。其中，|φ(z)〉为电子z方向的波函数，满足〈φ(z)|φ(z)〉=1，|0〉b为零声子态，|0〉B为极化子基态。

将(1) ～(3)式和(5)，(6)式代入(4)式，可得

其中ωc=eB/mc为磁场的回旋频率。计算和λ的变分极值可以确定磁极化子的回旋共振频率λ，再利用上述变分参数还可进一步求得体系的声子平均数为

其中

为磁极化子的声子平均数。

2 结果与讨论

为更清楚、直观地表明量子棒中强耦合磁极化子的基态回旋共振频率λ和声子平均数与量子棒的受限强度ω‖，纵横比e′，磁场的回旋频率ωc和电子－声子耦合强度α有关，笔者在此给出了数值计算结果，如图1～图6。图中以ωLO作为λ，ωc和ω‖的单位。

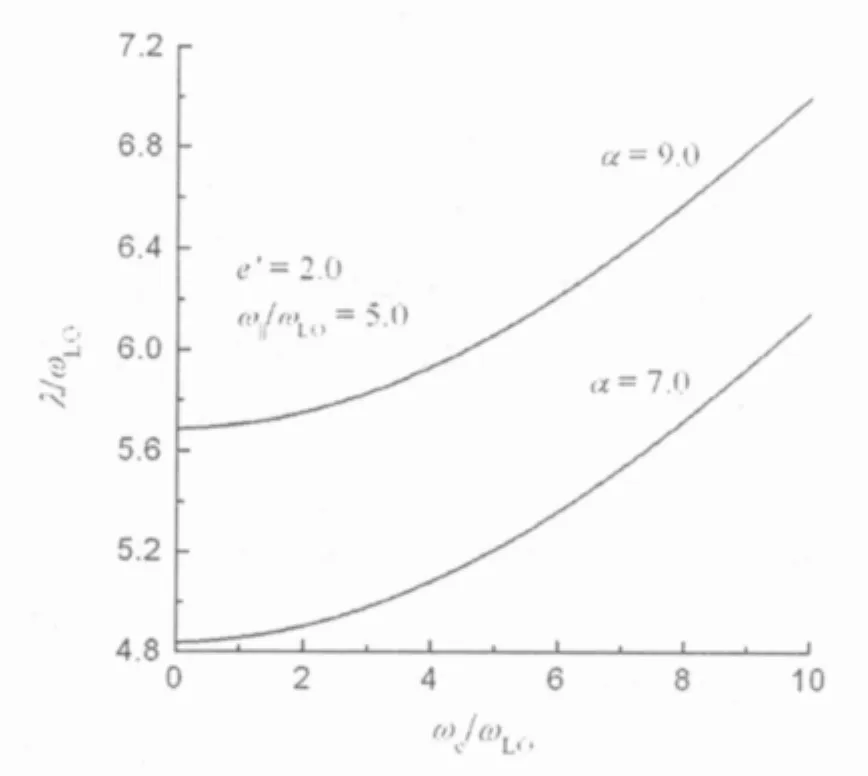
图1 频率λ在不同α下随ωc的变化

图2 频率λ在不同α下随e′的变化

图1表示量子棒中强耦合磁极化子的回旋共振频率λ在不同电子－声子耦合强度α下随磁场的回旋频率ωc的变化。由图1可看出，λ随ωc(或磁场B)的增加而增大，这表明外磁场的加入将引起晶格极化场加强，致使量子棒中电子－声子－磁场三体相互作用的能量增加，从而导致磁极化子的回旋共振振动增大。由图1还可看出，α对λ随ωc的变化产生显著影响，即λ随α的增加而增大。这是因为随α的增加，电子－声子之间相互作用能量增加，致使磁极化子的能量增大，导致磁极化子的振动频率的增大。

图2表示磁极化子的回旋共振频率λ在不同电子－声子耦合强度α下随量子棒纵横比e′的变化。由图2可看出，λ随e′的增加而减小，这是因为e′=L/(2R)(其中L为量子棒的纵向长度，R为量子棒的横向半径)，所以，随e′的增加，量子棒的纵向长度变大，以声子为媒介的电子－声子相互作用因粒子纵向运动空间的扩大而减弱，致使极化子振动频率较小。从由图2还可看出，α对λ随e′的变化也产生显著影响。λ随α的增加而增大，增加的幅度却随e′的增加而减小，因而随着e′的增加，一些不同α值对应的λ～e′曲线将出现重叠，这表明此时开始α对λ～e′曲线产生的影响可以忽略。

图3 频率λ在不同α下随ω‖的变化

图3表示磁极化子的回旋共振频率λ在不同电子－声子耦合强度α下随量子棒受限强度ω‖的变化。由图3可看出，λ随ω‖的增加而迅速增大，这是因为随着量子棒横向限定势(ω‖)的增加，以声子为媒介的电子－声子之间相互作用由于粒子运动范围缩小而增强，导致了量子棒中磁极化子的振动频率的增大。

图4表示磁极化子的声子平均数N在不同电子－声子耦合强度α下随磁场的回旋频率ωc的变化。由图4可看出随ωc的增加而增大，这表明外磁场将加强量子棒中电子－声子－磁场相互作用，使电子与更多声子相互作用，导致磁极化子的声子平均数增大。另外，α对随ωc的变化产生显著影响，当回旋频率ωc取一定值时随α的增加而增大。

图5表示磁极化子的平均声子数N在不同电子－声子耦合强度α下随量子棒纵横比e′的变化。由图5可看出随e′的增加而减小，这是因为随e′的增加，量子棒的纵向长度变大，以声子为媒介的电子－声子相互作用因粒子纵向运动空间的扩大而减弱，致使磁极化子周围声子平均数减小。由图5还可看出，α对随e′的变化产生显著影响。当量子棒纵横比e′取一定值时随α的增加而增大，但增加的幅度却随e′的增加而减小，因而随着e′的增加，一些不同α值对应的～e′曲线将出现重叠，这表明此时开始α对～e′曲线产生的影响可以忽略。

图6表示磁极化子的声子平均数N在不同电子－声子耦合强度α下随量子棒横向受限强度ω‖的变化。由图6可看出随ω‖的增加而显著增大，这是因为随着量子棒横向限定势(ω‖)的增加，以声子为媒介的电子－声子之间相互作用由于粒子运动范围缩小而增强，使电子与更多声子相互作用，导致磁极化子的声子平均数增大。由图6还可以看出，当ω‖取一定值时，电子－声子耦合强度α越大磁极化子的平均声子数越大。这是因为随着电子－声子耦合强度的增强，电子－声子之间的相互作用增强，使电子与更多的声子相互作用，导致磁极化子周围声子平均数增大。

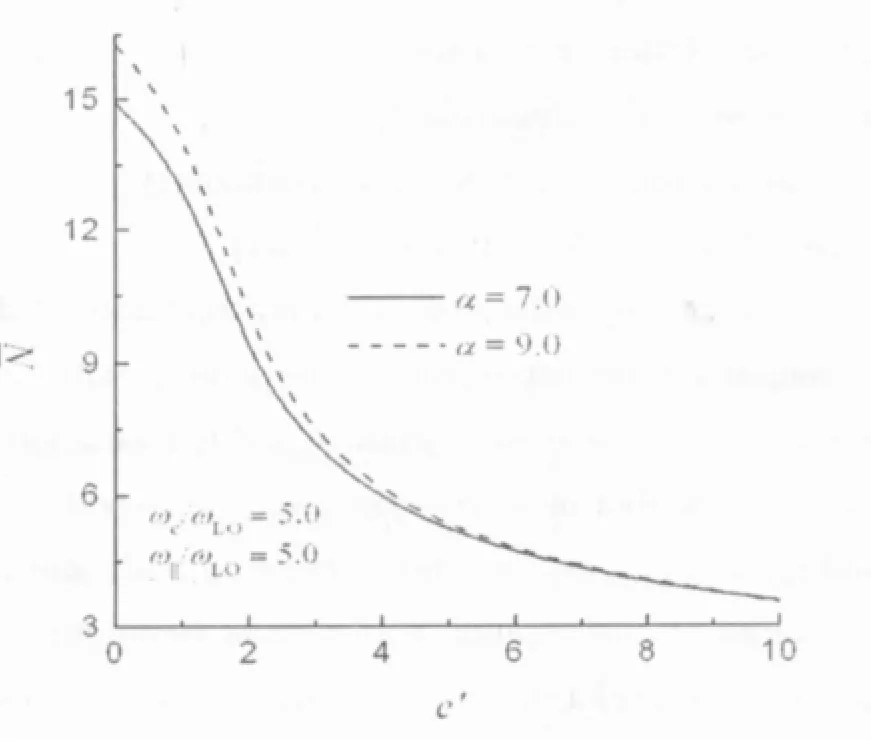
图5 声子平均数N在不同α下随e′的变化

图6 平均声子数N在不同α下随ω‖的变化

3 结 论

在有效质量近似下，基于Huybrechts的线性组合算符法和Lee-Low-Pines变分法，研究了磁场对量子棒中抛物势下强耦合磁极化子回旋共振频率和声子平均数的影响。导出了量子棒中强耦合磁极化子回旋共振频率和平均声子数与磁场的回旋频率、电子-声子耦合强度、量子棒的纵横比和受限强度的关系。结果表明:量子棒中强耦合磁极化子的声子平均数和回旋共振频率随磁场的回旋频率、电子-声子耦合强度和量子棒的受限强度的增加而增大，随量子棒纵横比的增加而减小。

［1］BRUCHEZ M，MORONNE M，GIN P，et al．Semiconductor nanocrystals as fluorescent biological labels［J］．Science，1998，281:2 013-2 016．

［2］KLIMOV V I，MIKHAILOVSKY A A，XU Su，et al．Optical gain and stimulated emission in nanocrystal quantum dots［J］．Science，2000，290:314-317．

［3］HU J T，WANG L W，LI L S，et al．Semiempirical pseudopotential calculation of electron state of CdSe quantum rods［J］．J Phys Chem B，2002，106:2447-2452．

［4］张秀文，夏建白．CdSe量子棒的线偏振光学性质［J］．半导体学报，2006，27(12):2 094-2 100．

［5］ZHANG X W，ZHU Y H，XIA J B．Optical properties and g factors of GaAs quantum rods［J］．Phys E，2006，33:376-380．

［6］LI J B，WANG L W．High energy excitations in CdSe quantum rods［J］．Nano Lett，2003，3(1):101-105．

［7］LI J B，WANG L W．Electronic structure of InP quantum rods:Difference between Wurtzite，Zinc Blende，and different orientations［J］．Nano Lett，2004，4(1):29-33．

［8］FAI CI L，TEBOUL V，MONTEIL A，et al．Polaron in a quasi 1D cylindrical quantum wire［J］．Condensed Matter Physics，2005，8(3):639-650．

［9］COMAS F，STUDART N，MARQUES G E．Optical phonons in CdSe quantum rods［J］．Solid State Commun，2004，130:477-480．

［10］王翠桃，肖景林，赵翠兰．量子棒中弱耦合极化子的基态能量［J］．半导体学报，2009，30(7):072002-1-072002-4．

［11］巴燕燕，肖景林．量子棒中弱耦合杂质束缚极化子的性质［J］．固体电子学研究与进展，2009，29(4):529-533．

［12］HUYBRECHTS J．Note on the ground-state energy of the Feynman polaron［J］．J Phys C:Solid State Phys，1976，9:L211-212．

［13］LEE T D，LOW F M，PINES D．The motion of slow electrons in a crystal［J］．Phys Rev，1953，90:297-302．