关于图形的测量

复习要求

认识了基本的几何图形，我们可以在图形的测量活动中，构建数与形之间的联系，发展测量（包括估测）、识图、作图等技能和初步的空间观念。

1.要明确线段、简单的平面图形和立体图形等空间对象的长度、面积或体积的概念，并能区分周长和面积、表面积和体积，根据计算公式正确地计算，解决实际问题。

2.在测量时，能根据实际选择恰当的测量方法，按要求画出图形，估计图形的大小。

3.掌握计量单位的实际意义及其进率，能选择适当的计量单位记录测量的结果，会进行单位之间的换算。

平面图形的测量

1.填空。

（1）一个正方形的边长是2cm，它的周长是( )cm，面积是( )cm2。

（2）平行四边形的面积40cm2，底是8cm，高是（ ）。

（3）一个平行四边形的高是8dm，面积是48dm2，与它等底等高的三角形的面积是( )cm2。

（4）用圆规画一个直径是4cm的圆时，圆规两脚之间的距离是（ ）cm，这个圆的面积是（ ）cm2，周长是( )cm。

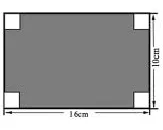
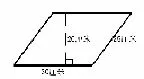
(5)如果把下图的长方形拉成一个高为5cm的平行四边形，则平行四边形的面积是（ ）cm2。

（6）一个梯形的下底是18cm。如果下底缩短8cm，就成为一个平行四边形，面积减少28cm2。原梯形的高是（ ）cm。

(9)用边长4cm的正方形硬纸板剪下一个最大的圆，这张硬纸板的损耗率是（ ）%。

(10)在下图中,圆的面积与长方形的面积相等。长方形的长是18.84cm，圆的半径是( )cm。

2.判断（在括号里正确的打“√”，错误的打“×”）。

（1）一个正方形的边长是4cm，这个正方形的周长和面积相等。 （ ）

（2）圆的直径扩大2倍,周长也扩大2倍。 （ ）

（3）长方形、正方形、圆的周长都是12.56cm，其中圆的面积最大。 （ ）

（4）下图是我国历史文化遗产《易经》中的太极图,既反映宇宙天体形状的普遍规律,又体现数与形的结合。图中阴阳两部分的面积和周长都分别相等。 (）

3.选择（在括号里填上表示正确答案的序号）。

（1）把一个平行四边形任意分割成两个梯形，这两个梯形的（ ）总是相等的。

A.面积 B.周长 C.高

（2）一个圆的半径是r，它的周长是（ ）。

A.πr B.πr+2r C.2πr

（3）一个圆的半径扩大3倍，这个圆的面积就扩大（ ）倍。A.3 B.6 C.9

（4）两个完全相同的长方形（如下图），将图①和图于阴影部分的面积相比，（ ）。

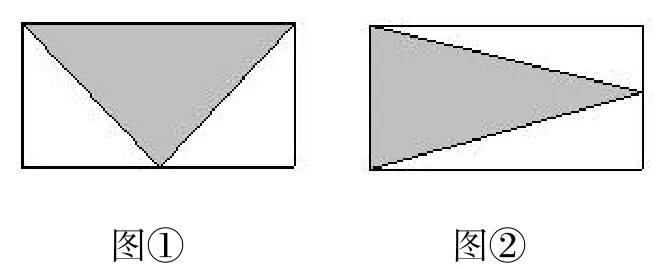
A.图①大 B.图于大 C.图①与图于相等

4.动手动脑。

（1）请你量出下列角的度数。

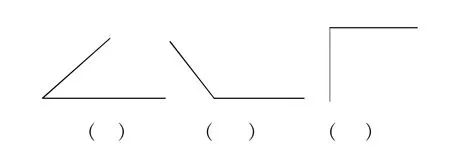
（2）画一条长4cm的线段。

（3）画一个长是4cm，宽是3cm的长方形。

（4）把下面的长方形分成两个梯形和两个三角形，且每个图形的面积相等。___

（5）在方格图中分别画出面积都是5cm2三角形、梯形各一个。（每个正方形格子的面积是1cm2）

5.先估计下面图形的周长和面积，再测量有关数据进行计算。

6.求下列图形的面积。（小方格边长是1cm）

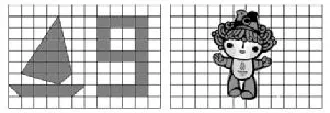
7.用16根1m长的木条靠一面墙围一块长方形菜地，怎样围面积最大？用16根小棒围一围，算一算，把结果填入下表。

?

8.一个盒子内刚好放下5杯酸奶，每瓶酸奶的瓶底半径是3 cm，盒子的长是多少？

9.计算下面各图形的面积。

（2）正方形边长1cm。

10.一个梯形的果园,上底是24m，下底是30m，高18m。如果平均每棵果树占地0.5m2，这个果园一共可以栽多少棵果树?

11.一块正方形的布料，既可以做成边长是12cm的小方巾，也可以做成边长是18cm的小方巾，都没有剩余,这块正方形布料的面积至少是多少平方厘米？

12.把一个圆形纸片沿半径分成若干个相等的扇形，然后再剪拼成一个近似的长方形。

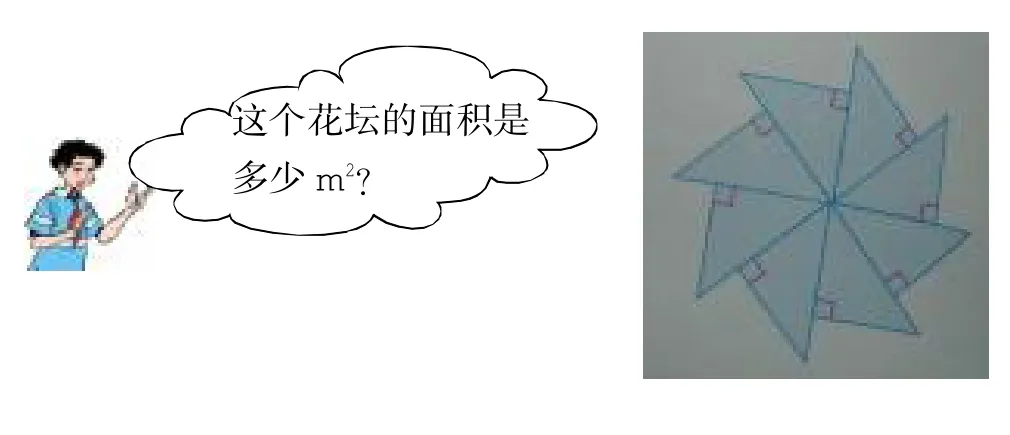
13.实验小学校园里有一个由8个等腰直角三角形组合成的花坛，每个三角形的腰长8m。

立体图形的测量

1.填空。

（1）用铁丝做一个棱长10cm的正方体框架，至少要用（ ）cm的铁丝。如果在这个正方体框架外面糊一层硬纸，至少需要（ ）cm2的硬纸。

（2）一个正方体铁块截成两个相同的长方体后，表面积增加了8dm2，原来正方体的表面积是（ ）m2。

（3）将一个长12cm、宽10cm、高6cm的长方体切成两个长方体，表面积最多增加（ ）cm2，最少增加（ ）cm2。

（4）一个圆柱体的底面周长是6.28m，高3m，它的表面积是( )m2。

(5)一个长方体木盒，从里面量得长 20cm、宽 18cm、高18cm，这个长方体木盒可存放（ ）个棱长为6cm的正方体积木。

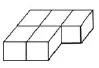
(6)右图是由五个棱长1dm的立方体组成的图形。它的表面积是（ ）dm2，体积是（ ）dm3。

(7)从里面量一个圆柱形玻璃杯，底面半径是3cm，高是10cm。在这个玻璃杯里装满水，水的体积是（ ）ml。如果将这些水倒入一个与它底面积相等的圆锥形量杯中，水高（ ）cm。

（8）一个圆柱高15dm，体积是188.4dm3，把它截成两个同样的小圆柱体后,表面积比原来增加了( )dm2。

（9）把棱长2dm的正方体木块，削成一个最大的圆柱，圆柱的体积是（ ）dm3；若削成一个最大的圆锥，那么，圆锥的体积是（ ）dm3。

（10）一个圆柱，沿一条底面直径纵切后，可以得到一个边长8cm的正方形截面，这个圆柱的体积是（ ）cm3。

（11）一种圆柱形铁皮油桶的侧面是用长3.14m（做油桶的底面周长）、宽1.4m（做油桶的高）的长方形铁皮焊接而成。那么，这个油桶的容积是（ ）m3，合（ ）升。

(12)一种高4cm的圆柱形罐头瓶的标签上写着“容量：314ml”。食品公司准备设计一种长方体的包装盒，使它能刚好装下两瓶这样的罐头，这种长方体包装盒的容积至少是（ ）cm3。

2.判断（在括号里正确的打“√”，错误的打“×”）。

(1)一个正方体的棱长之和是24cm，它的表面积是24cm2。（ ）

(2)把一个底面边长是2dm的长方体木头，截成两个小长方体，表面积增加4dm2。 （ ）

(3)一个圆柱与一个圆锥等底等高，他们的体积和为36dm3，那么圆锥体积是12dm3。 （ ）

(4)一个圆锥和一个圆柱的体积相等，底面积也相等，那么这个圆柱的高是圆锥的3倍。 （ ）

3.选择题（在括号里填上表示正确答案的序号）。

（1）有两张完全一样的长方形纸片，一张以它的长作底面周长，另一张以它的宽作底面周长，分别卷成圆柱形(接口处不重叠)，再装上底面，所得两个圆柱体的( )一定相等。

A.表面积 B.体积 C.侧面积

（2）一个圆柱体的侧面展开图是一个正方形。这个圆柱底面直径与高的比是( )。

A.1:π B.2:π C.π:1

（3）把一个圆锥的侧面展开,会得到一个( )。

A.三角形 B.扇形 C.圆形

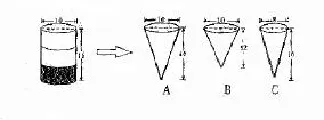
（4）圆柱内的沙子占圆柱的1/3，倒入（ ）内正好装满。

4.计算下列物体的表面积。

5.找一个长方体火柴盒，测量有关数据，算出它的内盒和外盒至少各用硬纸多少cm2（不算粘贴处）。

6.一个长方体玻璃鱼缸，长50cm，宽40cm，高30cm。

（1）玻璃每平方分米要10元，做这个鱼缸至少需要多少元钱？

（2）在鱼缸内注入40L水，水深大约是多少厘米？（玻璃厚度忽略不计）

（3）再往水里放鹅卵石、水草和鱼，水面上升了2.5cm。这些鹅卵石、水草和鱼的体积一共是多少立方厘米？

7.沙漏又称沙钟,是我国古代的一种计时仪器。一个圆锥形沙漏的底面周长是18.84dm，高是3dm，这个沙漏的体积是多少立方分米？

8.银行的工作人员通常将50枚1元的硬币摞在一起，用纸卷成圆柱的形状。

9.下面是一个圆柱侧面的展开图，计算这个圆柱的表面积和体积。(π取值为3)

10.牙膏出口处的直径为4mm，小明每次刷牙都挤出约10mm长度的牙膏。这样一来，一支牙膏可以用40次。该品牌的牙膏推出新包装，将出口处直径改为5mm。如果小明还是习惯性地挤出10mm长的牙膏使用，那么这种新包装的牙膏能用多少次?(得数保留整数)

11.航空公司规定:旅客每人可以随身携带的手提行李一件，重量不超过5kg，外形尺寸不超过：20×40×50cm。

12.将厚度为0.5cm的纸在直径为10cm的圆筒上卷成直径为20cm的卷筒纸。

关于图形的测量

■关 蓓