关于比和比例
2011-10-10齐昌建
复习要求
1.进一步理解比的意义和性质,掌握比与除法、分数的关系,会求比值和化简比。
2.进一步理解比例和比例尺的意义,掌握比例的基本性质,会解比例,能够利用比例尺求图上距离或实际距离。
3进一步理解正比例、反比例的意义,能正确判断两种相关联的量是否成比例,成什么比例。
4.能够利用比和比例的有关知识解决生活中的实际问题。
比
一、填空。
1.35 :( )=20:16=?=( )%
2.5 和它的倒数的比值是( )。
3.一个长方形的长比宽多20%,这个长方形的长和宽的最简整数比是( ):( )。
4.育才小学三年级与四年级人数比是3:4,三年级人数比四年级少,四年级比三年级多。
15.20 g盐溶解在100g水中,盐和盐水的比是( )。
16.正方形的周长和边长的比是( )。
17.甲工人5分钟做8个零件,乙工人8分钟做5个零件,他们都工作了40分钟。甲与乙所做零件个数的比是( ),乙与甲工作效率的比是( )。
5.学校把270本科技图书按2:3:4分配给低、中、高年级,低年级得到图书( )本;中年级得到图书( )本;高年级得到图书( )本。
6.甲乙两个正方形的边长比是2:3,甲乙两个正方形的周长比是( ),甲乙两个正方形的面积比是( )。
7.30 分:3时的比值是( )。
8.如果a是B的45%,那么a:B=( ):( )。
9.已知被减数与差的比是5:3,减数是100,被减数是( )。
10.甲与乙的比是6:5,甲与丙的比是3:5,乙与丙的比是( )。
11.一个直角三角形的两条直角边之和是14cm,它们的比是3:4,又知斜边长10cm,斜边上的高是( )cm。
12.甲、乙两人各走一段路,两人速度比是3:4,所用的时间比是4:5,则路程比是( )。
13.在4:8中,如果前项加上8,要使比值不变,后项应加上( )。甲、乙两班人数的比是( )。
二、判断(在括号里正确的打“√”,错误的打“×”)。
1.若圆柱体与圆锥体等底等高,则圆柱体与圆锥的体积比是3:1。 ( )
3.一个长方体的棱长和是120cm,长、宽、高的比是3:2:1,它的高是20cm。 ( )
4.小英买5个练习本用1.50元,练习本的总价与个数的比是1.50:5。 ( )
5.六(1)班有男生25人,女生24人,女生和全班人数的比是24:25。 ( )
近年来,民宿产业的发展越来越壮大。但是就目前的形势来看,却存在着一系列的问题。其一宜兴湖父镇民宿为了体现其地方特色,民宿的建筑比较陈旧,居民建设难以达到新建筑所要求的规范和水平。民宿经营者大多没有消防意识,没有进行专业的消防培训,一旦遇到险情,许多员工不知道如何进行正确的疏散、逃生。其二与民宿配套的基础设施不完善。基础设施不仅包括:水、电、交通、卫生间、空调、热水器等,也包括了其他公共设施:健身器材、停车场、活动场地等。这些配套的设施是发展民宿必不可少的一部分。民宿在经营中不仅要包含地方特色,更重要的是让游客感到舒适,这两者缺一不可。然而现在许多地方的民宿正是忽视了基础设施这一关键要素。
三、选择题。
1.a:b=c,其中a是这个比的( )。
A.前项 B.后项 C.外项
2.一个三角形的三个内角的度数比是2:3:4,这个三角形是( )。
A.锐角三角形B.直角三角形 C.钝角三角形
3.体积和高都相等的圆柱体和圆锥体,它们底面积的比是( )。
A.1:3 B.3:1 C.1:6
A.1:20 B.1:18 C.18:1
A.2:5 B.2:7 C.5:2
四、化简比。

五、求比值(求第四题各个比的比值)。
六、解决问题。
1.合唱组共有60人,男女生人数的比是5:7。这个合唱组男生、女生各有多少人?
2.一块长方形耕地,长和宽的比是5:3,又知宽比长少40米,这块耕地的面积是多少平方米?
3.修路队修一条公路,已修部分与未修部分的比是5:3,又知已修部分比未修部分长600米,这条路长多少米?
比例
一、填空。
1.根据a×b=c×d,写出一个比例式( )。
4.甲÷乙=5,乙与甲的比是( ),乙和甲成( )比例。
5.16 的约数有( ),在这些约数中,选出其中四个数,至少组成两个比例:( )
7.在一个比例式中,两个比的比值等于3,这个比例的外项为8和6,这个比例式是( )。
8.根据7.5×2=3.75×4,在能组成的比例中,比值最大的一个比例式是( )。
二、下列相关联的量成比例吗?成什么比例?
1.天数一定,每天烧煤量和烧煤总量( )比例。
2.圆的直径和面积( )比例。
3.订《现代少年报》的份数和所需要的钱数( )比例。4.被除数一定,除数和商( )比例。
5.比的后项一定,比的前项和比值( )比例。
6.全班人数一定,出勤人数和出勤率( )比例。
7.正方体一个面的面积和它的表面积( )比例。
8.在一定的时间里,做一个零件所用的时间和做零件的个数( )比例。
9.正方体体积一定,底面积和高( )比例。
10.圆锥体的高一定,圆锥的底面半径和它的体积( )比例。
11.总价一定,单价和数量( )比例。
12.圆柱的底面半径一定,圆柱的高和圆柱的体积( )比例。
13.实际距离一定,图上距离与比例尺( )比例。
14.正方形的边长和面积( )比例。
15.三角形的面积一定,底和高( )比例。
16.长方形的长一定,宽和周长( )比例。
17.圆的半径和周长( )比例。
18.总产量一定,单产量和数量( )比例。
19.做一项工程,工作效率和工作时间( )比例。
20.汽车从甲地到乙地,行车时间和速度( )比例。
三、判断(在括号里正确的打“√”,错误的打“×”)。
2.A.、B、C、D均不为零,如果A:B=C:D,那么D:C=B:A( )
3.如果ab+5=12,则a与b成反比例。( )
4.χ-y=0,且χ、y均不为零,则χ与y不成比例。( )
5.在一个比例里,两个内项的积除以两个外项的积,商是1。 ( )
6.5 、15、25、75四个数,只能组成一个比例式。 ( )7.实际距离一定,比例尺扩大10倍,图上距离也扩大10倍。 ( )
8.一个零件长10毫米,画在图上长5厘米,这幅图的比例尺是1:5。 ( )
四、选择(在括号里填上表示正确答案的序号)。
A.x<y B.x>y C.x=y
2.如果A×2=B÷3,那么A:B=( )。
A.2:3 B.3:2 C.1:6
4.下列三组中可以组成比例的是( )。
5.XY+2=K(一定)X和Y的关系是( )。
A.成正比例 B.成反比例 C.不成比例
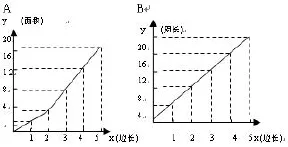
6.下面各图中都表示了x、y两种变量,( )中的两种量成正比例,( )中的两种量成反比例。

五、解比例。
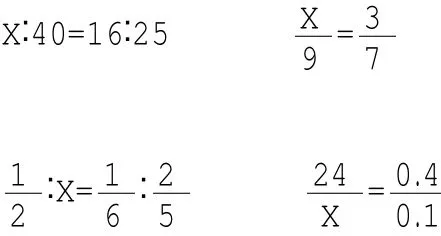
六、解决问题。
1.机床厂装配一批车床,如果每天装配50台,60天可以完成任务,如果每天装配75台,多少天可以完成任务?
2.某队安装480米的水管,前4天装了120米。照这样计算,安装完这水管还要多少天?
3.地毡厂一车间用边长4分米的水泥方砖铺地,需要5400块;如果改用边长为6分米的方砖铺地,需要多少块?
4.有一杯水,盐和水的比是1:10,再放入2克盐,新盐水重35克,求原来盐水中盐和水各有多少克?
5.在比例尺是1:4000000的地图上量得甲乙两个城市间的公路长度是15厘米,一辆时速为60千米的汽车从甲城到乙城需要多少小时?
7.王欣读一本书,已读和未读的页数之比是1:5,如果再读30页,则已读与未读的页数比是3:5。这本书共有多少页?
8.有一座闹钟,每小时慢3分钟,早上8点整对准了标准时间,当闹钟是中午12点时,标准时间是多少?
9.下面的图象表示一辆汽车在高速公路上行驶路程与耗油量的关系。

(1)这辆汽车的行驶路程与耗油量成正比例吗?为什么?
根据图象判断,行驶75千米大约耗油多少升?
(2)如果汽车在市区行驶,每50千米耗油5升,照这样的耗油量,在图上描出行驶100千米、150千米……与耗油量对应的点,再把他们按顺序连起来,行驶75千米大约耗油多少升?
10.按1:4的比画出长方形缩小后的图形。

(1)分别写出两个长方形的长的比和宽的比,并组成比例。
(2)分别写出每个长方形的长和宽的比,并组成比例。
关于比和比例
■ 齐昌建
