基于NSCT子带自适应Bayes阈值图像去噪方法

欧阳洪波， 全惠敏 ， 唐 渊 ， 曾业战

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.湖南工业大学 电气与信息工程学院，湖南 株洲 412007；3.湖南理工学院 物理与电子学院，湖南 岳阳 414000）

众所周知，在图像的成像过程中总是不可避免地受各种噪声的影响。因此，图像去噪是计算机视觉和图像处理领域中最根本和广泛的研究方向。而去噪的关键任务就是去除噪声的同时尽可能地保留原图像的边缘和细节。在变换域去噪过程中，合理地选取阈值非常重要，其直接影响到去噪效果。1992年，Donoho和Johnstone提出了小波阈值消噪法[1]，利用该方法进行图像去噪简单又有效。但Donoho给出的阈值有“过扼杀”小波系数的倾向，导致图像重构误差较大，而且小波变换往往对点奇异性比较敏感，且对边缘方向表达能力有限。为了克服小波变换的局限性，2002年M.N.Do和Martin Vetterli提出了一种多方向、多分辨率的图像表示方法，即 Contourlet变换（CT）理论[2-6]。 目前，Contourlet变换在图像去噪等领域有广泛的应用。但Contourlet变换不具有平移不变性，在进行图像处理时会引入Gibbs效应。因此，A.L.Cunha、J.P.Zhou和M.N.Do等于2006年利用非下采样塔式分解和非下采样滤波器组构造出了非下采样Contourlet变换[3]（Nonsubsampled Contourlet Transform， NSCT）。

在深入研究NSCT系数特性的基础上，采用了自适应阈值对图像分解后的NSCT系数进行硬阈值处理，该方法能自适应地调整阈值，从而有效地去除图像中的噪声和Gibbs伪影，保留图像细节，获得了更好的视觉效果和更高的PSNR值。

1 NSCT子带自适应Bayes阈值图像去噪方法

1.1 非下采样Contourlet变换

与CT类似，NSCT也是将尺度分解与方向分解分开进行。非下采样Contourlet变换分为两部分：非下采样的LP（Laplacian Pyramid）分解和非下采样的 DFB（Directional Filter Bank）分解。首先采用非下采样塔式滤波器组（Nonsubsampled Pyramid Filter bank，NSPFB）对图像进行多尺度分解，然后再采用非下采样方向滤波器组（Nonsubsampled Directional Filter Bank， NSDFB）对得到的各带通子带图像进行方向分解，从而得到不同尺度、方向的子带图像系数[7-14]。与CT不同的是，NSCT在图像的分解和重构中，取消了对图像进行上采样和下采样操作，使得非下采样Contourlet变换不仅具有多尺度、多分辨率、良好的空域、频域局部特性和多方向特性，而且具有评议不变性。NSCT变换如图1所示。

图1 NSCT变换Fig.1 Nonsubsampled contourlet transform

1.2 NSCT子带自适应Bayes阈值图像去噪的基本思想

图像去噪的一个重要任务就是去除噪声的同时尽可能地保留图像的边缘和细节。在图像去噪中，对NSCT系数（代表含噪图像经过NSCT后尺度为时，第方向的系数）的处理是关键所在，由于待去噪的图像一般包括4类信息，即图像能量、明显的边缘信息、微弱的边缘信息和噪声。对NSCT后的系数进行分析，发现图像能量主要集中在低频子带，其他的3类信息主要集中在高频子带中，图像去噪主要处理后3类信息。而后3类信息经过NSCT后，分析发现在NSCT变换域中，明显的边缘信息对应的系数在同尺度下的所有不同方向子带上都有较大的值；微弱的边缘信息所对应的系数几在同尺度内，某些方向子带上的系数大，某些方向子带上的系数小；而噪声对应于同一层内的所有不同方向子带中都有较小的值。基于对这些系数的观察，可以根据NSCT后系数的特点，不同的子带必须选择不同的阈值。子带系数的能量近视于系数系数的平方，能量越大说明轮廓信息越多，采用阈值去噪时应设置较小的阈值；能量越小说明轮廓信息越少，应设置较大的阈值；可以使用能量来调节阈值，同时，文中所采用的自适应Bayes阈值，当噪声方差增大时，Bayes阈值自动增大，当噪声方差减小时，Bayes阈值也自动减小，达到自适应去噪的目的。

1.3 NSCT子带自适应Bayes阈值

NSCT采用具有各向异性的Contourlet基来捕捉图像的方向性信息，在将小波域的BayesShrink阈值推广到NSCT域时，必须充分利用NSCT自身的这种多方向选择特性。与小波变换相比，NSCT的方向选择更加灵活，并且变换域尺度大小与原图像相同。在相同尺度、方向的情况下，NSCT系数小于小波系数。因此，文中提出带有尺度及方向信息的子带Bayes自适应阈值去噪方法。

用贝叶斯（Bayes）估计可以得到小波阈值函数的去噪方法，以下方法是将Chang在2000年提出的BayesShrink阈值估计方法[15]应用于NSCT中。BayesShrink方法是在Bayes准则下得到的，设在Bayes风险最小的条件下得到的理想阈值为：

式中：rbayes（t）为 Bayes 风险函数。

要求出上式中tˆ的解析表达式非常困难，且计算繁琐，因此一般情况下利用数值方法求出其近似解:

当 β∈[0.5， 4]时，rBayes（与 rBayes（tBayes）相差不到 5%。 而通过大量实验表明，自然图像各自带的β取值在一个很小的范围内，大致满足β∈[0.5，4]，因此tBayes的选择是合理的。从另一方面来看，该阈值的估计也符合直观理解，对固定的原始图像，当噪声方差增大时，tBayes也增大，从而可去除更多的噪声影响；而当噪声方差减小时，阈值tBayes也减小，从而保留更多的系数。

含噪图像进行NSCT的模型为

事实上，原始NSCT系数分解后的高能量区域主要对应剧烈变化的图像特征，基于这样的思想，对BayesShrink方法进行自适应改进，即将Bayes阈值公式（2）改进为：

在NSCT中选择 “maxflat”塔式滤波器进行三层分解和“dmaxflat7”进行方向滤波，方向数分别为 2、4、8时，研究发现当c为4 080时去噪效果最好。

1.4 NSCT子带自适应Bayes阈值算法流程图

1）对去噪图像进行NSCT，得到尺度为k时，第j方向的系数。

3）按式（6）计算尺度为k时，第j方向的NSCT子带自适应阈值函数。

4）进行阈值处理。文中采用硬阈值去噪得到新的非下采样 Contourlet系数。

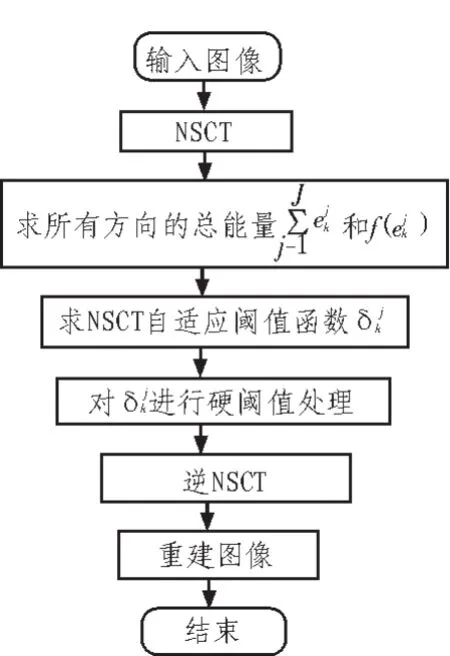
图2 算法流程图Fig.2 Flow chart of program algorithm

1.5 实验结果及分析

为验证文中所提出算法的有效性，选取加有均值为零、方 差 为 15、20、25、30 的 高 斯 白 噪 声 的 图 像 Lena、Peppers、Barbara进行实验。表1给出了文中方法和Contourlet多尺度阈值去噪、Contourlet自适应阈值去噪的PSNR值，图3为方差为25时Lena、Peppers和Barbara图像去噪后的局部结果。由表1可以看出，噪声较低时本算法比Contourlet多尺度阈值去噪、Contourlet自适应阈值去噪算法得到的PSNR值明显要高，但噪声增强后去噪效果变差；由图3可以看到，在保留图像细节的同时，该方法有效地去除了发丝状的Gibbs失真，在Lena的脸部、辣椒蒂附近、桌子脚周围处效果更突出。相对其他方法，几种图像中的Barbara去噪效果改善稍差，这与图像本身特征有关。

2 结 论

文中结合BayesShrink阈值去噪，在研究NSCT特性基础上，提出了一种基于非下采样Contourlet子带自适应Bayes图像去噪方法。利用NSCT平移不变性、多分辨率、多方向的特点，能够根据NSCT系数在各个尺度各个方向的能量，自适应调整去噪阈值。实验的结果证明，该算法在图像去噪上能获得更好的视觉效果和更高的峰值信噪比。同时需要指出的是，利用非采样Contourlet变换虽然能够取得优于基于Contourlet变换的融合效果，但是非采样Contourlet变换的算法复杂度更高、计算耗时长，因此如何提高运算速度还需要进一步的研究。

表1 不同去噪方法去噪PSNR值对比Tab.1 PSNR with different denosing methods

图3 图像 Lena、Peppers、Barbara去噪效果Fig.3 Denoising results for “Lena”image、“Peppers”image、“Barbara”image

[1]Donoho D L.De-noising by soft-thresholding[J].IEEE Trans on IT，1995，41（3）:613-627.

[2]Do M N，Contourlets V M.A directional multiresolution image representation [C]//International Conference on Image Processing，2002（1）：357-360.

[3]Cunha A L，ZHOU Jian-ping，Do N M.The nonsubsampled contourlet transform:theory，design，and application[J].IEEE Trans.on Image Processing，2006，15（10）:3089-3101.

[4]Duncan D Y，Do M N.Directional multiscale statistical modeling of images using the contourlet transform[J].IEEE Trans Image Proc，2006，15（6）:1610-1620.

[5]Do M N，Vetterli M.Pyramidal directional filter banks and curvelets[C]//Proceedings of International Conference on Image Processing，2001：158-161.

[6]YANG Fan，ZHAO Rui-zhen，HU Shao-hai.Adaptive algorithm for image denoising based on corrlation properties of contourlet coefficients[J].Acta Optica Sinica，2009，29（2）:358-361.

[7]ZHANG Qiang，GUO Bao-long.Remote sensing image fusion based on the nonsubsampled contourlet transform[J].Acta Optica Sinica，2008，28（1）:74-80.

[8]Cunha A L，Zhou J，Do M N.The nonsubsampled contourlet transform:Theory，design，and applications[J].IEEE Trans Image Proc，2006，15（10）:3089-3101.

[9]郭雷，刘坤.基于非下采样Contourlet变换的自适应图像融合算法[J].西北工业大学报，2009，27（2）:255-258.

GUO Lei，LIU Kun.ApplyingNSCT （Nonsubsampled Contourlet Transform）theory to achieving effective image fusion[J].Journal of Northwestern Polytechnical University，2009，27（2）:255-258.

[10]刘哲.基于非下采样轮廓小波变换的图像去噪[J].光电子·激光，2009，20（7）:954-958.

LIU Zhe.Image denoising via nonsubsampled wavelet-based contourlet transform[J].Journal ofOptoelectronics.Laser，2009，20（7）:954-958.

[11]何力，曲仕茹，张大奇.基于非下采样Contourlet系数尺度相关性的图像增强算法[J].西北工业大学学报，2010，28（1）:42-46.

HE Li，QU Shi-Ru，ZHANG Da-qi.Image enhancement based on inter-scale correlationsofnonsubsampled contourlet coefficients[J].JournalofNorthwesternPolytechnicalUniversity，2010，28（1）:42-46.

[12]杨鹏.一种基于非下采样Contourlet变换的子带自适应阈值去噪方法[J].西北大学报：自然科学版，2010，40（2）:251-255.

YANG Peng.Image denoising use adaptive threshold by subband in nonsubsampled Contourlet domain[J].Journal of Northwest University：Natural Science Edition，2010，40（2）:251-255.

[13]刘国金，曾孝平，刘刈.基于非下采样Contourlet变换和图正则化去噪[J].计算机应用，2010，30（6）:1556-1558.

LIU Guo-jin，ZENG Xiao-ping，LIU Yi.Image denoising based on graph regularization and nonsubsampled Contourlet transform[J].Journal of Computer Applications，2010，30（6）:1556-1558.

[14]陈建军，田逢春，邱宇，等.基于非下采样Contourlet和扩散的图像去噪[J].计算机工程，2010，36（14）:185-189.

CHEN Jian-jun，TIAN Feng-Chun，QIU Yu，elat.Image denoising based on nonsubsampled contourlet and diffusion[J].Journal of Computer Engineering，2010，36（14）:185-189.

[15]Chang S G，Yu B，Vetterlim M.Adaptive wavelet thresholding for image denoising and compression[J].IEEE Trans.Image Proc，2000，9（9）:1532-1546.