基于非负矩阵分解的图像脆弱水印算法
2011-10-09崔得龙孙国玺
崔得龙,孙国玺
(广东石油化工学院 计算机与电子信息学院,广东 茂名 525000)
数字水印作为一种有效的信息隐藏技术,随着人们对数字产品版权保护要求的不断提高得到了迅猛发展。目前,根据水印对攻击的抵抗程度不同,可将数字水印技术分为两类[1]:一是用于版权保护的鲁棒性数字水印技术;二是用于内容完整性、真实性认证的脆弱性数字水印和半脆弱性数字水印。对于第二种分类,又根据对图像认证的方式不同,可分为精确认证和内容认证[2]。精确认证把图像作为一个整体,对图像的任何篡改均是不允许的,即如果有1比特的改变,图像就不能通过认证,也称为完全认证。内容认证是指在保持图像作品内容基本不变的情况下,允许作品有一定程度的失真,而对明显改变图像内容的操作和恶意篡改则拒绝通过认证,也称为选择性认证。脆弱水印对嵌入有水印的图像的任何修改都非常敏感,因而适用于医学图像、卫星图像、遥感图像、数字地图等需要对图像进行精确认证场合。
传统的密码学数据认证技术由于存在:1)需要传输额外的数据,增加了数据量;2)加密后的乱码容易引起攻击者的注意;3)算法复杂,耗时等不足,因此不适用于图像内容完全认证。几年也有人提出将非负矩阵分解(non-negative matrix factorization,NMF)应用到脆弱性数字水印技术中[3-6],并取得了一系列的研究成果。
文中基于图像矩阵的非负特性,提出一种将水印信息嵌入图像NMF分解的系数矩阵的脆弱数字水印算法。算法首先利用用户密钥生成随机矩阵,然后将初始随机矩阵Qr分解得到正交向量集作为NMF基矩阵,二值水印信息嵌入图像NMF分解的系数矩阵。大量仿真实验结果表明了本算法的可行性,同时用户密钥提高了算法的安全性。
1 理论基础
1.1 Qr分解
Qr分解法是三种将矩阵分解的方式之一,是将原始矩阵分解成一个正交矩阵与一个上三角矩阵的积。Qr分解经常用来解线性最小二乘法问题,也是特定特征值算法的基础。
实数矩阵A的Qr分解是把矩阵A分解为:

其中,Q是正交矩阵(即QTQ=I),R是上三角矩阵,当A非奇异时因数分解结果唯一。
1.2 非负矩阵分解
定义:对一个M维的随机向量v进行N次的观测,记这些观测为 vj,j=1,2…,N,取 V=[V1,V2,…,VN],其中 Vj=vj,j=1,2,…,N,则要求存在非负的 M×L 的基矩阵 W=[W1,W2,…,WN]和 L×N 的系数矩阵 H=[H1,H2,…,HN],使得 V≈WH[7]。
通常要求 L≤min(m,N),即当 W包含随机变量的本质特征时,才能使用较少的基去描述大量的样本数据使V≈WH成立。
NMF的实现是一个优化求解的过程,Donoho证明了NMF存在唯一解的条件[8]。基本思想是合理地构造目标函数,交替地优化W和H从而得到NMF的一个局部最优解。算法的关键是目标函数的设定和迭代规则的选择,常用的目标函数和迭代规则如下:
1.3 标本采集 标本采集参照《全国临床检验操作规程》(第四版)和美国临床和实验室标准协会(Clinical and Laboratory Standards Institute,CLSI)推荐的标本采集方法[3]。
目标函数:最小化‖V-WH‖2,对于任意W,H≥0

NMF使分解后的所有分量均为非负值(纯加性),并且同时实现非线性的维数约减。纯加性和稀疏性使得对数据的描述变得方便与合理,同时还在一定程度上抑制外界变化对特征提取造成的影响。
2 脆弱NMF水印算法
2.1 水印嵌入
设 I(M1,N1)为原始图像信息,Z(M2,M2)为二值图像水印信息,则脆弱NMF水印算法嵌入过程如下:
1)利用用户密钥 Si生成初始随机矩阵 Ri(M1,N1),将 Ri进行 Qr分解得到正交向量集(M1,N1),下标 i为不同用户密钥。
2)根据 NMF 分解维数 ri,选择(M1,r1)作为图像 NMF分解基矩阵 Wi(M1,ri)。
3)对原始图像信息 I(M1,N1)进行 NMF 分解,得系数矩阵 Hi(M1,ri),分解过程中保持基矩阵 Wi(M1,ri)不更新,则系数矩阵 Hi(ri,N1)唯一。
4)缩放二值水印信息 Z(M2,N2)到 Z(ri,N1)。
6)重构Wi(M1,ri)×(ri,N1),得含水印图像I′(M1,N1)。
由水印嵌入过程可见,原始图像的所有像素都参与了水印嵌入过程,因此本算法是一种基于图像全局内容的安全水印算法。
2.2 水印检测
本算法在进行水印检测时不需要原始图像载体,属于盲水印算法。具体过程如下:
1)由用户密钥 Si生成初始随机矩阵 Ri(M1,N1),将 Ri进行 Qr分解得到正交向量集(M1,N1)。
2)根据水印嵌入时采用的NMF分解维数ri,选择(M1,ri)作为图像 NMF 分解基矩阵 Wi(M1,ri)。

水印嵌入及检查流程图如图1所示。
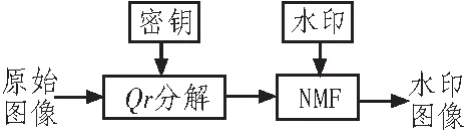
图1 图像水印嵌入流程图Fig.1 Flow chart for the watermark embedding
3 实验仿真
为了验证算法的有效性,采用512×512的灰度Lena图像作为原始图像载体,如图2(a)所示,二值图像水印信息如图2(b)所示,对原始图像载体按照2.1进行水印嵌入,其中NMF分解维数r=100,水印嵌入强度α=0.05,嵌入水印后的含水印图像如图2(c)所示,提取水印如图2(d)所示。从图2可见,无攻击下文中图像水印算法能够正确提取水印图像。
在常见图像处理攻击下的含水印图像及提取水印如图3所示,图中同时给出了提取水印图像与原始水印图像间的NC值。从实验结果可见,对含水印图像的任何攻击都会导致最终水印提取的失败。

图2 图像水印嵌入示例Fig.2 Examples of watermarking embedding
4 结 论
文中设计了一种基于NMF的脆弱图像水印算法。利用NMF的初值敏感性,由用户密钥生成NMF分解的基矩阵,并在图像NMF分解过程中保持不更新,水印信息嵌入相应NMF的系数矩阵。实验结果表明,文中算法对于含水印图像的任何轻微篡改都会导致最终水印提取的失败,是一种安全的脆弱图像水印算法。
[1]Aiello W,Bellovin S M,Blaze M,etal.Efficient,DoS Resistant,Secure Key Exchange for Internet Protocols[C]//CCS’02.Washington,DC USA,2002:18-22.
[2]Aiello W,Bellovin S M,Blaze M,et al.Just fast keying:key agreement in a hostile internet[J].ACM Transactions on Information and System Security,2004,7(2):1-30.
[3]SUN Wei,LU Wei.Blind image watermarking analysis using DWT and non-negative matrix factorization [C]//Proc of CCPR’08.Beijing:2008:1-5.
[4]孙锐,高隽.组合NMF和PCA的图像哈希方法[J].电子测量与仪器学报,2009,23(5):52-57.
SUN Rui,GAO Jun.Image hashing method via combination of NMF and PCA[J].Journal of Electronic Measurement and Instrument,2009,23(5):52-57.
[5]牛万红,潘晨.一种基于NMF的零水印算法[J].济南大学学报:自然科学版,2009,23(3):270-274.
NIU Wan-hong,PAN Chen.A non-watermarking algorithm based on NMF[J].Journal of University of Jinan:Science and Technology,2009,23(3):270-274.
[6]刘如京,杨韫饴,王玲.基于NMF和SVD相结合的Contourlet域鲁棒水印算法[J].计算机应用研究,2010,27(9):3507-3510.
[6]LIU Ru-jing,YANG Wen-yi,WANG Ling.Robust watermarking scheme based on NMF and SVD in Contourlet domain[J].Application Research of Computers,2010,27(9):3507-3510.
[7]Lee D,Seung H.Learning the parts of objects by nonnegative matrix factorization[J].Nature,1999,401(6755):788-791.
[8]Donoho D,Stodden V.When does non-negative matrix factorization give a correct decomposition into parts[C]//Adv in Neur Inform Proc Syst.Cambridge:MIT Press,2004.1141-1148.
