脑外科CT图像的综合边缘提取算法

宁 祎，高红伟

（河南工业大学 机器人研究所，河南 郑州 450001）

众所周知，脑外科手术是最复杂而危险的外科手术，只要一个微小的错误动作，就足以造成中枢神经系统的永久损害。因此若需进行脑外科手术，事先必须缜密的规划，并做好充分的准备工作，包括分毫不差地确认肿瘤位置、决定最佳的切除方式以及了解脑细胞与其他重要大脑部位的相对位置等。 随 着计算机 技术 、CT （Computed Tomography）、MRI（Magnetic Resonance Imaging）等医学影像技术的不断发展，虚拟现实技术也越来越多地应用到现代医疗领域[1]。利用计算机图像处理和数据可视化技术，根据医学影像设备提供的二维断层图像，进行人体器官的三维重建已是现代医学重要发展方向之一。图像最基本的特征是边缘，边缘是区域属性发生突变的地方，也是图像中不确定性最大的地方和图像信息最集中的地方，包含着图像的丰富信息[2－3]。图像的边缘对大脑的三维重建具有重要意义，是三维重建的重要基础，图像边缘提取的正确性和可靠性将直接影响到三维重建后的效果。CT二维图像的边缘提取作为器官三维重建的第一步，如何快速、准确地提取图像边缘信息一直受到国内外学者的关注。1959年，Julez[4]最早提出了边缘检测；1965年，Roberts[5]最早开始系统地研究边缘检测；1986年，Canny提出基于最优化算法的边缘检测算子。经过50多年的研究，已经出现了许多不同的边缘检测方法，各自有其特点和局限性，但针对脑外科CT图像的研究报道并不多。因此，本研究针对脑外科CT图像纹理复杂、细节丰富等特点，设计了一种采用图像增强、Canny算子与数学形态学相结合的综合边缘提取算法，达到了理想的边缘提取效果。

1 本文综合算法的提出与图像增强

1.1 本文综合算法的提出

经典的边缘检测算法是对原始图像中像素的某小邻域来构造边缘检测算子，常用的边缘检测算子有Prewitt、Log、Roberts和Canny算子等。近些年，随着数学形态学理论不断完善与发展，数学形态学在图像边缘检测中也得到了广泛的应用[6]。Prewitt算子的特点是抑制噪声效果好，但对边缘的定位不准确；Log算子的特点是边缘定位较准确，但对噪声较敏感，对图像中的某些边缘容易产生双重响应；Roberts算子的特点是计算时采用较少的像素，边缘定位准确，但是对噪声高度敏感。Canny算子是在图像处理中人们公认的功能较为强大的检测算子之一，但有时对于灰度分布不均匀的图像，容易将非边缘点检测为边缘。数学形态学是利用一个结构元素去探测一个图像，看是否能够将这个结构元素很好地填放在图像的内部，同时验证填放结构元素的方法是否有效。数学形态学的腐蚀算法会导致图像区域的分裂，而膨胀算法容易产生零星的像素点。

从目前的研究情况来看，单纯采用某种边缘检测算法很难实现脑外科CT图像准确的边缘提取。因而本文针对脑外科图像纹理复杂、细节丰富等特点，考虑到医学图像数据多层切片间的相关性，提出了一种综合的图像边缘检测算法，该算法集成了用平均值滤波器对图像增强，Canny边缘检测算子与数学形态学相结合的算法。

该算法的实现过程是在Matlab 7.5软件上对图像进行处理分析，运用了Matlab图像处理工具箱 （Image Processing Toolbox）中的大量函数。本文边缘提取算法的主要步骤为：

1）对原始图像运用平均值滤波器来对图像增强；

2）对增强后的图像用Canny算子进行边缘检测；

3）利用数学形态学中的膨胀算法进行边缘处理。

1.2 图像的增强

图像增强是数字图像处理过程中经常采用的一种方法，这种根据图像的特点或存在的问题采取的简单改善方法或者加强特征的措施称为图像增强（Image Enhancement）。图像增强的目标有2个：第一是改善图像的视觉效果，提高图像的清晰度；第二是使图像变得更利于计算机处理。所有的图像处理就是对这些组成图像的象素灰度值进行增或减的计算处理。从增强处理的作用域出发，图像增强的方法分为两大类：空间域方法和频域方法。由于CT图像存在大量的噪声，本文采用了平滑线性滤波器增强的方法，它是空间域的一种。平滑线性滤波器的输出是包含在滤波掩模邻域内像素的简单平均值，因此也称为均值滤波器[7]。

平均值滤波器定义如下，对于给定的图像 f（i，j）中的每个像素点（m，n），取其邻域S。设S含有M个像素，取其平均值作为处理后所得图像像素点（m，n）处的灰度值，即用一像素邻域内各像素灰度平均值来代替该像素原来的灰度值。邻域S的形状和大小根据图像特点确定，一般取的形状是正方形、矩形及十字形等，邻域S的形状和大小可以在全图处理过程中保持不变，也可根据图像的局部统计特性而变化，点（m，n）一般位于邻域 S的中心。

文中根据脑外科图像的特点和大量的实验比较，得出比较理想的效果是采用邻域S为正方形5×5邻域，像素点（m，n）位于邻域S的中心，共25个像素点，通过公式（1）计算该点的灰度平均值：

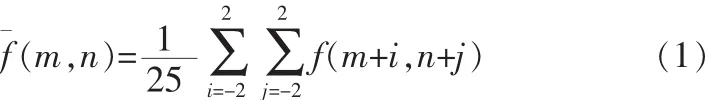
式中，f¯（m，n）为像素灰度平均值；m，n分别为像素点的横、纵坐标值；i，j分别为邻域S的横、纵坐标值。

原始图像如图1所示。在Matlab命令窗口中，首先应用imread（filename）函数将原始图像导入到Matlab中，然后应用filter2（fspecial（‘average’，5），I）/255 语句对原始图像进行增强，增强后图像如图2所示。

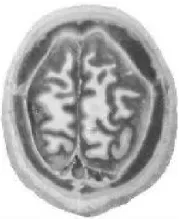
图1 原始图像Fig.1 Original image

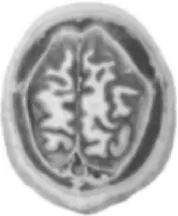
图2 图像增强后Fig.2 Image enhancement

从图2可以看出，经过平滑线性滤波器后的图像，去除了CT图像中因扫描存在的噪声、平滑了图像信号，为后面能够更好地进行边缘检测打下了基础。

2 Canny算子的边缘检测

边缘检测是对图像的边缘进行处理获得需要的边缘信息，常用的边缘检测算子有Prewitt、Log、Roberts和Canny算子等。每种边缘检测算子都有各自的优缺点，Prewitt算子抑制噪声效果好，但对边缘的定位不准确，Log和Roberts算子都是边缘定位较准确，但对噪声较敏感，因此本文选用了具有高信噪比、高定位精度和单边缘响应等优良性能的Canny算子。

Canny算子采用二维高斯函数的任意方向上的一阶方向导数为噪声滤波器，通过与图像卷积进行滤波，然后对滤波后的图像寻找图像梯度的局部最大值，以此来确定图像边缘[8]。由于噪声的影响，一个阈值的判断往往是不够的，边缘信号的响应只有近一半是大于这个阈值的，由此造成了边缘断裂。如果降低这个阈值，又会发现一些错误的“边缘”。为了解决这个问题，Canny提出了双阈值方法[9]。Canny算子进行边缘检测的具体步骤如下：

1）用二维高斯滤波器对图像进行滤波，图像通过二维高斯滤波函数。

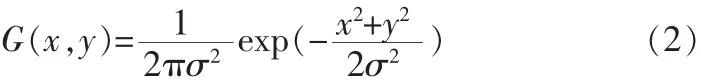
进行平滑，抑制图像噪声，其中σ为高斯滤波器参数，它控制着平滑程度。

2）用导数算子找到图像灰度沿着两个方向的偏导数（Gx，Gy），并计算出梯度的大小和方向。

3）对梯度幅值进行非极大值抑制。仅仅得到全局的梯度并不足以确定边缘，因此为确定边缘，必须保留局部梯度最大的点，抑制非极大值。若某个像素的灰度值与其梯度方向上前后两个像素的灰度值相比不是最大的，那么该像素值置为0，即不是边缘，这个过程称为“非极大值抑制”。

4）用双阈值法检测和连接边缘。对梯度取两次阈值Tl和T2，T1=T2，0＜α＜1，可根据噪声的大小适当调整。 用 T1、T2两个阈值对非极大值抑制图像进行双阈值化后，可得两个检测结果，分别记为图像1和图像2。图像l阈值较低，则保留了较多信息；图像2阈值较高，所以噪声较少，但会造成边缘信息的损失。于是以图像2为基础，以图像l为补充，连接图像的边缘。

应用 Matlab 图像处理工具箱中 edge（I，’ ’，thresh）函数，几种经典的边缘检测算子对增强后的图像进行边缘检测，效果如图3所示。

通过对图3的对比分析，可以清楚地看到：图 3（a）Prewitt算子对噪声有抑制作用，检测的图像没有较多孤立的边缘像素点，但对边缘的定位不是很准确，图像的边界损失较多；图3（b）Log算子检测的图像边缘信息损失较少，但对图像中的某些边缘产生双重响应；图3（c）Roberts算子对边缘定位比较准确，但存在较多孤立的像素点，抑制噪声能力差；图3（d）用Canny算子检测后的效果最好，由于Canny算子具有非极大值抑制和双阈值法连接边缘等优点，比前3种提取的边缘清晰而且连续，虚假边缘少，但是提取出的边缘仍然存在不光滑和断裂的现象。为了实现更好的边缘检测效果，下一步就要用本文提出的数学形态学算法来具体解决该问题。

3 数学形态学边缘检测

3.1 数学形态学的基本原理

数学形态学是一门综合了多学科知识的交叉科学，它建立在严格的数学理论基础上。其基本思想是用具有一定形态的结构元素 SE（structuring element）来度量和提取图像中的对应形状，以达到对图像的分析和识别的目的[10]。

膨胀和腐蚀是形态学的两个基本操作，膨胀过程是在图像中对图象的边界添加像素点，向外扩张，而腐蚀是它的逆过程。膨胀和腐蚀这两种变换都对灰度值变化明显的图像边缘较为敏感，膨胀可以填充图像中的小孔及图像边缘上较小的凹陷部分，腐蚀可以消除图像中细小的成分。下面介绍2个基本运算的定义：

膨胀运算定义为：

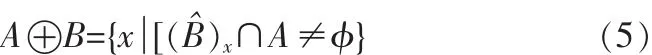
设A是原始图像，B是结构元素，式中A、B为Z2中的集合，φ为空集，Bˆ为B的映射，A被B膨胀，记为A⊕B，⊕为膨胀算子。该式表明膨胀过程为B首先做关于原点的映射，然后平移x。A被B膨胀是被所有x平移后与A至少有一个非零的公共元素。

腐蚀运算定义为：

图3 边缘检测Fig.3 Edge detection

设A是原始图像，B是结构元素，式中A、B为Z2中的集合，A被B腐蚀，记为AΘB。该式表明A被B腐蚀的结果是所有使B被x平移后包含于A的点x的集合。

3.2 数学形态学方法在图像处理中的运用

应用 Matlab图像处理工具箱中 imdilate（I，SE）函数，对经过Canny算子边缘检测后的图像进行数学形态法中的膨胀运算。利用数学形态学进行图像处理时，选择简单、表现力强的结构元素是关键，是形态变换中最重要的参数；其次，还要综合考虑目标体的清晰度和噪声的大小来选取结构元素的大小。一般目标体轮廓不清晰时，选择较小的结构元素；噪声颗粒较大时，选择较大的结构元素。本文根据脑外科图像的特点和大量的实验比较，采用平面结构元素为5×5的正方形，处理后的效果如图4所示。

图4 膨胀后效果图Fig.4 Dilated image

从图4中可以看到，经过膨胀后得到的边缘清晰而且光滑连续，基本上消除了图3（d）中所存在的边缘模糊和断裂现象，取得了较好的效果。

4 结 论

从以上的实验结果和分析可以看出：针对脑外科CT图像的纹理复杂、细节丰富等特点，本文提出的用平均值滤波器对图像增强、Canny边缘检测算子与数学形态学相结合的综合边缘提取算法，不仅具有简单快捷的处理能力，而且具有很好的边缘提取、较强的抗噪性能，提取出的边缘清晰连续，能够比较准确的提取脑外科CT图像的边缘，有效地保留了图像中的重要信息，为脑外科CT图像三维重建和虚拟手术的研究等打下了坚实的基础。

[1]M_engen S B， Marjunath B S， KenneyC.Image segmentation using multi-region stability and edge strength[C]//IEEE International Conference on Image Processing.Barcelona：Spain，2003：429-432.

[2]黄金国，戴志明，周培源.一种改进的基于梯度的图像边缘检测算法[J].武汉科技学院学报，2010，23（3）：33-35.

HUANG Jin-guo， DAI Zhi-ming， ZHOU Pei-yuan.An image edge detection algorithm based on gradient[J].Journal of Wuhan University of Science and Engineering，2010，23（3）：33-35.

[3]苏恒阳，袁先珍.一种改进的Canny的图像边缘检测算法[J].计算机仿真，2010，27（10）：242-245.

SU Heng-yang， YUAN Xian-zhen.An improved image edge detectionalgorithm ofCannyoperator[J].Computersimulation，2010，27（10）：242-245.

[4]Julez B.A method of coding TV signals based on edge detection[J].BellSystem Tech，1959，38（4）:1001-1020.

[5]Roberts L D.Machine perception of three-dimension solids in optica and electro-optimal information processing[C]//Massachusetts Institute of Technology Press,1966:157-197.

[6]Huang C P，Wang R Z.An intergrated edge detection method using mathematical morphology[J].Pattern Recgnition and Image Analysis，2006，16（3）：406-412.

[7]孙兆林.MATLAB 6.x图像处理[M].北京：清华大学出版社，2002.

[8]张斌,贺赛先.基于Canny算子的边缘提取改善方法[J].红外技术，2006，28（3）：165-169.

ZHANG Bin,HE Sai-xian.An improved method of edge detection based on Canny operator[J].Journal of Infrared technology，2006，28（3）：165-169.

[9]王家文，曹宇.MATLAB 6.5图形图像处理[M].北京：国防工业出版社，2004.

[10]张小琴,杨阔,郝葆青.基于Canny算子与数学形态学的细胞边缘提取[J].生物医学研究，2009，28（4）：275-279.

ZHANG Xiao-qin,YANG Kuo,HAO Bao-qing.Cell edge detection based on Canny operatorand Mathematical morphology[J].Journal of Biomedical Research，2009，28（4）：275-279.