基于蒙特卡罗计算方法的辐射剂量分布研究进展
2011-10-09刘卓
刘卓
北京大学人民医院 放射科, 北京100044
基于蒙特卡罗计算方法的辐射剂量分布研究进展
刘卓
北京大学人民医院 放射科, 北京100044
本文首先介绍蒙特卡罗方法的基本原理,及其在核物理实验,特别是辐射剂量计算等方面的应用;其次,介绍辐射计量学的基本知识和发展情况;最后,结合放射物理方面的知识,利用基于蒙特卡罗方法的EGSWIN软件,建立数学模型,并模拟计算电子束、光子束、正电子束在设定几何条件下的照射过程。
蒙特卡罗方法;辐射剂量计算;EGSWIN软件
蒙特卡罗方法是一种模拟随机过程的方法,在许多科学领域里都有着十分广泛的应用。在核物理技术上的重要应用是在放射治疗中辐射剂量的计算[1]。对放射治疗仪器,如加速器等进行剂量检验时通常使用三维水箱作为人体模型,因此,三维水箱剂量的模拟计算结果,在放射治疗的计划设计中具有参考价值[2]。放射治疗物理师以理论计算的结果为参考,进行实际的测量或者选择合适的放射源。本文以蒙特卡罗方法为理论基础,对三维水箱辐射剂量进行模拟计算。
1 理论基础
1.1 蒙特卡罗(Monte Carlo,MC)方法简介
蒙特卡罗方法又称随机抽样技巧,在实验物理中的应用是该方法的重要应用领域之一。蒙特卡罗方法具有逼真地描述真实物理过程的特点。在一定意义上讲,它可以部分代替物理实验,因此成为解决核物理实验中实际问题的非常有效的工具[3]。
半个多世纪以来,由于科学技术和电子计算机技术的发展,这种方法作为一种独立的方法,首先在核武器的研制与试验中得到了应用。蒙特卡罗方法虽然是一种计算方法,但与一般数值计算方法有很大区别。它是以概率统计理论为基础的一种方法。由于蒙特卡罗方法能够比较逼真地描述事物的特点和物理实验过程,解决一些数值方法难以解决的问题,因此该方法的应用领域日趋广泛。
1.1.1 蒙特卡罗方法的基本思想
为了说明蒙特卡罗方法的基本思想,先看一个例子:
例:射击问题(打靶游戏)[4]。设r表示射击运动员的弹着点到靶心的距离,g(r)表示击中r处相应的得分数(环数),f(r)表示弹着点的分布密度函数,它反映运动员的射击水平。该运动员的射击成绩为:
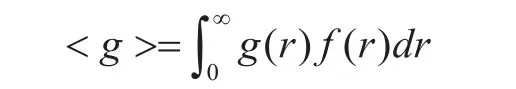
用概率语言来说,
现假设运动员进行了N次射击,每次射击的弹着点依次为 r1,r2,r3,…,rN,则N次得分g(r1),g(r2),g(r3),…,g(rN)的算术平均值为:

该值代表了该运动员的成绩。在该例中,用N次试验所得成绩的算术平均值作为数学期望〈g〉的估计值或积分近似值。
为了得到具有一定精确度的近似解,所需试验次数是极大的。通过人工方法做大量试验相当困难,甚至是不可能的。因此,尽管蒙特卡罗方法的基本思想早已被提出,却很少被使用。20世纪40年代以来,由于电子计算机的使用,使得人们可以通过计算机来模拟随机试验过程。也就是将试验过程,如将射击化为数学问题,在计算机上实现试验过程。假设射击运动员弹着点的分布为(见表1):

表1 射击运动员弹着点分布
用计算机做随机试验(射击)的方法是:选取一个随机数x,做如下判断:0 ≤x≤0.1为命中7环,0.1<x≤0.2为命中8环,0.2<x≤0.5为命中9环,0.5<x≤ 1为命中10环。这样就进行了一次随机试验(射击),得到了一次g(r),做N次试验后用公式(1)计算就可得到该运动员射击成绩的近似值。
由这个例子看出,蒙特卡罗方法常以一个“概率模型”为基础,按照它所描述的过程,使用已知分布抽样的方法,得到部分试验结果的观察值,求得问题的近似解。
1.1.2 蒙特卡罗方法的特点
(1)蒙特卡罗方法能够比较逼真地描述具有随机性质的事物的特点及物理试验过程。
(2)蒙特卡罗方法可以部分取代物理试验,甚至可以得到物理试验难以得到的结果。
(3)用蒙特卡罗方法解决实际问题,可以直接从实际问题本身出发,而不从方程或数学表达式出发,有直观、形象的特点。
1.2 蒙特卡罗方法的应用范围
蒙特卡罗方法主要应用范围包括:粒子输运问题、统计物理、真空技术、激光技术等。
1.2.1 在辐射剂量学中的应用
20世纪80年代中后期,随着计算机技术的发展和运算速度的提高,蒙特卡罗方法在粒子输运方面得到了广泛的应用。它的主要思想是:当所求问题的解是某个事件的概率,或者是某个随机变量的数学期望,或者是与概率、数学期望有关的量时,通过某种数值试验的方法,得出该事件发生的频率,或者该随机变量若干个具体观察值的算术平均值,通过它得到问题的解。许多关于辐射剂量学、放射治疗物理和辐射防护的问题都可以利用蒙特卡罗技术来解决。蒙特卡罗技术在这些领域中的应用在近20年里有了极其显著的提高,其主要原因在于数据处理速度的迅速提高和费用的降低,以及大型通用蒙特卡罗程序包的发展。
粒子输运问题具有明显的随机过程性质,粒子在介质中的运动规律是大量粒子所表现出来的一种统计规律。在计算机上用MC方法模拟粒子输运过程,实际上就是模拟一批(10~100万个)粒子在介质中运动的状况,即一个一个地跟踪这批粒子在介质中的随机游动过程,并在跟踪过程中记录一些有用的信息,从而得出粒子的近似运动规律。
蒙特卡罗技术在辐射剂量学中的应用[5]:
(1)光子或电子探测器的响应函数的计算。光子或电子探测器(如碘化钠、硅、高纯锗等)响应函数的蒙特卡罗模拟是蒙特卡罗方法应用的一个典型方面。由于光子与探测器内物质发生反应后,产生次级光子和电子,而电子和正电子在输运过程中又会产生光子。这种光子与电子的耦合输运过程是非常复杂的,用一般数值方法难以解决。蒙特卡罗方法能够在较少近似的情况下,真实地模拟这种复杂的物理过程,因而成为计算此类问题的有效工具。
(2)吸收剂量及其相关参数的计算。粒子在介质中任意点处的吸收剂量的计算是蒙特卡罗技术在辐射剂量学中应用最广泛的一个方面。尤其是对粒子在几何形状复杂的非均匀介质中的能量沉积的计算,蒙特卡罗方法更是具有独特的优势,虽然其计算速度目前仍不能达到某些应用的要求,但对于速度不太高的场合,蒙特卡罗模拟的精确性和可靠性都是非常高的。
(3)蒙特卡罗技术在空腔电离室理论研究方面的应用。在研究各种空腔电离室理论及应用中,蒙特卡罗计算的最大贡献在于通过这种计算去获得许多无法从实验中得到的物理量和修正因子,在计算中某些物理过程可被人为设置开或关,从而使我们发现是什么过程引起了某种特别的现象。
以上三个方面是蒙特卡罗技术在辐射剂量学中的最有代表性的应用,实际上,在许多的分支领域,利用蒙特卡罗技术都是一个十分有效的研究工具,如固体电离室的吸收剂量——光子注量转换因子的计算,轫致辐射谱的计算等。而理论计算和实验工作的相辅相成,必将推动辐射剂量学研究的不断深入和发展。
1.2.2 在肿瘤放射物理学方面的应用
由于蒙特卡罗方法是基于计算机模拟物理的思想,能够抓住物理过程的数量和几何特征,利用数值方法加以仿真,比较逼真地描述事物的特点及物理过程。因此,该方法是求解辐射输运问题和粒子能量沉积的一种相当成熟、实用和有效的方法,在肿瘤放射物理学尤其是远距离放射治疗中的应用已越来越广泛[6]。
粒子与物质相互作用时服从统计学规律,发生作用的位置、作用的形式(如对光子而言,有光电效应、康普顿效应、电子对效应),发生作用后粒子可能被吸收或散射,散射粒子的运动方向和能量、两次作用位置间的距离等参数均是随机变量。蒙特卡罗方法可以模拟粒子与物质相互作用的全过程,通过模拟10万甚至100万个粒子的输运过程,就可以比较精确地计算出粒子束与物质相互作用的宏观特征,如注量分布、吸收剂量分布。蒙特卡罗方法的优点是可以处理粒子输运的各种复杂情况,尤其是一些难以进行实验测量的情况。
蒙特卡罗方法在肿瘤放射物理学中的应用:
(1)外照射源模拟。以加速器产生的X射线的输运过程为例,蒙特卡罗技术是用随机抽样技术去模拟以下两个过程:① 由加速器X射线靶产生的X射线和一级准直器、均整器产生的散射X射线组成的初始射线和散射线的能谱及离轴分布;② 初始射线及散射线光子在介质中的输运过程。
目前已有蒙特卡罗程序,如EGS4和 EGS-BEAM等[7],不仅能模拟均匀介质中上述两种过程,而且能够精确模拟不均匀介质中,光子和经一级和二级碰撞产生的次级电子的径迹,计算它们的能量沉积。对一个治疗射野,蒙特卡罗模拟跟踪上亿个光子事件的能量沉积过程。
(2)外照射时模体内辐射场模拟。模拟粒子束进入模体能量沉积的过程,包括粒子通过加速器与模体表面之间的空气间隙的作用过程。除了可以准确给出模体内离轴比和百分深度剂量,以及射野的大小外,还可以求解除剂量以外的一些物理量,比如能谱和初始射线、散射线的平均能量。
(3)剂量仪响应模拟。电离室的能量响应和室壁修正因子以及胶片测量中胶片灵敏度随能量变化曲线问题都可以用蒙特卡罗方法解决。胶片剂量仪具有很多优点,可以测量一个平面内所有点剂量,具有高的分辨率,而且可以测量不均匀固体介质中的剂量分布,但由于其灵敏度随粒子的能量变化造成光学密度校正曲线有偏差,影响测量结果。蒙特卡罗方法可修正胶片随深度和射野大小变化的灵敏度曲线,以及为测量结果如半高宽和半影作理论验证。
(4)外照射治疗计划应用。由于蒙特卡罗方法运算速度慢,还不能直接用于治疗计划的制定,而是对计划中所采用的计算规则和技术作理论验证,以及为新的治疗计划提供配置数据。放射治疗的基本目标是努力提高放射治疗的治疗增益比,即最大限度地将放射线的剂量集中到病变(靶区)内,杀灭肿瘤细胞,而减少对周围正常组织和器官的损伤。因此理想的放射治疗技术应按照肿瘤形状给靶区很高的致死剂量,而靶区周围的正常组织不受到照射。适形调强放射治疗是一种提高治疗增益比的较为有效的物理措施,但由于缺乏治疗验证措施和计划评估手段,限制了适形调强放射治疗的广泛应用。建立在CT影像基础上的蒙特卡罗三维计算,可给出各种适形野以及由多野结合、楔形板、组织补偿技术等造成的不规则野的剂量分布,并提供理论验证或各种配置数据。
(5)腔内放疗源周围辐射场模拟。主要应用在近距离放射治疗中,如研究125I在人体内的剂量分布,利用蒙特卡罗方法计算放射性液体球囊在血管组织内的剂量分布等[8]。
随着计算机技术的迅猛发展,蒙特卡罗方法在肿瘤放射物理学中的应用将会越加广泛。当然,蒙特卡罗方法在解决粒子输运问题中依然存在概率性质的误差等问题。除此之外,经验证明,只有当系统的大小与粒子的平均自由程可以相比较时,即系统大小为10多个平均自由程时,结果较为满意。而对于大系统,算出结果偏低,但是数值方法适应于大系统的计算,得到结果较好。现在已经有人将两者结合起来使用,取得了一定效果。
1.3 蒙特卡罗方法应用软件
目前已有蒙特卡罗程序,如EGS、MCNP 等,不仅能模拟均匀介质中上述三种过程,而且能精确模拟不均匀介质中,光子和经一级和二级碰撞产生的次级电子的行迹,并计算它们的能量沉积。
1.3.1 MCNP 程序
MCNP程序全名为Monte Carlo Neutron and Photo Transport Code。由美国洛斯阿拉莫斯(LANL)国家实验室研制,是当前最高水平的通用的科学计算程序。用于处理连续能量、时间相关、三维几何的中子-光子-电子辐射输运问题。MCNP从1977年6月产生第1个版本后,不断更新,到1997年3月产生了最新版本MCNP-4B,可以在各类计算机上运行。
1.3.2 EGS 程序
EGS程序的全称为 Electron-Gamma Shower,模拟在任意几何中能量从几个keV-几个TeV的电子-光子蔟射过程的通用程序包,由美国 Stanford Linear Accelerator Center提供,1979年公开发表。EGS4是1986年发表的第4个版本,EGS4计算程序在国际上有着广泛的应用。在辐射物理方面,主要计算加速器产生的辐射剂量分布,设计屏蔽系统,研制剂量测量仪等。在医学物理方面,模拟计算射线在人体中产生的剂量分布及衰减,进而确定治疗方案等。在西欧和北美的一些国家,已被广泛应用于医院,用于放射治疗及诊断中的剂量计算。自从1979年公布以来,已有近千篇相关论文发表,其可靠性得到了国际社会的认可。
1.3.3 EGSWIN 程序
针对EGS4在用户接口方面存在的缺陷,利用VC++开发了基于Windows平台的EGSWIN计算程序包,实现了图形化输入、几何区域处理、并行计算、多记录方式输出、几何实体与粒子径迹显示等,极大地克服了原有EGS4使用上的局限,体现了当前国际上EGS的开发方向,并在一定程度上推动了EGS系列的发展。通过使用本程序,用户可以仅进行简单而直观的输入几何实体的工作,就可以实现区域的定义,极大地提高了EGS的使用效率。
1.4 辐射剂量计算方法的最新成果
快速精确耦合剂量计算方法,可以克服快速简单剂量计算方法和精确MC剂量计算方法各自的缺点。考虑人体不同解剖结构和组织不均匀程度来实现剂量计算方法的耦合,即对组织结构简单、均匀性较好的部位,采用一维或二维的快速剂量计算方法,而组织不均匀部位或一些特殊部位(不同组织分解面、由医生圈划的肿瘤区和重要器官区域)则使用精确的三维剂量计算方法。在同一个病例的计算中,这些不同剂量计算方法的选择与耦合,可以满足各种人体几何、组织的精度要求,合理的边界条件选取和处理是关键。
2 模拟计算
2.1 计算模型与方法
模拟测量装置:三维水箱,结构如图1所示。

图1 模拟测量装置结构图
现简要说明,选择水箱作为人体模型,进行剂量测量的原因:临床剂量测量不可能在真人体内直接进行,必须寻找最接近人体组织的等效材料作为替身。由于放射治疗所用的X(γ)射线的能量远远高于放射诊断的常用能量,在此能域内主要是康普顿效应和电子对效应的作用,所以体模材料只要有与人体相近的有效原子序数、相近的每克电子数、相近的质量密度和足够大的散射体积,就可以获得相近的测量结果。目前,世界各地自动扫描测量应用最广泛的体模是三维水箱[9];临床治疗模拟测量最常用的是人体仿真剂量体模。其他组织等效材料如石蜡、聚乙烯等也较常用。人体90%以上是有碳,氢,氧,氮组成的有机化合物。实测表明,人体肌肉和其他软组织对治疗射线的吸收与散射几乎与水相同,心、肝、脾、肾、肠、胃等组织器官的散射与吸收也与水很相近。而世界各地的水都一样,廉价易得,性能稳定,便于扫描测量,所以各种水箱是放射治疗剂量学测量的理想模体。
具体的实际测量方法是,选择射线源至水面100cm,照射面积以10cm为半径的圆形照射野,开机出束后使电离室探测器在射线中心轴上由水表面向水深层进行扫描测量,同时用X-Y记录仪作出剂量深度曲线。
三维水箱在放射治疗中具有重要的应用价值,而利用计算机模拟三维水箱的能量沉积对实际的测量工作具有重要的指导和预测作用。因此,选择三维水箱的相关模拟计算作为本次设计的内容,并且利用EGSWIN软件作为模拟计算的工具。
在使用EGSWIN程序进行模拟计算时,利用软件的图形输入程序,直观、方便地建立虚拟三维水箱模型:纵向紧密排列10个圆柱体,每个圆柱体厚2cm,半径10cm,并设定每个圆柱体以水做介质。以此10个圆柱体模拟一个深20cm,半径10cm的水箱。
图2为EGSWIN 图形输入程序,在此界面内,排列10个圆柱体。

图 2 EGSWIN 图形输入程序界面图
2.2 计算结果与分析
(1)分别计算能量为6MeV的电子、正电子、光子放射源,照射水箱,在水箱中不同深度层中能量的沉积(如图3~5所示):

图 3 6MeV电子照射的结果
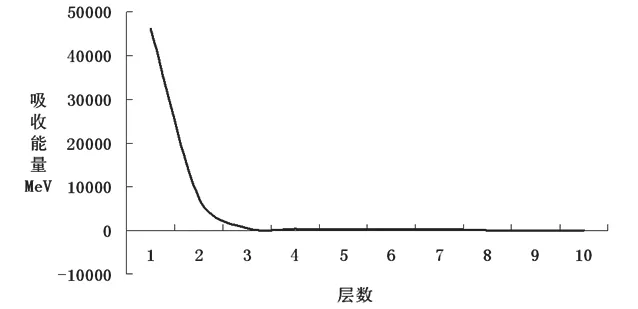
图 4 6MeV电子照射的结果
观察以上数据及三幅图,可以直接得到如下结果:首先,正电子与电子照射的能量分布相似,其明显特点是,吸收能量主要分布在第一、第二层介质,即距离水模表面4cm内。
其次,光子照射的能量分布与正电子与电子照射的能量分布有明显区别,吸收能量在10个水介质层,即20cm内分布比较均匀,表面第一层的吸收能量相对较少。

图 5 6MeV电子照射的结果
以上结果符合相关参考资料中的数据[4]以及放射物理相关理论。光子是不带电粒子,且无静止质量,与物质间的相互作用属于非直接电离,有明显的剂量建成效应,其穿透能力比电子、正电子大,射程比电子、正电子长,能量可以传递给较深的水介质。电子、正电子与物质间的相互作用属于直接电离,因此射程短,无明显的剂量建成效应,能量大部分传递给表浅的水介质。
(2)1MeV和 5MeV光子源分别照射水箱的对比:
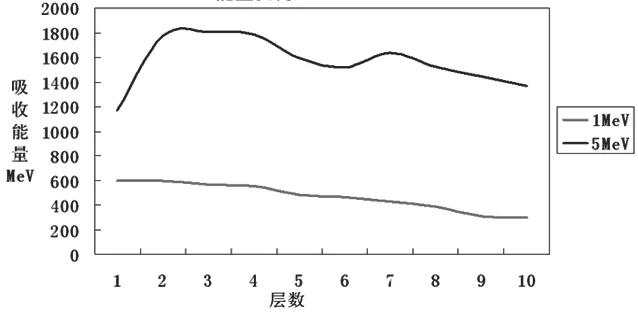
图 6 能量沉淀
从图6中可以看出,5MeV光子源在水箱中的能量沉积明显高于1MeV光子源,而且在随深度增加,变化的趋势也有明显不同。在放射治疗过程中,通常根据这种深度剂量曲线选择合适的放射源能量,给予特定深度的病变组织合适的剂量,达到预期的效果。

图 7 1MeV光子频谱
从图7~8中看出,每层介质对某一特定能量或频率的光子吸收明显高于其他能量或频率,利用这个结果,选择特定放射源,在给定介质中大量沉积某频率的光子。由于生物效应与光子频率有一定关系,因此,通过选择光子频率,可在一定程度上控制生物效应,从而达到预期的治疗效果。
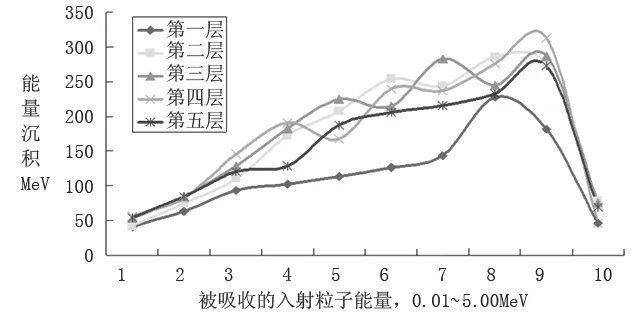
图 8 5MeV光子频谱
3 结束语
本研究对三维水箱中的剂量分布进行了模拟计算,即对三维水箱进行不同能量,不同种类的放射源照射结果的对比、计算不同深度介质中能量沉积的频谱。这些结果符合放射物理学的相关理论,并且对三维水箱的实际测量工作具有参考价值。以上结果可以证明,蒙特卡罗模拟方法可以相当准确地模拟计算辐射剂量的分布,对核物理实验,尤其是放射治疗方面具有重要的使用价值。
从计算结果可以看出,EGSWIN软件无法以表格或图表格式输出计算结果,尤其是大量的结果数据,不便于后期处理和运算。但是,利用EGSWIN软件进行粒子输运的计算,其准确性是能够得到保证的,因为EGSWIN本身就基于清晰易懂的物理过程,具有灵活性;是一个经过各种基准实验验证了的程序;它的开放的结构,基于很多用户的贡献,其本身就是开放软件。目前已被广泛应用于医学物理,自从第一次公布以来,已有近千篇有关论文发表。
[1]许淑艳.蒙特卡罗方法在实验核物理中的应用[M].北京:原子能出版社,1996.
[2]胡逸民,等.肿瘤放射物理学[M].北京:原子能出版社,1999.
[3]刘宗良,李强,赵平华,等.蒙特卡罗模拟方法及其在辐射计量计算上的应用[J].湖南人文科技学院学报,2006,(6):24-27.
[4]P A Lovey,D G LewisI A M Al-Affan, C W Smith. Comparison of EGS4 and MCNP Monte Carlo codes when calculating radiotherapy depth doses.Phys[J].Med.Biol.1998,(43):1351-1357.
[5]郭勇.辐射剂量学概论[J].中国辐射卫生,2005,14(2):86-90.
[6]俞受程,等.现代肿瘤放射治疗学[M].北京:人民军医出版社,2000.
[7]冉蜀阳,傅玉川,罗正明.利用蒙特卡罗程序EGSnrc实现电子束辐照剂量分布的计算和电子束辐射加工工艺的优化[J].辐射研究与辐射工艺学学报,2002,(2):34-38.
[8]孙雨云.蒙特卡罗方法在肿瘤放射物理学中的应用[J].实用医技杂志,2007,(17):87-88.
[9]王春燕,刘漪,曲典,等.三维水箱模体中辐射剂量分布的模拟研究[J].核电子学与探测技术,2009,(2):80-82.
Research on Radiation Doses Distribution Based on Monte Carlo Method
LIU Zhuo
Radiology Department, People's Hospital,Peking University, Beijing 100044,China
O242.2;R730.5
B
10.3969/j.issn.1674-1633.2011.02.018
1674-1633(2011)02-0062-05
2010-09-05
作者邮箱:l_zhuo@hotmail.com
Abstract:This article first introduces the basic theory of Monte Carlo method,and its use in nuclear physics experiments,especially in radiation doses calculation. Secondly,it introduces the basic knowledge and development of radiation metrology. And finally, it proves that EGSWIN is able to calculate the radiation doses in certain experiments,available to three kinds of sources including electron,photon and positive electron,with great simplicity and directness.
Key words:Monte Carlo method; radiation doses calculation; EGSWIN
