高分辨雷达目标检测方法研究

刘 冰 罗丁利

(西安电子工程研究所 西安 710100)

1 引言

雷达恒虚警(CFAR)检测已逐渐成为现代雷达的一项标准技术。恒虚警处理的基本原理就是根据检测单元附近的参考单元估计背景杂波的能量并依次调整门限，从而使雷达信号检测满足纽曼－皮尔逊准则的处理方法，雷达所处的杂波环境很复杂，对其的估计方法很多，所以恒虚警的处理方法也很多。依据杂波类型是否可知可将恒虚警检测方法分为参量型和非参量型。参量型常用的CFAR处理方法有均值(ML)［1］类的 CFAR 和有序统计量(OS)［1］类的CFAR。参量型恒虚警监测器均基于瑞利型杂波背景提出的。对于高分辨雷达，其杂波回波幅度服从非瑞利分布，如对数分布，韦布尔分布和K分布，因此雷达目标检测器需要重新设定门限。

本文首先分析了高分辨雷达的杂波回波特性，给出了回波模型，在此基础上研究了非瑞利杂波背景下的高距离分辨雷达的检测方法。

2 高距离分辨雷达杂波回波模型的建立

2.1 高分辨雷达杂波统计特性

雷达杂波是来自雷达分辨单元内的许多散射体的回波矢量和。在中低分辨力条件下，当回波单元足够大使得其包含大量散射体且其回波强度分布满足中心极限定理时，合成回波是高斯的，从而雷达包络检波器的输出是瑞利分布;在现代高分辨力雷达或机载雷达条件下，因为小的距离分辨单元使得杂波幅度概率密度函数有较高的尾部，或者，小的散射体在大部分时间内被大的起支配作用的散射体所遮挡，分布常常偏离瑞利特性，常用对数正态分布、韦布尔分布(适用于近距离严重杂波环境)和K分布(适用于海杂波)来描述。

实际工作的雷达，如脉冲体制雷达，是在多个脉冲观测基础上进行检测的，这样积累的杂波样本值之间是相关的，因此，在杂波模拟中，需要同时考虑杂波的幅度分布和其相关性。

2.1.1 高分辨雷达杂波幅度模型

当雷达分辨率较高且擦地角很低时，杂波的幅度分布可用对数正态分布，韦布尔分布和K分布来描述，在这里我们以对数正态分布为例。

对数正态分布适用于低入射角复杂地形的杂波数据或者平坦区高分辨率的海杂波数据。对数正态分布的概率密度函数为:

式中σ为正态分布的标准差，u为对数正态分布的均值。随着σ的增大，其中概率密度分布的拖尾变长。

2.1.2 高分辨雷达的杂波功率谱模型

由于风速，雷达平台运动以及扫描天线转动的影响，同一分辨单元不同脉冲回波之间具有相关性，定义为杂波信号的时间相关性，描述时间相关函数的频谱一般为高斯谱:

式中，fc杂波中心频率;σc是杂波均方谱宽。

2.2 线性调频脉冲压缩雷达杂波回波模型

带宽B，时宽为T的线性调频矩形脉冲信号的包络表达式:

其中A为信号幅度。根据雷达分辨理论，雷达距离分辨率等于c/2B，因此雷达波束照射区覆盖N=TB个距离分辨单元。当线性调频信号的发射照射地面时，地面上各反射点的回波都要持续脉冲宽度T的时间。在高分辨率条件下，杂波的回波可以看作是N个相邻的点目标的回波在时间和空间上的叠加，相邻两个距离分辨单元的回波延迟。总的杂波回波信号为N个分辨单元杂波回波的错位叠加，在一个脉冲重复周期内，叠加后杂波回波包络表达式为:

其中Ki为与雷达方程有关的幅度系数［5］;ki为目标散射强度，高分辨率情况下ki服从非瑞利分布。由于杂波的回波和雷达的发射信号是相干的，所以匹配滤波器不仅对目标的回波实现脉压同时对杂波的回波实现脉压。理论分析表明，在时域上两个相邻距离单元的回波通过匹配滤波器是完全分开的。因此第i个杂波回波单元通过匹配滤波器后的输出:

每个杂波单元匹配后输出为一个宽度为τ=1/B的窄脉冲，脉压比，脉冲幅度为输入信号幅度的倍［2］，k'i=ki·据此我们可以直接在匹配滤波器后构造杂波回波模型，该模型无需考虑各个距离单元的回波在空间上和时间上的叠加问题，直接利用各个距离单元杂波回波幅度的倍构成匹配杂波后的杂波幅度模型，在不改变杂波统计特性的条件下达到快速仿真的目的。

3 高距离分辨雷达目标检测方法

由上述分析可知，高距离分辨雷达下的目标回波可看作是多散射点目标回波的叠加，如果采用CA－CFAR检测，检测概率将随着目标占据单元数的增加而显著下降，因此，在高距离分辨雷达下常采用OS－CFAR检测。一种有效的高距离分辨雷达目标检测方法是，首先采用普通雷达的恒虚警方法对一维距离像进行检测，以获得强散射中心的数目和位置，然后利用目标内在的相关性进行二次门限检测。

第一门限的检测可根据具体情况选用普通雷达的恒虚警检测方法。对于高距离分辨雷达，一般选用基于有序统计量的恒虚警检测方法。第二门限的检测一般有两种方法，一种是M/N［5］检测。另一种是基于位置信息的距离段联合检测，又称IM/N［5］检测，该方法可以看作是M/N的逆过程。

本文以服从对数正态分布的杂波为背景研究高分辨雷达的目标检测方法。

3.1 第一门限检测

3.1.1 服从对数正态分布的杂波恒虚警概率

设随机变量Y服从对数正态分布，即:

与 δ2应满足 T= δ2。

3.1.2 杂波的参数估计及门限K的设置

对数正态分布的杂波恒虚警概率是把对数正态转化为正态分布来计算的，令x=lnη，则x服从N(lnμ，δ2)。因此，对数正态分布的两个参数为 μ =exp(mx)，δ2=v(x)。

给定的虚警概率对应着一定的检测门限T，在自适应门限检测中，为了达到恒虚警的目的，需要给定响应的检测门限系数k，k可由下式获得:

式中mη表示所得杂波数据的数学期望。

3.1.3 TM－CFAR［4］

OS-CFAR被证明是在多目标环境下较传统的CA-CFAR有较好的检测性能，高距离分辨雷达目标信号检测可以看作是在非瑞利杂波背景下对多目标的检测，因此一般的高距离分辨雷达都采用OSCFAR作为第一门限。OS-CFAR将参考单元由小到大进行排序，选取第K个值作为总的杂波功率水平估计，而由此派生出了另一种基于有效统计量的TM-CFAR，即对各参考单元由小到大排序后，消减掉较小的r1个值和较大的r2个值，取中间值做平均处理作为总的杂波功率水平估计。TM-CFAR检测器的结构如图1所示。

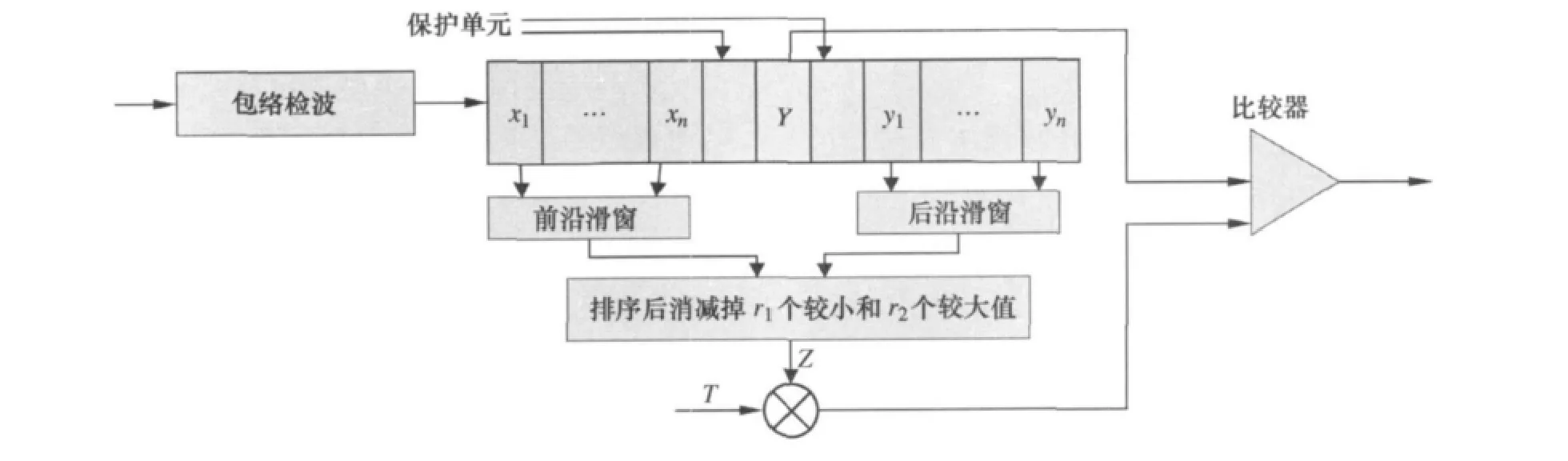
图1 TM-CFAR检测器原理方框图

3.2 第二门限检测

对于高分辨雷达，采用第一门限后，目标的回波可能占据多个距离单元，因此一个目标的回波在经过第一门限后会被认为多个目标，第二门限检测就是为了解决这个问题而提出的。第二门限检测最典型的方法是M/N检测，它以N个单元中至少有M个强散射点即判断有目标，否则判定无目标。其中N为设定的窗所占的距离单元数，依实际情况而定，而M是目标回波强散射点数目，一般的军事目标强散射点数为4～5个。M/N检测一般采用滑窗检测，每移动一次滑窗统计一次窗内的散射点数目，与给定的判决门限M相比较，高于该门限就认为有目标。

4 仿真验证

为了验证以上分析的有效性，我们在MATLAB上进行了仿真，这里首先采用ZMNL法产生服从对数正态分布的杂波，然后在此杂波上叠加两个离得比较近的目标，形成多目标环境，其中一个为强目标，原始目标回波如图2所示，其中b为放大的细节图。为了说明TM-CFAR相对于CA-CFAR的有效性，对于第一门限检测我们分别采用了这两种方法，检测结果如下所示，图3为CA-CFAR检测结果，其中a为CA-CFAR自适应检测门限，b为细节放大图;图4为TM-CFAR检测结果，其中a为TM-CFAR自适应检测门限，b为细节放大图。从图可看出CA-CFAR处理所形成的自适应门限由于高分辨下目标占据单元个数增多以及多目标的存在而有所提高，另外从细节图中可看出两个目标之间的相互影响，其中，大目标由于附近小目标的存在使得自适应门限抬高，检测性能下降，小目标由于受到大目标的影响自适应门限的抬高而无法被检测到;而在多目标环境下，由于目标相对于杂波的幅度较大，排序时大多位于后面位置，如参考单元窗内有r个单元被强目标占据时，如果r＜r2，目标的存在一般不会影响到Z值的估计，因而对其检测性能影响较小，目标之间也不会受到相互影响，两个目标都能被检测到。另外从图中可以看出在杂波边缘处CA-CFAR和TM-CFAR都存在一定的凹陷，使得检测性能在杂波边缘处下降，对于这种情况我们通常可以在杂波边缘处进行一些其它处理，例如在边缘处采用单边恒虚警，或者可采用GO-CFAR，由于本文重点关心目标处的检测性能，在这里就不详细研究，具体可参看文献［4］。图5为TM-CFAR的检测结果经过二次门限检测即M/N检测后的结果，可以看出第一门限检测后的一些过门限的杂波经过二次门限的相关处理完全去掉，只留下比较干净的目标，并且将两个目标完全区分开。

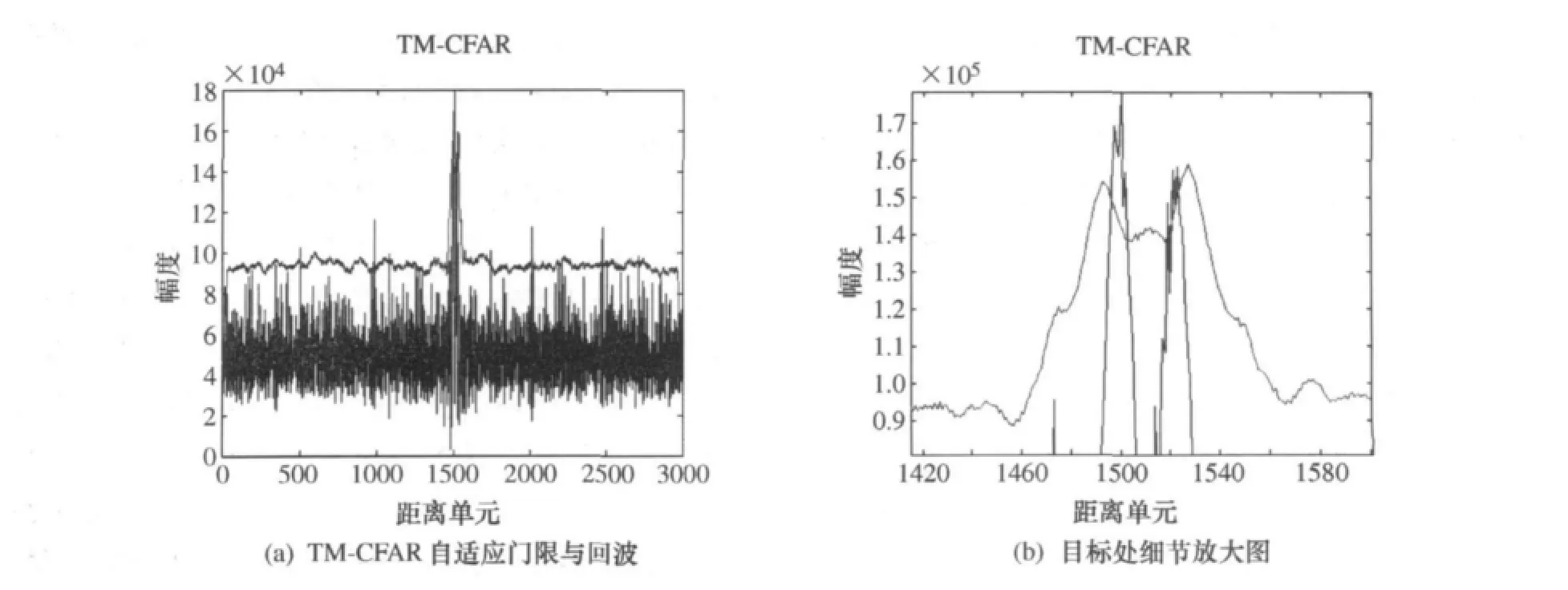
图4 TM-CFAR自适应门限与回波

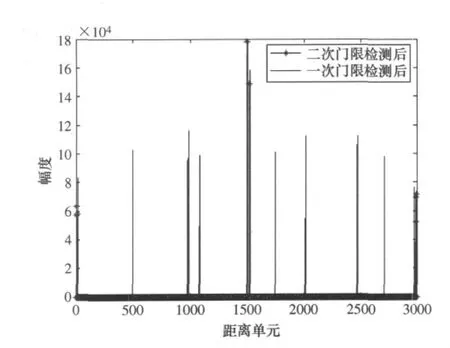
图5 TM-CFAR与M/N相结合的检测结果

5 结论

本文首先讨论了高距离分辨雷达的杂波回波模型，在此基础上研究了非瑞利杂波背景下适用于高分辨雷达的恒虚警检测，即采用TM-CFAR与M/N检测相结合的方法。这种检测方法以常规雷达恒虚警检测方法作为第一门限，再依据高距离分辨目标回波扩展后的位置信息设立第二门限，以达到良好的检测门限，最终通过仿真验证了该检测方法的有效性，具有重要的现实意义。

［1］何友，关键，彭应宁等.雷达自动检测与恒虚警处理［M］.北京:清华大学出版社，1999.

［2］西北电讯工程学院《雷达系统》编写组.雷达系统［M］.北京:国防工业出版社，1980，118－128.

［3］张慧燕，吴顺君.自适应门限下杂波恒虚警算法［M］.西安:西安电子科技大学出版社，2000.

［4］祝本玉，毕大平，王正.两种典型的CFAR检测器性能仿真［J］.舰船电子对抗，2008，31(2).

［5］马凡妮.高距离分辨雷达目标检测方法研究［M］.电子科技大学，2006.