雷达网对抗远距离支援干扰检测能力分析

刘 勇 李国君

(中国人民解放军92941部队 辽宁葫芦岛 125001)

1 引言

比较而言，雷达网较单部雷达具有更强的信号探测跟踪能力和更广阔的空域覆盖范围，且在雷达网的重叠区域内具有更高的信号检测能力和检测概率［1，2］。受到干扰时雷达网融合规则的选取尤为重要。文献［3］中研究了各部传感器观测相关条件下，融合中心最优融合规则问题，并讨论了融合系统检测性能与传感器判决之间相关系数的关系;文献［4］从空域的角度讨论了区域警戒雷达网的分布检测性能及雷达数目与总检测概率的关系，并对工程应用中的部署雷达数目进行了讨论，同时在其文献［5］中提出了利用Neyman-Pearson融合准则改善区域雷达网分布式检测性能的方法;文献［6］中针对雷达网数据融合提出了一种基于Neyman-Pearson融合准则的分布式并联融合系统检测理论的系统性能优化算法;文献［3，4，5，6］研究了雷达未受干扰条件下，不同融合规则时的检测性能。文中针对远距离支援干扰条件，分别利用秩K准则和Neyman-Pearson准则的分布式检测理论，仿真出干扰状态下雷达网的检测概率分布曲线图，克服了以往利用空间单个点检测概率描述雷达网性能的局限性，对雷达网在干扰下的检测概率进行了更精确、更直观的评定。

2 远距离支援干扰条件下雷达网检测概率模型分析

为了分析远距离支援干扰条件下雷达网检测概率，首先需要求解单部雷达受到远距离支援干扰后的检测概率，然后将解算出的单部雷达受到远距离支援干扰后的检测概率作为输入分量输入秩K准则或Neyman-Pearson准则进行分析，从而完成对雷达网检测概率的分析与评价。

2.1 远距离支援干扰条件下单部雷达的检测概率Pdi的求解模型

单部雷达受到远距离支援干扰后的检测概率由雷达接收机输入端的信干比决定，据此建立远距离支援干扰条件下雷达探测目标模型，其几何关系如图1所示［8］。为了便于研究，假设目标为雷达反射面积固定的典型目标。

图1 目标、雷达和干扰机之间的空间关系

雷达接收机输入端的信干比(目标回波信号功率和干扰信号功率加噪声功率之比)为:

其中，干扰机、目标与雷达的相对波束张角为θJ;雷达收到的目标回波信号功率Prs和PrJ分别为:

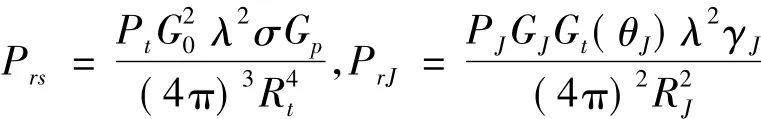
式中，Pt、G0分别为雷达发射功率和天线增益;σ为目标的雷达截面积;λ为波长;Rt为雷达与目标之间的距离;PJ为干扰发射功率;GJ为干扰发射天线增益;Gt(θJ)为雷达天线在干扰方向的增益;γJ为干扰信号与雷达信号的极化失配损失系数(通常干扰信号为圆极化，雷达天线为线极化，γJ=0.5);RJ为雷达与干扰机之间的距离。

本文使用了第一类目标起伏模型SwerlingⅠ，慢起伏，瑞利分布。截面积概率密度函数为p(σ)=，式中为目标起伏全过程的平均值。

因此，起伏模型SwerlingⅠ的概率求解公式为:

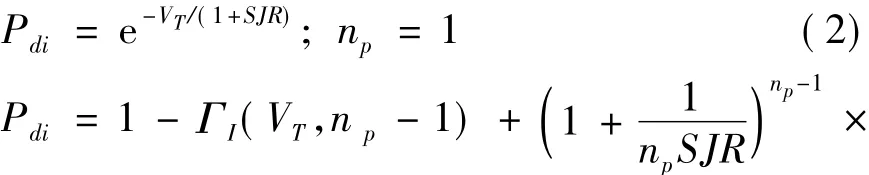
其中np为脉冲积累个数;Pfi为雷达虚警概率;nfa为虚警数。

2.2 秩K融合规则检测概率模型

在决策融合中，融合中心采用秩 K融合规则［7］。假定有n个局部检测器，其中至少有K(1≤K≤n)个检测器判定目标存在，则融合中心就确定目标存在，此即秩K融合规则。对应K=1，称为“OR规则”，对应K=n，称为“AND规则”。

在未加权的情况下，秩K融合规则用于n个局部检测器，分布式检测中心的检测总概率PD和虚警总概率PF可表示如下:

其中Pfj，Pdj为各雷达的虚警概率和检测概率且统计独立，i=1，2，…，n，是n个局部检测器中i个局部检测器检测概率全部可能乘积的和，同样适应于是i取p的组合。

在检测中心采用秩K规则优化时，对K的选择必须进行全面地衡量。仿真试验中应采取:分别计算秩K从K=1到n时相应的检测概率和虚警概率，最佳的秩K融合规则可以由仿真结果分析选择，这主要取决于各雷达的检测性能和雷达网的检测指标。

2.3 Neyman－Pearson融合规则检测概率模型

决策-概率融合模型是在融合检测中心采纳Neyman-Pearson准则进行数据融合，既保持融合检测的虚警概率，又使其检测概率最大［7］。这种最优化方式极具意义，它在提高系统检测性能的同时，又保证了整个系统具有恒虚警的特性［9］。

设雷达网部署雷达站数目为n，融合检测中心输入向量 D=(d1，d2，…，dn)(di为第 i个雷达站的判决输出，若判定目标存在则di=1，否则di=0)，可以有 N=2n种可能的实现，记为 Di，i=1，2，…，N，融合中心的恒虚警为

考虑二元假设检验问题:

其中，i=1，2，…，n，n 为雷达的部数。

在各雷达相互独立条件下，似然比T(D)为:

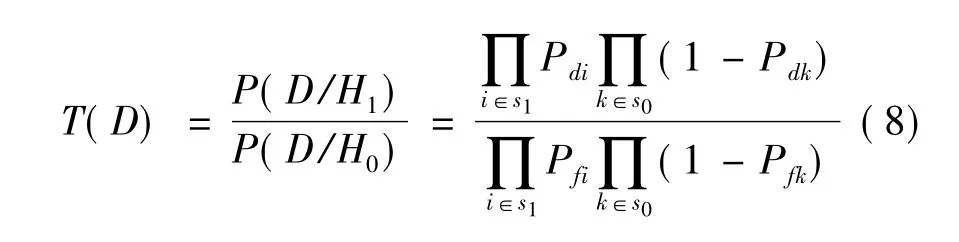
式中S1为判定目标存在的检测器组;S0为判定目标不存在的检测器组。列出所有可能的D的实现Di，1≤ i≤ N=2n，使得:

于是Neyman-Pearson融合规则检测总概率如下:

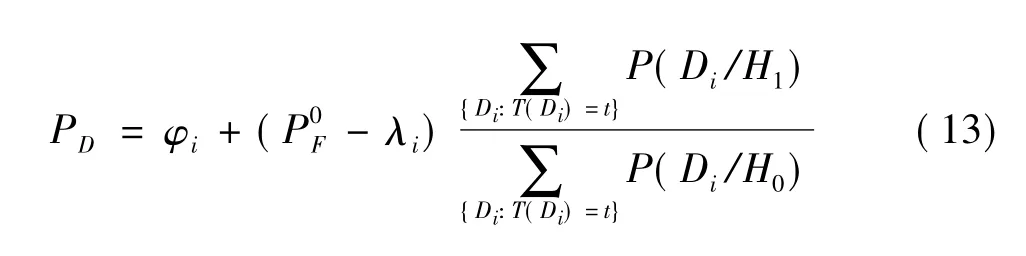
Neyman-Pearson融合规则既保持融合检测的虚警概率，又使其检测概率最大。这种最优化方式极具意义，它在提高系统检测性能的同时，又使整个系统具有恒虚警的特性。

3 仿真环境构建与结果分析

3.1 仿真环境构建

构建的仿真环境满足如下条件:假设雷达网由三部完全相同的雷达构成，其坐标分别为(0，0)m，(20000，20000)m，(0，30000)m;对雷达网实施远距离支援干扰的为两部性能完全相同，但设置参数不同的干扰机;雷达网中每部雷达天线的主瓣始终指向目标;目标模型服从起伏模型SwerlingⅠ，慢起伏，瑞利分布。雷达工作参数设置如表1所示，干扰机工作参数设置如表2所示。

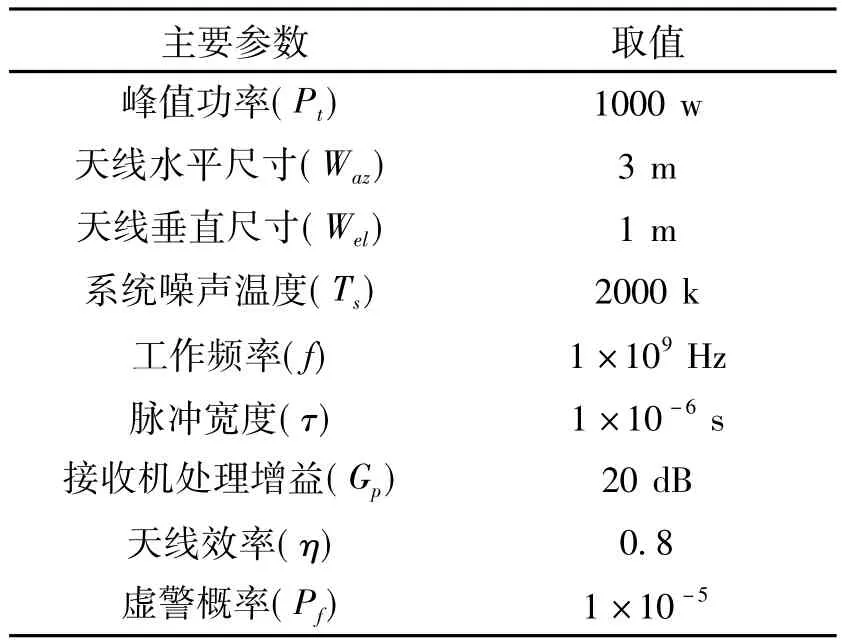
表1 雷达工作参数设置表

表2 干扰机工作参数设置表

3.2 仿真结果

a.根据构建的仿真环境，通过仿真可得出在秩K准则中的虚警总概率如表3所示。

表3 秩K融合规则中K=1、2、3时融合中心总虚警概率

b.秩K准则下雷达网检测概率分布图

图2、3、4 为 K=1、2、3 时秩 K 准则下的雷达网检测概率分布图。

c.Neyman-Pearson融合准则下雷达网检测概率分布图

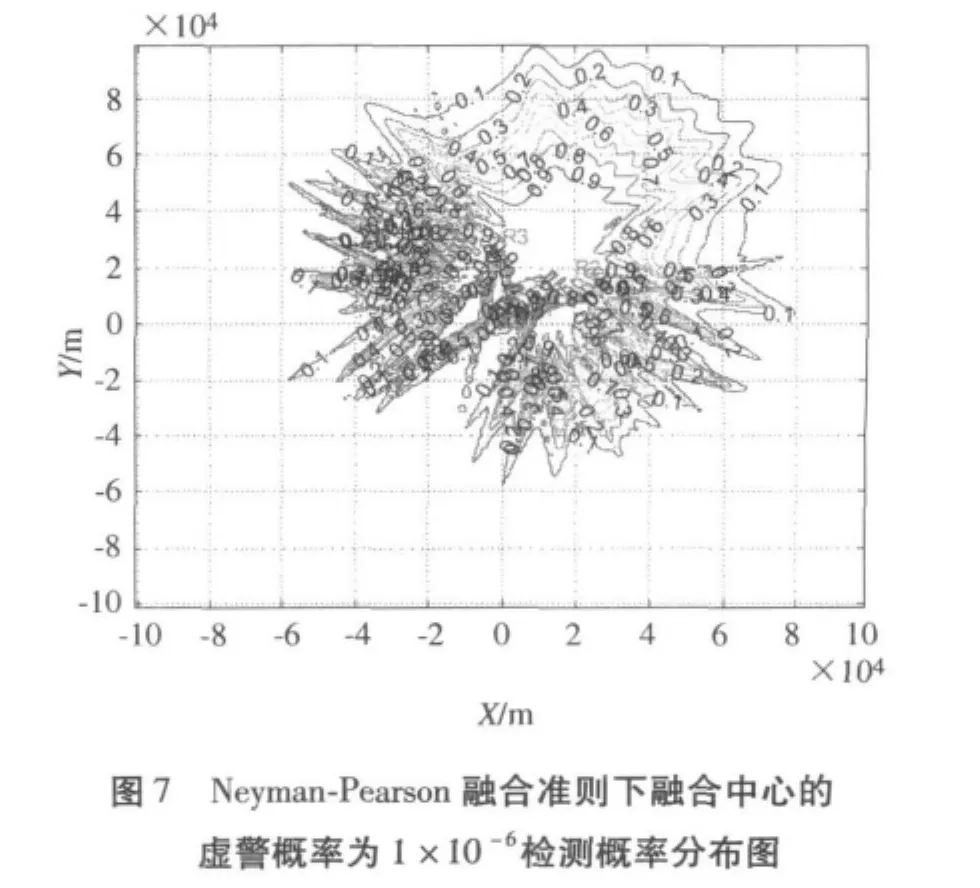
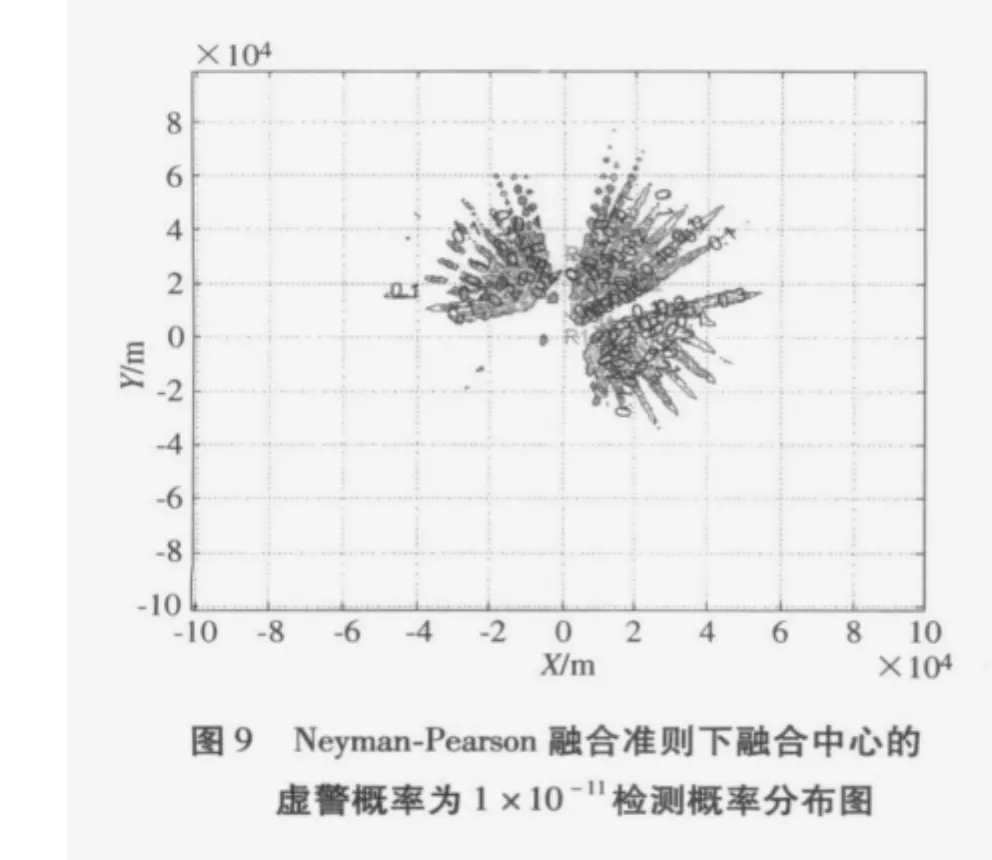
图5～9为设定融合中心的虚警概率分别为1×10－4、1 × 10－5、1 × 10－6、1 × 10－10、1 × 10－11时 Neyman-Pearson融合准则下的雷达网检测概率分布图。

3.3 结果分析

分析图2，3，4可以发现，当 K=1时，即采用“OR”准则可以较大的提高雷达网的检测概率，但融合中心的虚警概率最大，随着K值的增加，融合中心的虚警概率大幅下降，但是检测概率分布也相应大幅下降，因此，秩K必须综合考虑。

Neyman-Pearson融合准则可以提高整个雷达网的检测概率，同时使整个系统具有恒虚警的特性。在实际中可以根据雷达网在干扰中的作战需求来确定融合中心的虚警概率，从而更好的发挥雷达网的探测性能。

分析图5～9可以发现，当融合中心的虚警概率为1×10－4和1 ×10－5时 Neyman-Pearson 融合与单部雷达虚警为10－5，秩K=1准则时的检测概率分布曲线大致相当;当融合中心的虚警概率为1×10－6和1 ×10－10时 Neyman-Pearson 融合与单部雷达虚警为10－5，秩K=2准则时的检测概率分布曲线大致相当;当融合中心的虚警概率为1×10－11时Neyman-Pearson融合与单部雷达虚警为10－5，秩K=3准则时的检测概率分布曲线大致相当。

4 结束语

文中通过研究干扰条件下的检测概率分布图，分析比较了干扰下的各种融合规则，总结得出同等条件下两个融合准则间的关系和Neyman-Pearson融合准则中融合中心检测概率变化规律。在实际应用中，可以根据雷达网的不同需求确定融合中心的虚警概率，利用Neyman-Pearson融合准则来改善雷达网分布式检测性能。同时检测概率分布曲线图还可为雷达网检测性能做一个直观、全面的评估。

［1］李国君，陈国良，唐小明.基于模糊函数的双基地雷达信号检测分析［J］.火控雷达技术，2011，40(1).

［2］李圣衍，胡东，周宏宇，张浩元.雷达组网的干扰技术研究浅谈［J］.电子工程师，2006，32(11).

［3］Drakopoulos E，Lee C C.Optimum multisensor fusion of correlated local decisions.IEEE Trans on Aerospace and Elect Syst.1991，27(4):593－605.

［4］谭贤四，武文，王红，毕红葵.区域警戒雷达网优化部署研究［J］.现代雷达，2001，23(5).

［5］谭贤四，武文，王红，毕红葵.区域雷达网分布式检测性能改善方法［J］.火力与指挥控制，2001，26(4).

［6］李宏，许世军，刘诗斌.分布式雷达检测数据融合系统及性能分析［J］.现代雷达，2005，27(4).

［7］王国玉，汪连栋.雷达电子战系统数学仿真与评估［M］.北京:国防工业出版社，2004:194－207;267－278.

［8］Bassem R.Mahafza，Ph.D.Radar Systems A-nalysis and Design Using MATLAB.Chapman＆ Hall/CRC Press LLC，2000.

［9］［美］M.I.斯科尔尼克.雷达手册(第三版)［M］.北京:电子工业出版社，2010:262－279.