模拟过套管电阻率测井响应的递推矩阵方法

魏宝君，田坤，张旭，刘坤

(1.中国石油大学物理科学与技术学院，山东青岛266555;2.中国石油大学山东省高校新能源物理与材料科学重点实验室，山东青岛266555)

模拟过套管电阻率测井响应的递推矩阵方法

魏宝君1，2，田坤1，张旭1，刘坤1

(1.中国石油大学物理科学与技术学院，山东青岛266555;2.中国石油大学山东省高校新能源物理与材料科学重点实验室，山东青岛266555)

采用递推矩阵方法计算过套管电阻率测井响应的修正传输线方程，并模拟不同地层模型的测井响应，考察水泥环、电极距、套管非均匀性等因素对测井响应的影响。该方法在传输线方程系数中考虑径向含多个界面地层的影响，可以给出轴向呈层状、径向阶跃变化地层模型的电势分布，具有计算量小、易编程、无溢出等优点。模拟结果表明:递推矩阵方法具有很强的地层界面轴向分辨能力;低电导率水泥环对高电导率地层的测井响应产生更为明显的影响;径向存在多个地层界面时计算结果为径向各层电导率的综合反映;套管变薄或变厚对测井响应都有一定影响且测井异常发生在套管突变点附近;电极距对测井结果亦产生影响。

电测井;电导率;套管;传输线方程;递推矩阵方法

从20世纪30年代过套管电阻率测井被提出后，由于方法研究和工程技术上的不成熟，其后几十年一直未取得突破性进展［1-12］。20世纪90年代Kaufman发表了基于传输线方程的套管井电阻率测井近似理论模型和测量理论，奠定了过套管电阻率测井的基础并使之逐步投入商业应用［4-15］。在数值计算方面，因为金属套管电阻率和地层电阻率的差别相当大，这使原有的计算方法受到限制。虽然有限元和有限差分法被广泛应用于大地电磁场的计算中［6-20］，但是还没有被用于过套管电阻率测井响应的计算。积分方程法已经用来计算过套管电阻率测井响应，但是这方面的文献仅限于对径向均匀层状地层的测井响应进行研究［4-5］，还没有涉及到径向存在多个地层界面的情况，而且所有这些方法均无法消除系数矩阵的巨大差别。传输线方程中不同地层的系数都包含了套管的影响，系数矩阵差别不大，而且可以在不同区域的方程系数中考虑径向层状地层对测井响应的影响，形成了修正的传输线方程［12］，进而实现对轴向呈层状、径向阶跃变化地层模型测井响应的数值模拟，所以传输线法是一个很好的选择。笔者采用修正的传输线方程计算过套管电阻率测井响应，并利用递推矩阵方法［21-22］求解传输线方程组。

1 传输线方程基本理论

1.1 传输线方程理论模型

套管传输线模型如图1所示。设套管单位长度的电阻为Rc，则Rc=ρc/(2πaΔa)，其中ρc是套管电阻率，a是套管内半径，Δa是套管厚度。设套管单位长度的电导是Sc，则Sc=1/Rc。若设单位长度金属套管所对应的地层横向电阻是T(漏电电阻)，单位长度的并联导纳为Y(Y=1/T)，I为套管所载电流且与z同向，U为套管管壁到“电势无穷远点”的电势，b为“电势无穷远点”到井轴的横向距离，则有

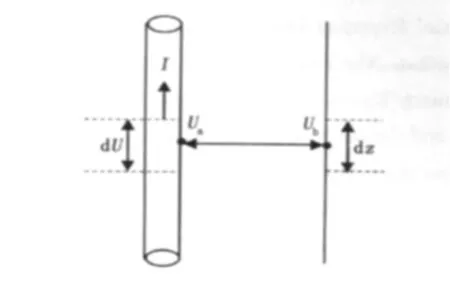
图1 套管传输线模型Fig.1 Transmission line model of casing

对于分层块状均匀地层，在均匀层块内dY/dz、dRc/dz为零，对式(1)、(2)求导可得

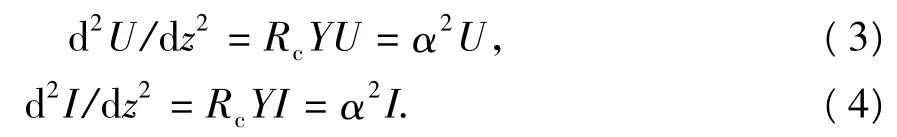
如图2，设地层在径向由m层同轴柱体组成，则单位长度套管对应的横向电阻T可由电阻定律得到

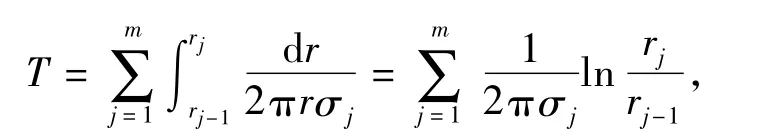
式中，σj为径向第j层地层的电导率。

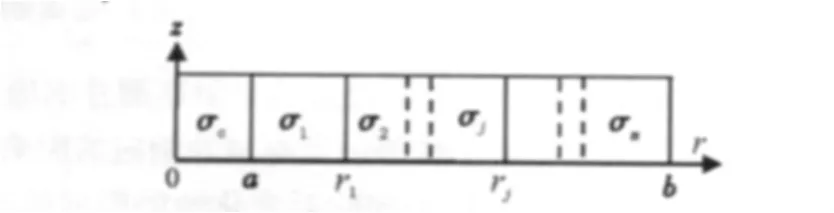
图2 径向阶跃变化地层模型Fig.2 Stair-stepped formation model in radial direction

视电阻率和视电导率公式定义［6-7］为

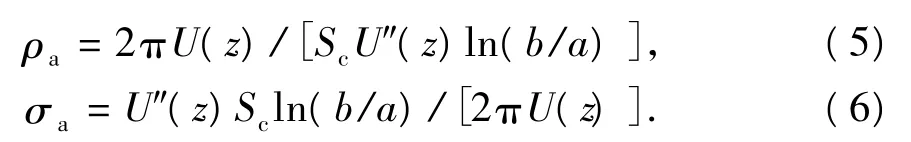
根据式(3)、(4)和边界条件可得到套管壁上的电势分布，再利用式(5)和(6)可计算出地层模型的视电阻率或视电导率。

1.2 求解传输线方程的递推矩阵方法

采用如图3所示的分层块状均匀地层模型，在柱坐标系中，地层在轴向上由n+1层组成、在径向上由同轴多层柱体组成，利用此模型可计算轴向各层的方程系数αi，i=1，2，…，n+1。图中di(i=1，2，…，n)为第i层上界面的轴向坐标，σi，j为轴向第i层、径向第j层地层的电导率。

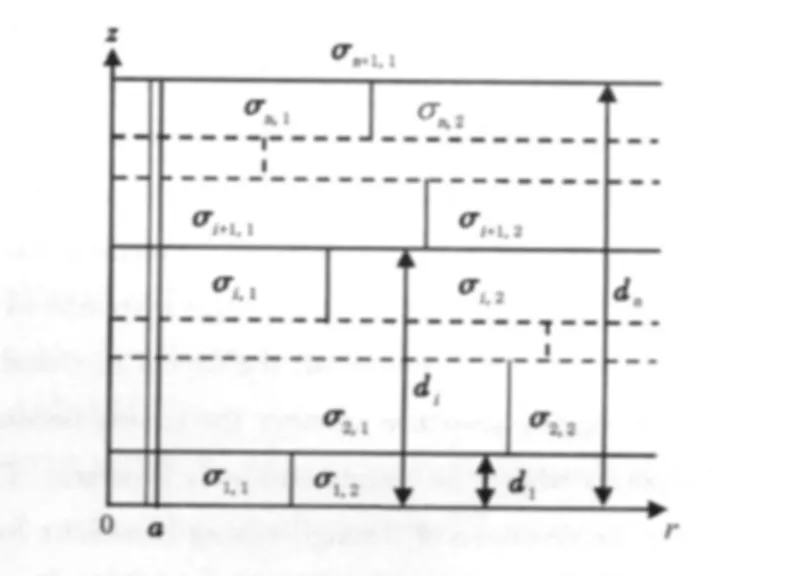
图3 过套管电阻率测井地层模型Fig.3 Formation model of through-casing resistivity logging

设在轴向第i层地层中方程(3)、(4)的解为

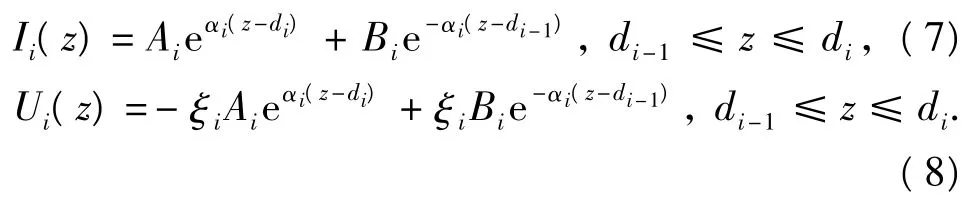
式中，Ai、Bi为待定系数;ξi=Tiαi。由边界条件可得

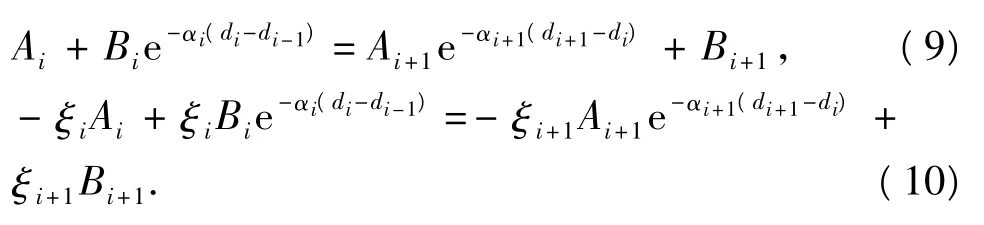
令d0=0，设电流源位于坐标原点，则I1(0)=A1e－α1d1+B1=I0，其中I0是电源电流。因为在第n+1层地层中z可以取无限远而电流有限，所以An+1=0。由这两个条件和所有边界条件可得到确定所有待定系数Ai、Bi的线性方程组。整理该方程组可得

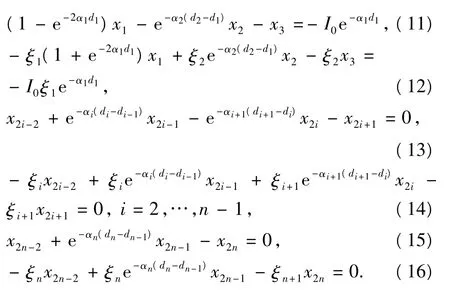
其中

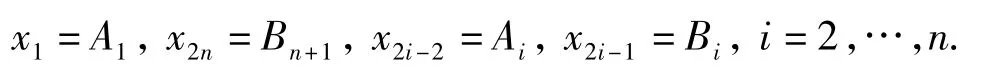
线性方程组(11)～(16)的系数组成的矩阵是稀疏带状矩阵，考虑到系数矩阵中各元素的组成特点(各行中间元素是指数衰减的)，式(11)～(16)可采用递推方法［21-22］求解。由式(11)和式(12)，用x2表示x1和x3，得

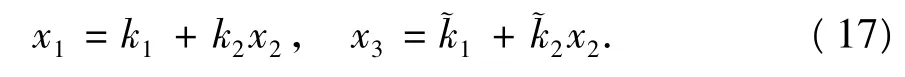
其中

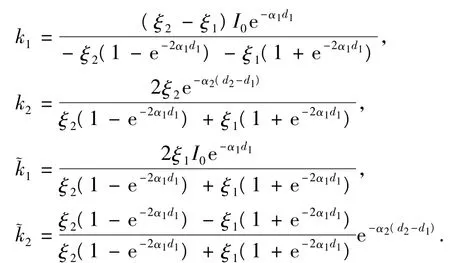
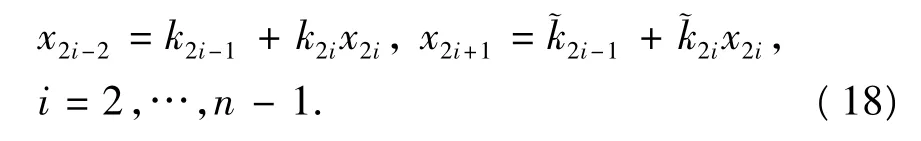
其中

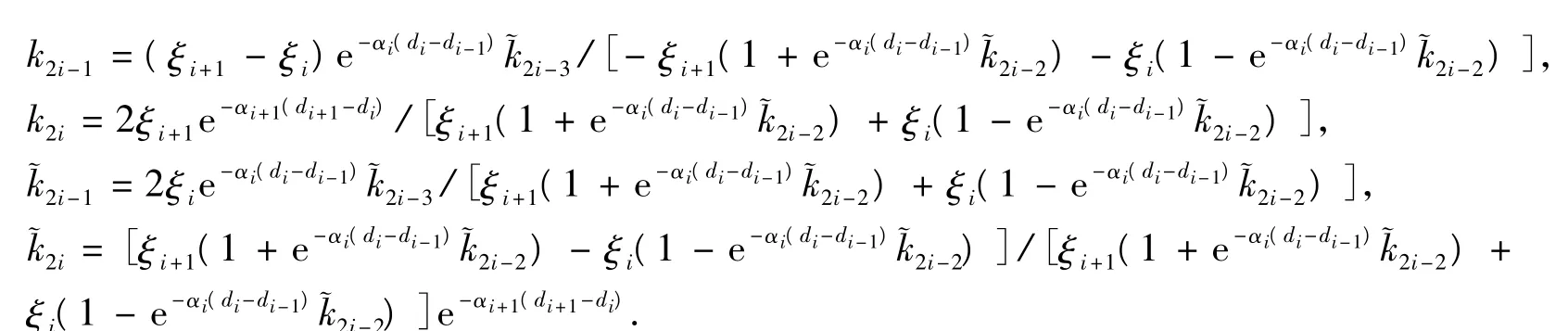
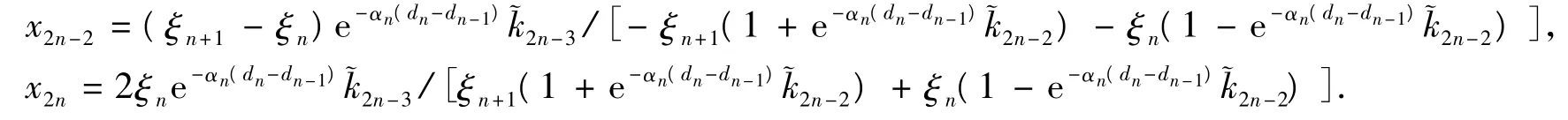
利用递推矩阵方法求解式(11)～(16)的具体步骤为:首先进行正向递推，得到系数，然后再进行逆向递推，由x2n、x2n－2经逆向递推得到x2i－2，x2i+1(i=n－1，…，2)，x3，x1。该算法在正向递推过程中仅需n次迭代，在逆向递推过程中亦仅需n次迭代，运算量为O(n)。

2 模型算例

2.1 轴向层状地层模型的响应

取仪器为三电极系，电源供电电流I0=6 A，电极距L=1.2 m，套管内半径a=0.1 m，套管厚度Δa=0.01 m，套管的电导率σc=5×106S/m。求取视电导率时用3个测量电极电势的二阶差商近似代替二阶导数实现对电势导数的计算，即U″≈ΔU/(L/2)2，其中ΔU为二阶电位差。

图4(a)为一个轴向3层地层模型的测井响应曲线，模型上、下围岩的电导率分别为3.0、1.0 S/m，中间层电导率分别取0.2、0.7、9.0、30.0 S/m，厚度为3.0 m。图4(b)是一个轴向9层地层模型的测井响应曲线，层界面轴向坐标分别为－5.6、－3.6、－2.2、－1.4、1.0、1.4、2.8、5.6 m，每层电导率分别为1.5、85.0、4.2、55.0、2.0、27.5、2.1、42.5、1.5 S/m。

由图4可以看出，在不存在水泥环且套管均匀的情况下，过套管电阻率测井响应能够比较好地反映地层的真实情况，传输线方程及其递推矩阵解法有比较好的精确性和可靠性。但是，对于薄层，其响应曲线会有较大误差，曲线分层能力较差。另外，低电导率地层的响应曲线对地层界面的敏感性也比相同厚度的高电导率地层差，确定地层界面的误差相对较大。

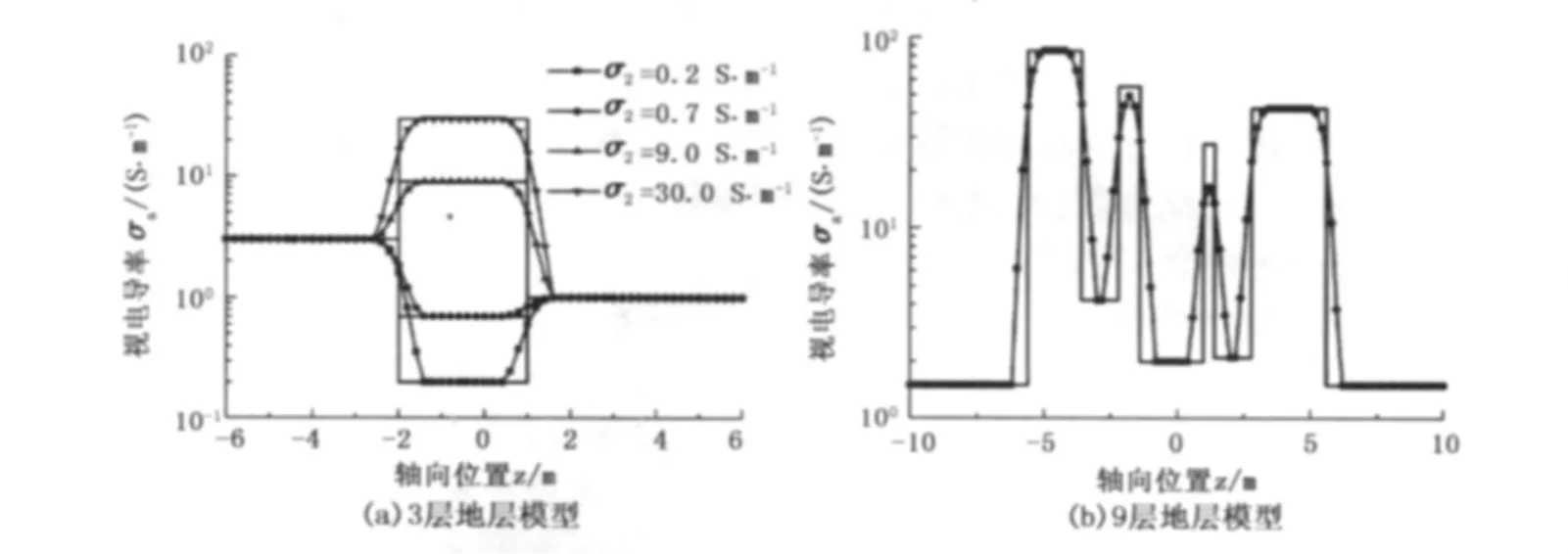
图4 3层和9层地层模型的视电导率曲线Fig.4 Apparent conductivity response of three-layer and nine-layer formation model

2.2 含水泥环层状地层的响应

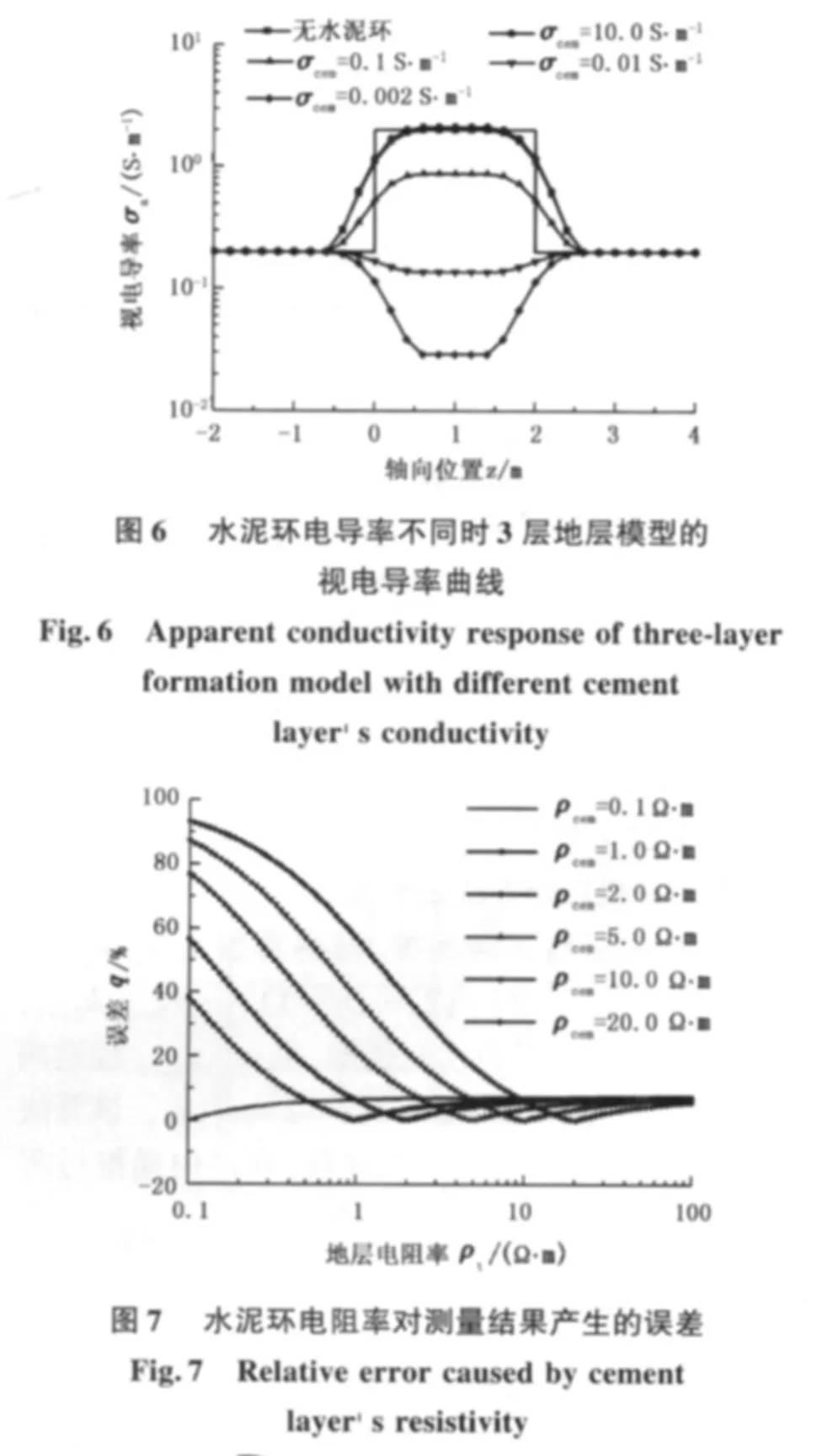
取水泥环的厚度为0.05 m、电导率σcem=0.02 S/m，图5是含水泥环7层地层模型的测井响应曲线。该模型每层地层均含有水泥环，层界面轴向坐标分别为－6、－4、－2、0、2、4 m，每层电导率分别为0.01、0.1、0.005、1、0.002、0.5、0.05 S/m。图6是一个3层地层模型的测井响应曲线，模型上下围岩的电导率均为0.2 S/m，中间地层电导率σ2=2.0 S/m，只有中间层含有水泥环且水泥环电导率可变化。由图5和图6可知，如果水泥环的电导率高于地层电导率，则其对测井响应的影响不明显。尤其是对低电导率地层，高电导率水泥环的影响可以忽略不计，但是在高电导率地层中，相对低电导率的水泥环会引起明显的测量误差。

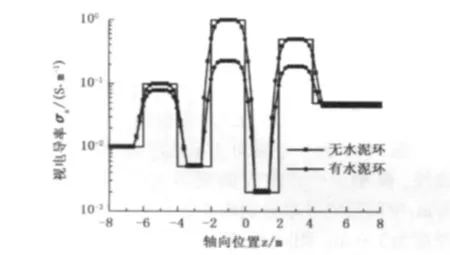
图5 7层地层模型的视电导率曲线Fig.5 Apparent conductivity response of seven-layer formation model

图7是水泥环的电阻率对仪器在具有不同电阻率地层中的测量结果产生的误差。由图7可以看出，水泥环的存在对低阻地层和高阻地层的测井响应都有影响，尤其是对低阻地层的影响更为明显，当水泥环电阻率与地层电阻率相同时误差为零。总的说来，水泥环电阻率越大，所导致的测量误差越大。

上述结论也同样体现在含侵入带地层等径向层状地层模型中。如图8所示，设地层模型在轴向上有3层，模型上下围岩的电导率均为0.2 S/m且无侵入，中间层侵入带的电导率σ2，1为10 S/m、原状地层的电导率σ2，2为1.0 S/m。由计算结果可以看出径向界面半径的变化对视电导率响应有明显的影响，且随着侵入带半径r的增大影响更加明显。

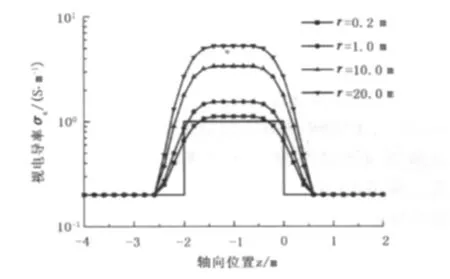
图8 径向两层地层模型的视电导率响应曲线Fig.8 Apparent conductivity response of radial two-layer formation model

2.3 轴向和径向均为多层地层时的测井响应

所采用的地层模型在轴向上除上下围岩外中间共有5个地层，这些地层在径向上也分为5层，模型上下围岩的电导率均为1.0 S/m，中间5个地层的电导率分布及径向界面半径取值如下:

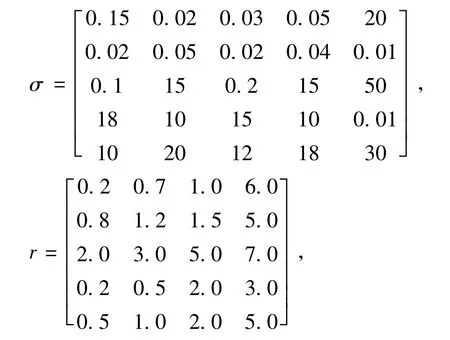
其中各元素σi，j和ri，j中的i表示轴向编号，j表示径向编号。该模型中间地层轴向第1、2层在径向上的前4层为低电导率层，径向第5层(原状地层)则分别为高电导率和低电导率层。该模型中间地层轴向第4、5层在径向上的前4层为高电导率层，径向第5层则分别为低电导率和高电导率层。该模型中间地层轴向第3层在径向上既含有高电导率地层又含有低电导率地层，而原状地层则为高电导率层。图9为该模型的原状地层电导率分布和测井响应曲线。

由图9可以看出，径向呈多层状地层模型的模拟结果并不是径向某层电导率的体现，而是径向各层电导率的综合结果。虽然径向各层电导率的分布对模拟结果有重要影响，但是测井响应曲线并不能确定径向地层界面的分布状况。另由图9也可以看出，径向低电导率层段对计算结果的影响比较大，视电导率与低电导率层段地层的电导率值更加接近，这对测井解释具有重要意义。

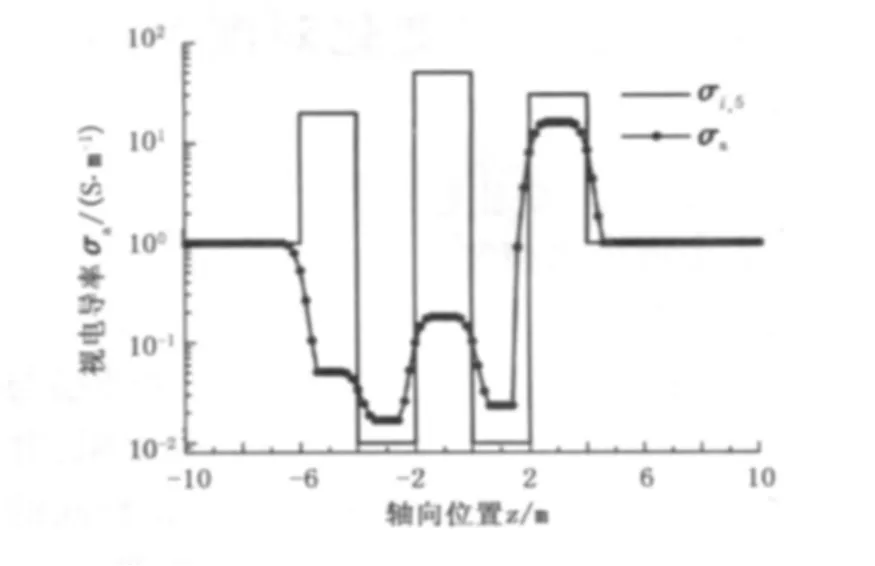
图9 轴向和径向均为多层地层模型的测井响应曲线Fig.9 Logging response of multi-layer formation model both in axial and radial direction

3 电极距对测井结果的影响

本文中采用二阶差商近似代替二阶导数以实现电势导数的计算，结合式(5)、(6)则有

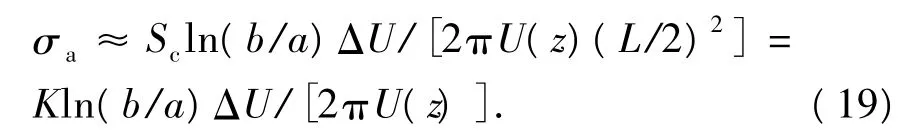
其中K=4Sc/L2，K为电极系数，该式反映了电极系数与电极距之间的关系。

图10是具有不同电极距的仪器在一个3层地层

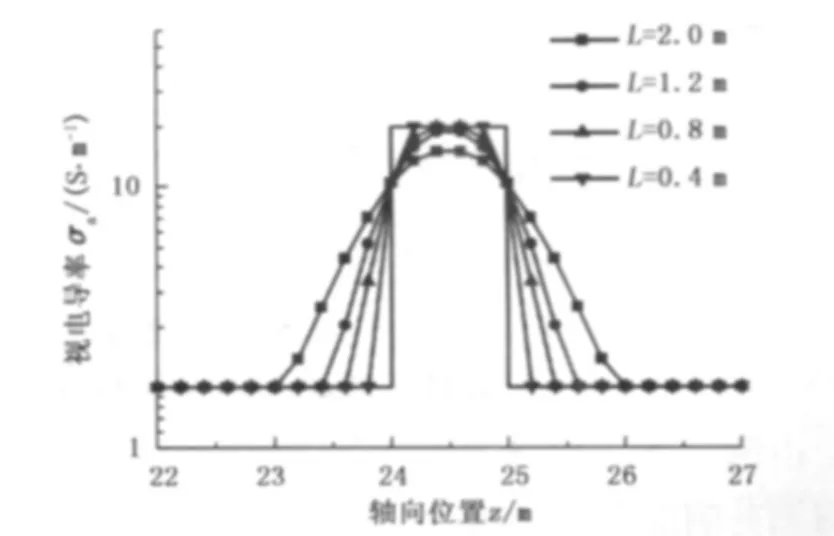
图10 电极距不同时的测井响应曲线Fig.10 Logging response for different electrode spacing

模型中的测井响应曲线。从图10可以看出，电极距越小，测井响应对地层界面的反映越灵敏，其对地层界面的分辨率也就越高。但是，随着电极距的不断减小，二阶电位差信号也会越来越微弱，对其测量也就越困难，所以在对仪器进行设计时应选择合理的电极距。由于目前测量二阶电位差信号的水平有限，现有的大多数过套管电阻率测井仪器的电极距均选择为1 m左右。如果要提高仪器对地层界面以及薄层的分辨能力，就需要研制出电极距更小的测井仪器，这有待于进一步提高测量微小电位差信号的技术水平。

4 套管的非均匀变化对测井结果的影响

套管的非均匀变化包括套管形状变化、厚度变化和接箍、腐蚀的出现等，这些变化在传输线方程中均体现在方程系数α上，并且α的差别只表现在轴向上。如对于套管腐蚀层，可以看作是腐蚀层与原来套管的并联以求取套管单位长度的总电阻，并进而求取相应的α，所以可以将方程系数α相同的地层称为一个导电层［14］。

模拟计算表明，套管的非均匀变化对视电阻率公式(5)的计算结果影响比较大，这是因为在套管单位长度电阻变化的地方会带来额外的电位差，从而影响二阶电位差的计算，而电位差信号本身微小，所以所带来的误差很可观。俄罗斯对ECOS-31-7仪器作了改进，用上下两个供电电极分别供电，仪器尺寸及电极排列顺序为:A11.3M10.5N0.5M21.3A2(m)，并采用如下视电阻率公式［15］:

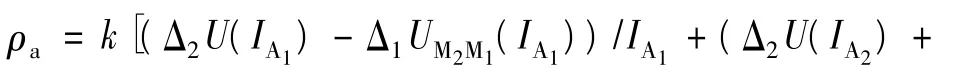
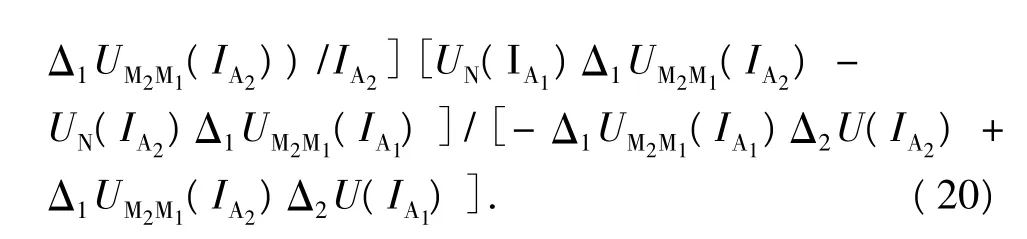
式中，下标为电极标号;A1和A2为供电电极;M1、N、M2为测量电极;IA1、IA2分别为A1和A2供电时的供电电流;Δ1UM2M1为M1、M2之间的一阶电位差;UN为电极N的电位;Δ2U为二阶电位差。在套管均匀的条件下，式(20)和式(5)、(6)计算结果一致，当出现套管非均匀变化时，式(20)可在很大程度上抵消误差，从而较大幅度地压制视电阻率曲线的异常跳跃。采用式(20)来计算视电阻率，主要考察由于套管接箍的存在引起套管厚度增加和由于套管的损伤引起套管变薄这两种情况对测井响应的影响。计算时仪器和套管参数取值如下:电极距L=1.0 m，供电电流I0=6 A，套管电导率σc=5×106S/m，套管内半径a=0.0635 m，套管厚度Δa=0.00772 m。

图11(a)是存在套管接箍时的过套管电阻率测井响应曲线，套管接箍位于20～20.15 m处，长度为0.15 m，其电导率与套管的非接箍部分一致，厚度为套管厚度的两倍，地层电阻率的取值为10 Ω·m。图11(b)是含有套管变薄段的过套管电阻率测井响应曲线，变薄部分的厚度为0.00386 m，变薄部分的位置及长度同图11(a)。

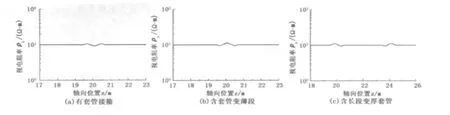
图11 套管厚度的非均匀变化对测井结果的影响Fig.11 Effect of nonuniform variation of casing thickeness on logging results

由图11(a)和(b)可以看出，套管变厚或变薄均对测井响应产生影响，但影响不是很大，基本不会影响正常读数。虽然套管异常段的长度只有0.15 m，但视电阻率曲线的影响范围大于1 m，这是由电极距引起的，因为3个测量电极只要有一个进入异常段，视电阻率曲线就会出现异常。对比图11(a)和(b)还可看出，套管变厚或变薄造成的曲线弯曲方向相反。

图11(c)是含有长段变厚套管的测井响应曲线，异常段套管厚度为0.013 m，长度为4 m，位于20～24 m处。可以看出，在套管厚度正常的区域和套管变厚区域测井曲线能较好地反映地层电阻率。套管厚度变化的影响只出现在套管单位长度电阻突变端点附近，且曲线异常段长度等于测量电极的电极距。这是因为只有当3个测量电极不在同厚度的套管上时视电阻率曲线才会出现异常，且异常段的起点是第一个测量电极开始进入套管厚度变化区，终点是3个测量电极刚刚全部进入套管厚度变化区。

5 结论

(1)采用递推矩阵方法计算过套管电阻率测井响应的修正传输线方程，具有计算量小、易编程、无溢出等优点，可有效求解过套管电阻率测井在轴向、径向均为层状地层的响应。

(2)过套管电阻率测井响应能够比较好地反映地层电阻率分布的真实情况。低电导率水泥环对高电导率地层中的测井响应产生更为明显的影响，而高电导率水泥环的影响不是很明显。径向存在多个地层界面时的视电导率是径向各层电导率的综合反映，其中低电导率层段对响应的影响较大。套管单位长度电阻的变化会对测井响应产生一定影响，但不影响正常读数。

［1］VAIL W B.Methods and apparatus for measurement of electronic properties geological formation through borehole casing:US，4882542［P］.1989-11-21.

［2］VAIL W B.Methods and apparatus for measurement of the resistivity of geological formation from within cased well in presence of acoustical magnetic energy sources:US，5043669［P］.1991-08-27.

［3］VAIL W B.Measuring resistivity changes from within a first cased well to fluids injected into oil bearing geological formation from a second cased well while passing electrical current between the two cased well:US，5187440［P］.1993-02-16.

［4］SCHENKEL C J，MORRISION H F.Effects of well casing on potential field measurements using downhole current sources［J］.Geophysical Prospecting，1990，38(3):663-686.

［5］谢树棋，储昭坦，李克沛，等.套管电阻率测井方法研究［J］.测井技术，1990，23(5):338-343.XIE Shu-qi，CHU Zhao-tan，LI Ke-pei，et al.On methodology of resistivity logging through casing［J］.Well Logging Technology，1999，23(5):338-343.

［6］KAUFMAN A A.The electrical field in a borehole with a casing［J］.Geophysics，1990，55(1):29-38.

［7］KAUFMAN A A，WIGHTMAN W E.A transmissionline model for electrical logging through casing［J］.Geophysics，1992，58(12):1739-1747.

［8］SCHENKEL C J，MORRISION H F.Electrical resistivity measurement through metal casing［J］.Geophysics，1994，59(4):1072-1082.

［9］尤建军，张超谟，陈详，等.CHFR测井原理及影响因素研究［J］.地球物理学进展，2005，20(3):780-785.YOU Jian-jun，ZHANG Chao-mo，CHEN Xiang，et al.The principle of CHFR logging and its influence factors［J］.Progress in Geophysics，2005，20(3):780-785.

［10］高杰，刘福平，包德洲，等.过套管电阻率测井方法研究［J］.测井技术，2007，31(3):229-232.GAO Jie，LIU Fu-ping，BAO De-zhou，et al.Study on through-casing resistivity logging［J］.Well Logging Technology，2007，31(3):229-232.

［11］张金钟.水泥环对套管井电阻率测井的影响［J］.测井技术，1995，19(6):406-410.ZHANG Jin-zhong.The effect of cement annulus on resistivity log in cased hole［J］.Well Logging Technology，1995，19(6):406-410.

［12］刘福平，高杰，孙宝佃，等.实际井眼条件下过套管电阻率测井响应的传输线方程正演算法［J］.地球物理学报，2007，50(6):1905-1913.LIU Fu-ping，GAO Jie，SUN Bao-dian，et al.Forward calculation of the resistivity logging response through casing by transmission line equation for multi-layer formations［J］.Chinese J Geophys，2007，50(6):1905-1913.

［13］刘胜建，张明峰.过套管电阻率测井应用探讨［J］.油气井测试，2003，12(4):23-25.LIU Sheng-jian，ZHANG Ming-feng.The discuss of appliance of resistance rate for over-thimble［J］.Oil and Gas Well Test，2003，12(4):23-25.

［14］高杰，刘福平，包德洲，等.非均匀套管井中的过套管电阻率测井响应［J］.地球物理学报，2008，51(4):1255-1261.GAO Jie，LIU Fu-ping，BAO De-zhou，et al.Responses simulation of through-casing resistivity logging in heterogeneous-casing wells［J］.Chinese J Geophys，2008，51(4):1255-1261.

［15］王正国.俄罗斯过套管电阻率测井研究及应用［J］.测井技术，2009，33(4):374-378.WANG Zheng-guo.Study on the Russian through casing resistivity logging and its application［J］.Well Logging Technology，2009，33(4):374-378.

［16］魏宝君，张庚骥.三维井间电磁场的正反演计算［J］.地球物理学报，2002，45(5):735-743.WEI Bao-jun，ZHANG Geng-ji.Forward modeling and inversion of 3-D crosshole electromagnetic fields［J］.Chinese J Geophys，2002，45(5):735-743.

［17］曾文冲，赵文杰，臧德福.井间电磁成像系统应用研究［J］.地球物理学报，2001，44(3):411-420.ZENG Wen-chong，ZHAO Wen-jie，ZANG De-fu.Application research of crosshole electromagnetic tomography［J］.Chinese J Geophys，2001，44(3):411-420.

［18］汪功礼，张庚骥，崔锋修，等.三维感应测井响应的交错网格有限差分法［J］.地球物理学报，2003，46(4):561-567.WANG Gong-li，ZHANG Geng-ji，CUI Feng-xiu，et al.Application of staggered grid finite differrence to the computation of 3-D induction logging response［J］.Chinese J Geophys，2003，46(4):561-567.

［19］熊斌，罗延钟.电导率分块均匀瞬变电磁2.5维有限元数值模拟［J］.地球物理学报，2006，49(2):590-597.XIONG Bin，LUO Yan-zhong.Finite element modeling of 2.5-D TEM with block homogeneous［J］.Chinese J Geophys，2006，49(2):590-597.

［20］魏宝君.一种新型随钻电阻率测井仪器的响应和刻度［J］.地球物理学报，2007，50(2):632-641.WEI Bao-jun.Response and calibration of a new logging-while-drilling resistivity tool［J］.Chinese J Geophys，2007，50(2):632-641.

［21］WEI B J，ZHANG G J，LIU Q H.Recursive algorithm and accurate computation of dyadic Green's functions for stratified uniaxial anisotropic media［J］.Science in China(Series F)，2008，51(1):63-80.

［22］田坤.过套管电阻率测井响应的计算方法研究［D］.中国石油大学物理科学与技术学院，2010.TIAN Kun.The research on computing method of through-casing resistivity logging response［D］.College of Physical Science and Technology in China University of Petroleum，2010.

(编辑 修荣荣)

Recursive matrix method for simulating response of through-casing resistivity logging

WEI Bao-jun1，2，TIAN Kun1，ZHANG Xu1，LIU Kun1

(1.College of Physical Science and Technology in China University of Petroleum，Qingdao 266555，China;2.Key Laboratory of New Energy Physics＆Material Science in Universities of Shandong，China University of Petroleum，Qingdao 266555，China)

A modified transmission line equation(MTLE)for simulating the response of through-casing resistivity logging was computed by a recursive matrix method.The response of different formation models was simulated by the method，and the influence of such factors as cement layer，electrode spacing and heterogeneous casing was analyzed by the method.The influence of formation with multiple boundaries in radial direction was included in the coefficients of the transmission line equation，so the distribution of potential can be given for formation models which are layered in axial-direction and stairstepped in radial direction.The method has the virtue of little computational amount，convenient programming and no overflow.The simulation results show that the method has a high resolution of axial formation boundaries.The low-conductivity cement layer has a great influence on the response in high-conductivity formation.The computed apparent conductivity is a composition of conductivities of all the layers in radial direction as there are many layers in this direction.It has some influence on the logging response whether the casing becomes thinner or thicker，and the abnormality of logging response appears near the points where the casing suddenly changes.The simulation results also show that the electrode spacing has some influence on the response of through-casing resistivity logging.

electric logging;electric conductivity;casing;transmission line equation;recursive matrix method

P 631.9

A

10.3969/j.issn.1673-5005.2011.06.009

2011－02－08

教育部新世纪优秀人才支持计划项目(NCET-10-0767);中央高校基本科研业务费专项资金项目(10CX05006A)

魏宝君(1969－)，男(汉族)，山东临沂人，教授，博士，研究方向为应用地球物理和电磁场理论方法。

1673-5005(2011)06-0059-07