海洋电磁勘探中空气波相互作用机制和水深影响分析

沈金松，詹林森，王鹏飞，马超，连福明

(1.中国石油大学地球物理与信息工程学院，北京102249;2.中国石油大学油气资源与探测国家重点实验室，北京102249;3.中国石油大学中国石油集团公司物探重点实验室，北京102249)

海洋电磁勘探中空气波相互作用机制和水深影响分析

沈金松1，2，3，詹林森1，王鹏飞1，马超1，连福明1

(1.中国石油大学地球物理与信息工程学院，北京102249;2.中国石油大学油气资源与探测国家重点实验室，北京102249;3.中国石油大学中国石油集团公司物探重点实验室，北京102249)

基于一维层状介质的电磁位和电磁场分析，采用电磁场的模式分解理论建立空气、海水层和海底地层之间的电磁场相互作用关系。以假想无限水深模型和五层介质模型为基础，导出水平电偶极子(HED)的横电(TE)和横磁(TM)模式的电磁场数学关系，分析空气波占优的临界偏移距随水深和海底地层电导率的变化规律，指出前人定义的300 m水深作为浅水域和深水域分界深度的缺陷。以电磁响应理论为基础，讨论空气波与其他介质层相互作用强耦合特征，考察电磁响应水平分量与垂直分量受空气层相互作用影响的差异和横电与横磁模式受空气波影响的不同特征。结果表明:空气波是电磁波在空气层、海水层和海底地层的相互耦合作用下产生的散射波场，且在TM和TE两种模式上表现出较大差异;电场垂直分量只有TM模式的贡献，受空气波影响小，测量垂直电场分量将有利于减弱空气波的影响;要根据海底电导率、水深和偏移距的关系确定空气占优的临界偏移距，不能笼统定义深水和浅水的界限。

电磁勘探;电磁场;电磁波;电导率;空气波相互作用;模式分解;层状介质模型

海洋可控源电磁勘探(MCSEM)方法已被广泛用于深水域油气勘探［1－3］，并取得巨大发展［4－6］，而其真正用于深部海洋油气勘探仅有几年时间［4－5］。由于该方法中电磁源的激发频率较低，电磁场传播以散射场为主，前人建立的一些基于波场传播的海洋电磁数据处理方法在实际应用中显现出诸多不适应性［7－8］，如前人提出的水深大于300 m作为深水域处理的概念［9－10］，目前海洋电磁勘探相关文献资料所提到的“空气波”概念［4－5，7－8］，以及前人基于“空气波”的波动性质提出的上行波和下行波分离压制空气波的方法等［7－8］。尤其在浅水域中，强度较大的空气波信号淹没了来自海底地层的有效信号，造成“可控源海洋电磁勘探在浅水域无效”的传统认识［11］使MCSEM实际应用受到了挑战。海洋电磁勘探中“空气波”的影响最早是由Chave和Cox［3］描述的，目前都是作为干扰信号加以剔除。该概念［3，12］是将电磁场能量在导电介质中的传播与弹性波传播作类比而提出的，且基于“空气波”影响的分析，前人提出了水深300 m作为“浅水域和深水域”的界限［13－15］，开展了电磁响应特征和灵敏度的系列研究［14，16］。Sasaki等［17］和刘长胜等［18］分别以水深300 m作为“浅水域和深水域”的界限，分析了浅部异常、水深和空气波对电磁响应的影响。Andreis和Lucy［13］利用一维模型分析了CSEM应用于浅水域勘探的物理机制，指出了空气波与地层有效信号的复杂耦合关系，但对浅水域CSEM信号的传播特征和空气波的作用机制仍然缺乏全面定量的分析。笔者在Andreis和Lucy［13］的基础上，基于电磁场的模式分解理论将HED激发的电磁场分解为横电(TE)和横磁(TM)模式，导出两种模式的电磁场数学关系，分析海底接收信号中空气波、海水层与海底地层电磁场的相互作用，考察横电(TE)和横磁(TM)模式电磁场中空气波相互作用的差异和空气波与海水层、海底地层信号之间的耦合机制。

1 电磁场基本方程和TE、TM模式定义

存在激发源的情况下频率域电磁场的Maxwell方程［19］可以表示为

对于可控源海洋电磁测量中的水平电偶极子，可将方程(1)中的电场和磁场强度分解为TE和TM两种模式，即

式中，ETE和ETM、HTE和HTM分别表示TE和TM模式电场和磁场强度。

由文献［19］，TE和TM两种模式的电磁场可用Schelkunoff定义的两个矢量位函数A和F表示为

其中的位函数A和F满足如下非均匀Helmholtz方程:

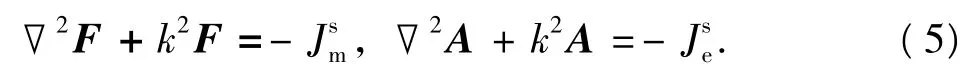
在均匀介质中，利用直角坐标系下二维傅里叶变换求解HED激发的位函数方程(5)，可以得到变换域电磁位函数在柱坐标下的解［19］:

其中

式中，I为电流强度;ds为电偶极子的长度;kx和ky分别为直角坐标系下二维傅里叶变换x、y方向的波数;ρ为柱坐标中的径向距离;J0(λρ)为零阶贝塞尔函数。将式(6)和(7)代入式(3)和(4)即得到柱坐标系下电磁场横电和横磁两种模式［19］的解。

2 一维层状介质中电磁场的TE和TM模式

2.1 有限厚海水五层介质中TM和TE模式电磁位函数

对于有限厚海水层和海底多层的情况，也可用上面的方法导出相应的位函数和场函数关系。如图1所示，以海底作为z=0的坐标平面，源处于海底以上h处，海水层厚为H2，则空气、海水和海底地层的5层介质中TM模式的位函数形式解可表示为

图1 五层介质模型Fig.1 Five-layer model

同理，对TE模式，空气、海水和3个海底地层中的位函数有

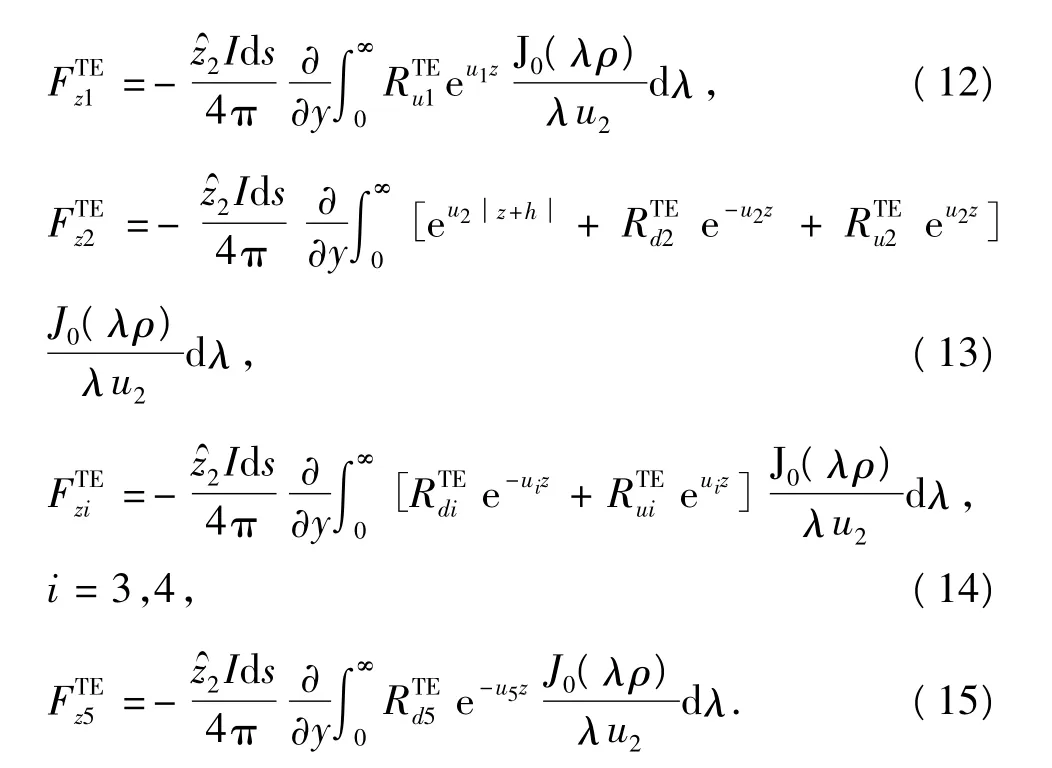
设坐标原点位于海水与海底地层的交界面，利用两种模式的电场和磁场切向分量连续交界面条件经过冗长的推导，可得TM模式波的上行、下行波传播系数:

其中

对应的TE模式波的上行、下行波传播系数为

其中

2.2 海水层中的电磁场关系

由TM和TE模式的电磁位函数关系式(8)～(11)和式(12)～(15)可得海水层中电磁场表达式［19］为

其中

其中

3 空气界面、海水层和3个海底地层相互耦合作用对海底电磁响应的影响

为更好地分析源信号与空气界面、海水层和海底地层的相互作用，以五层介质地层模型的电磁场关系为例开展空气波影响的分析。由五层介质中海水层的TM和TE模式电磁场响应整理得到

其中

其中

需要指出的是:在TM和TE模式位函数中，PTM(u2，z)和QTM(u2，z)定义的第一个大括号中的三项分别是源项、海底及以下的3个界面、单个界面和双界面作用项，第二个大括号中的三项分别是海水与空气界面与源项、海底及以下的3个界面、单个界面和双界面耦合作用项，分母项CTM和CTE中包含4个界面传播系数的耦合;PTM(u2，z)和QTM(u2，z)定义的第二个大括号中的第一项即为经典的“空气波”，它只占空气与其他几层介质相互作用的一部分。因此，只是利用上行波和下行波分离的方法只可能将第二个括号中第一项的空气作用压制，且由于分母上空气波与有效波的耦合作用，即使在压制经典的空气波时，也将损失部分有效信号。

另一方面，从式(18)和(19)的电磁场响应关系可以看到，由于空气电导率σ1→0时，，因此海水层中的TM模式电磁信号在海水和空气界面上会发生相位翻转，返回海水层，不会向空气层中透射，而对TE模式，且随海水电导率和横向空间波数发生变化，对于给定海水条件下，地层电性参数不同，出现空气波在总场中占优势的临界偏移距也发生变化。在实际资料处理中，由于地层的电性参数未知，无论采用何种分解方法，都难以将空气波的影响分离和消除。因此，对于TE模式中海水－空气界面与其他界面的相互作用的影响，只有通过海底地层的“电导率建模”估计空气波占优的临界偏移距，利用空气波影响小的数据进行处理解释。

4 不同电磁场分量的响应模拟与空气波影响分析

在进行CSEM勘探测量时，HED源位于测线上方，设电偶极子轴线方向和测线方向平行，接收器沿测线布置，通过测量不同偏移距处电磁场响应的差异来判断海底是否存在油气或水合物等高阻目标。目前大多数实际勘探和研究工作将300 m作为深海和浅海的分界线，而且MCSEM的应用实例也主要限于深海环境油气储层的探测。在浅水域环境下，MCSEM探测技术的探测能力以及水深小到什么程度来自海底高阻地层的电磁场异常会消失，目前定量研究结果不多［20－22］。因此，基于模式分解电磁场关系和多层介质地电模型，分别考察空气波对不同电磁场分量的影响。模拟计算采用图1所示的五层模型。源距海底高度为25 m，激发频率f=0.1～1 Hz，接收器间隔x=250 m，海水电导率σ0=3.33 S/m，海水层厚度H=30 m～∝，背景介质电导率σ1=0.5 S/m，高阻目标层σ2=0.01 S/m，埋深1000 m，厚度100 m。

4.1 空气波对不同电磁场分量的影响

尽管理论分析采用模式分解的电磁场关系，在实际勘探中接收器记录的电磁场均是两种模式叠加场，为了使数值模拟结果得到的认识能用于实际电磁测量数据的分析，以下给出的模拟结果均是两种模式的叠加场。相对介电常数25、激发频率为0.25 Hz、源距海底高度25 m、接收器置于海底情况下，不同海水深度下磁场Hy分量的幅度和相位模拟结果见图2。由图可见，在半对数刻度图上，无限厚海水层对应的磁场幅度随偏移距增大表现出近似线性衰减的特征，这一特征反映了均匀海底地层中电磁场的扩散特征。在50、100、150、300和500 m水深上，幅度曲线在空气波占优的临界偏移距以内与无限厚水深的电磁响应特征相似，而在相应的临界偏移距以外，幅度曲线斜率出现急剧变化，相位曲线出现平直段，反映了空气波淹没有效信号的临界位置。同时，也注意到，大于300 m和小于300 m水深的幅度和相位响应曲线存在较大差异，300 m及更浅的3个幅度响应基本相似，它们的相位差也不大，这就是目前海洋电磁勘探中大多选择300 m作为深水和浅水的分界标志的原因。

不同海水深度下电场Ex分量的幅度和相位模拟结果见图3(其他条件同图2)。与磁场Hy相似，在半对数刻度图上，无限厚海水层对应的磁场幅度随偏移距增大表现出近似线性衰减的特征，而在5个水深上，幅度曲线在空气波占优的临界偏移距以内与无限厚水深的电磁响应特征相似，且在对应的临界偏移距以外，幅度曲线斜率出现急剧变化。相位曲线出现平直段也反映了空气波淹没有效信号的临界位置。在大于300 m和小于300 m水深的幅度和相位响应曲线上，也存在以300 m为分界的特征差异。

图3 不同海水深度时Ex分量的幅度和相位响应Fig.3 Amplitude and phase response of Excomponent in different sea water depths

电场Ez分量在不同海水深度时的幅度和相位响应见图4。与两个水平电磁场分量的特征不同，电场Ez分量在所模拟的7个水深上，幅度的对数与偏移距都表现出线性衰减的趋势，但随偏移距增大，幅度曲线也出现分离，即水深变小曲线斜率增大。对于相位曲线，随海水深度变浅与无限水深相比，也只是出现微弱的相位移。因此，Ez分量受海水深度变浅引起的空气波影响较小。接收电场的垂直分量可以减弱空气波的影响。应当注意的是，除无穷水深外的其他深度上，幅度曲线仍在大偏移距上存在幅度曲线斜率的变化，表明即使电场的垂直分量也受到空气波的影响。

分析空气波影响的模拟结果时需要注意两个关键点:①在水深小于300 m的浅水域，即使在小偏移距上，电磁场的幅度和相位值与无限水深结果存在差异，电磁信号与空气的相互作用在所有偏移距上都有影响，并不限于大于临界偏移距的范围，在小于临界偏移距时，地层有效信号占优而掩盖了空气波的影响。②在所有偏移距上，包括空气波开始出现的临界偏移距以外的范围，所测得的电磁信号均与海底地层电性结构相关。尽管幅度曲线近似直线，实际上斜率仍存在微小变化，而相位曲线平坦，其梯度也没有减为零，即实际记录的电磁场相速度仍然是有限的且与海底地层电阻率相关。

图4 不同海水深度时Ez分量的幅度和相位响应Fig.4 Amplitude and phase of Ezcomponent in different sea water depths

4.2 空气波占优的临界偏移距与海底地层电导率的关系

实际测量发现，对于水深大于300 m的水域，也出现了明显的空气波的影响，传统的以300 m水深作为深水域和浅水域分界的认识受到了挑战。由电磁场关系可知，空气波与海水层、海底地层是高度耦合的，除与海水深度有关外，还与海底地层的电导率分布密切相关。因此，有必要用数值模拟方法定量考察水层和海底地层电导率对空气波占优的临界偏移距的影响。设计了3个海底地层电导率模型，分别计算不同海水深度时，空气波占优的临界偏移距的变化规律。

激发频率为0.25 Hz、源距海底高度25 m、接收器置于海底、海底背景电导率0.2 S/m情况下，磁场Hy和电场Ex分量在不同海水深度的幅度响应见图5。由图5(a)可知，对于磁场Hy分量，在海底较为高阻的情况下，5 km水深以上，在通常的25 km偏移距以内，可以不考虑空气波影响。随海水深度变浅，远偏移距接收器的信号开始受空气波影响。在300 m水深时，7 km以外的偏移距上都需要考虑空气波的影响。由图5(b)知，电场Ex分量与磁场Hy分量相比，受空气波影响的临界偏移距更大些，在300 m水深时，9 km以外的偏移距上都需要考虑空气波的影响，但5 km水深时空气波占优的临界偏移距相当。

图5 背景电导率为0.2 S/m时磁场Hy和电场Ex分量在不同海水深度的幅度响应Fig.5 Amplitude response of Hyand Excomponent in different sea water depth for background electric conductivity of 0.2 S/m

海底背景电导率1.0 S/m条件下磁场Hy和电场Ex分量在不同海水深度的幅度响应见图6。由图6(a)看到，对于磁场Hy分量，在该电导率条件下，即使是1 km水深，也会在22 km偏移距上出现空气波占优，其他几个水深的空气波占优的临界偏移距变小。图6(b)的电场Ex分量也出现了与磁场Hy分量相类似的空气波分布特征。

海底背景电导率2.0 S/m条件下磁场Hy和电场Ex分量在不同海水深度的幅度响应见图7。由图7(a)看到，对于磁场Hy分量，在该电导率条件下，即使是10 km水深，也会在15 km偏移距上出现空气波占优，其他几个水深的空气波占优的临界偏移距变小。图7(b)的电场Ex分量也出现了与磁场Hy分量相类似的空气波分布特征。

对比图6、图7可知，随海底地层的背景电导率增大，空气波占优的临界偏移距变小，因此在实际测量中需要根据背景电导率确定空气波校正的临界偏移距。

图6 背景电导率1.0 S/m时磁场Hy和电场Ex分量在不同海水深度的幅度响应Fig.6 Amplitude response of Hyand Excomponent in different sea water depth for background electric conductivity of 1.0 S/m

图7 背景电导率为2.0 S/m时磁场Hy和电场Ex分量在不同海水深度的幅度响应Fig.7 Amplitude of Hyand Excomponent in different sea water depth for background electric conductivity of 2.0 S/m

5 结束语

基于电磁场的模式分解理论和一维水平层状模型，导出了海洋电磁勘探中横电和横磁两类响应模式的电磁位和电磁场关系。基于TE和TM电磁波模式分解的理论分析可知，空气波是非常复杂的电磁散射现象，它是电磁波在空气层、海水层和海底地层的相互耦合作用下产生的散射波场，与海底地层高度耦合，前人提出的上行波和下行波分离的方法难以较好地分离空气波信号;仿照地震波传播模式定义的经典“空气波”信号只是电磁波在空气层、海水层和海底地层的相互耦合作用下产生的散射波场的一部分，即使这一部分的空气波在压制过程中也损失了有效信号;由电偶极子源激发产生的电磁波与海水－空气界面作用时，在TM和TE两种模式上表现出较大差异。在其他参数相同的情况下，电磁场的水平分量受空气波影响严重，而电场垂直分量只有横磁模式的贡献，受空气波影响小，测量垂直电场分量将有利于减弱空气波的影响。在海洋电磁实际勘探中，目前以300 m水深作为深水域和浅水域界限的认识与空气波影响规律存在矛盾，对电磁数据进行实际处理时，需要根据海底电导率、水深和偏移距的关系，确定空气占优的临界偏移距，而不能笼统地定义深水和浅水的界限。

［1］YOUNG P，COX C S.Electromagnetic active source sounding near the East Pacific Rise［J］.Geophysical Research Letters，1981，8:1043－1046.

［2］CONSTABLE S，SRNKA L J.An introduction to marine controlled source electromagnetic methods for hydrocarbon exploration［J］.Geophysics，2007，72(2):WA3－WA12.

［3］CHAVE A D，COX C S.Controlled electromagnetic sources for measuring electrical conductivity beneath the oceans I:forward problem and model study［J］.Journal of Geophysical Research，1982，87:5327－5338.

［4］EIDESMO T，ELLINGSRUD S，MACGREGOR L M，et al.Sea bed logging(SBL):a new method for remote and direct identification of hydrocarbon filled layers in deepwater areas［J］.First Break，2002，20:144－152.

［5］ELLINGSRUD S，EIDESMO T，JOHANSEN S，et al.Remote sensing of hydrocarbon layers by seabed logging(SBL):results from a cruise offshore Angola［J］.The Leading Edge，2002，21(10):972－982.

［6］JOHANSEN S，AMUNDSEN H，RØSTEN T，et al.Subsurface hydrocarbons detected by electromagnetic sounding［J］.First Break，2005，23(1):31－36.

［7］AMUNDSEN L，LØSETH L，MITTET R，et al.Decomposition of electromagnetic fields into upgoing and downgoing components［J］.Geophysics，2006，71(5):G211－G212.

［8］ZIOLKOWSKI A，HALL G，WRIGHT D，et al.Shallow marine test of MTEM method［C］//76th Annual International Meeting，SEG，Expanded Abstracts，c2006:729－734.

［9］CONSTABLE S，WEISS C.Mapping thin resistors and hydrocarbons with marine EM methods:insights from 1D modeling［J］.Geophysics，2006，71(2):G43－G51.

［10］UM E，ALUMBAUGH D.On the physics of the marine controlled source electromagnetic method［J］.Geophysics，2007，72(2):WA13－WA26.

［11］WEISS C.The fallacy of the“shallow－water problem”in marine CSEM exploration［J］.Geophysics，2007，72(6):A93－A97.

［12］LØSETH L，PEDERSEN H M，BJØRN Ursin，et al.Low－frequency electromagnetic fields in applied geophysics:waves or diffusion［J］.Geophysics，2006，71(4):W29－W40.

［13］ANDREIS D，MACGREGOR L.Controlled－source electromagnetic sounding in shallow water:principles and applications［J］.Geophysics，2008，73(1):F21－F32.

［14］CHEN J，ALUMBAUGH D.Three methods for mitigating airwaves in shallow water marine CSEM data［C］//79th Annual International Meeting，SEG，Expanded Abstracts，c2009:785－789.

［15］LØSETH L，AMUNDSEN L.Removal of air－responses by weighting inline and broadside CSEM/SBL data［C］//77th Annual International Meeting，SEG，Expanded Abstracts，2007:529－533.

［16］MITTET R.Normalized amplitude ratios for frequencydomain CSEM in very shallow water［J］.First Break，2008，26:47－54.

［17］SASAKI Yutaka，MEJU M A.Useful characteristics of shallow and deep marine CSEM responses inferred from 3D finite－difference modeling［J］.Geophysics，2009，74(5):F67－F76.

［18］刘长胜，EVERETT M E，林君，等.海底电性源频率域CSEM勘探建模及水深影响分析［J］.地球物理学报，2010，53(8):1940－1952.LIU Chang－sheng，EVERETT M E，LIN Jun，et al.Modeling of sea floor exploration using electric－source frequency－domain CSEM and the analysis of water depth effect［J］.Chinese J Geophys(in Chinese)，2010，53(8):1940－1952.

［19］WARD S H，HOHMANN G W.Electromagnetic theory for geophysical applications:electromagnetic methods in applied geophysics，No.1［M］.Tulsa:Soc Explor Geophys，1988:131－311.

［20］LIEN M，MANNSETH T.Sensitivity study of marine CSEM data for reservoir production monitoring［J］.Geophysics，2008，73(4):F151－F163.

［21］CONSTABLE S C.Ten years of marine CSEM for hydrocarbon exploration［J］.Geophysics，2010，75(5):A67－A81.

［22］EDWARDS N.Marine controlled source electromagnetic:principles，methodologies，future commercial applications［J］.Surveys in Geophysics，2005，36(2):675－700.

(编辑 修荣荣)

Analysis of air wave interaction mechanism and effect of sea water depth on electromagnetic prospecting

SHEN Jin－song1，2，3，ZHAN Lin－sen1，WANG Peng－fei1，MA Chao1，LIAN Fu－ming1

(1.College of Geophysics and Information Engineering in China University of Petroleum，Beijing 102249，China;2.State Key Laboratory of Petroleum Resource and Prospecting in China University of Petroleum，Beijing 102249，China;3.CNPC Key Physical Exploration Laboratory in China University of Petroleum，Beijing 102249，China)

Based on the analysis of electromagnetic(EM)potential and electromagnetic field of 1D layer model，the interaction relationships of EM fields among air，sea water layer and undersea formation were established by using mode decomposition theory of EM field.Based on the presumed infinite sea water model and five－layer model，the EM field expressions of the TE and TM modes which were decomposed from the EM responses excited by the horizontal electric dipole(HED)source were derived.The variation laws of critical offsets with the under sea floor conductivity and sea water depth.It is pointed out that the conventional recognition of former researchers of the boundary depth of 300 m between the deep sea water and shallow water has drawbacks.Theoretical analysis shows that the air wave interaction with signals from other media is strongly coupled，and the ways that the horizontal and vertical electromagnetic components，also the TM mode and the TE mode are contaminated by the air waves are very different.Numerical results show that the air wave is a kind of diffusive wave interacted among sea surface，sea water and undersea formation，and the effects of the air wave interaction on TM and TE modes present significant differences.And the vertical componentEzhas only TM mode and is affected by the air wave on the least degree.Therefore，measurement ofEzcomponent is of helpful in reducing the effects of the air wave.In practical use，it is necessary to define the critical offset by considering the relationship among under sea floor formation conductivity，sea water depth and the offset，and the conventional boundary concept between deep water and shallow water has drawbacks.

electromagnetic prospecting;electromagnetic field;electromagnetic waves;electric conductivity;air wave interaction;mode decomposition;layer medium model

P 631.4

A

10.3969/j.issn.1673－5005.2011.06.008

2011－02－20

国家“973”重点基础研究发展计划项目(2007CB209607);中国石油天然气集团公司基础研究项目(07A10303)

沈金松(1964－)，男(汉族)，江苏吴江人，研究员，博士，主要从事电磁探测与地球物理测井方法理论及应用研究。

1673－5005(2011)06－0051－08