基于统计学检验指标的燃气轮机部件特性方程拟合次数的选择

赵雄飞，刘永葆，贺 星，刘建华

（海军工程大学 船舶与动力学院，武汉 430033）

0 引言

在燃气轮机气路故障诊断过程中，针对所给出的燃气轮机各部件特性曲线以及实际工作曲线，建立其部件特性方程，确定研究对象的精确数学模型，是实施正确诊断的必要前提。在一般情况下，采用曲线拟合的方法来建立部件特性方程。周密[1]在研究燃气轮机气路故障诊断中，采用最小二乘法对压气机与涡轮部件特性曲线进行拟合，取得了较好的拟合结果；Taik-Min Lee等[2]将精确的双弧线拟合算法应用到非球面加工，拟合结果与球面实际情况吻合，为进一步分析奠定了基础；贺星[3]针对燃气轮机性能退化，在建模过程中采用了改进的麦夸尔特算法拟合部件特性曲线；袁萃等[4]在飞行器飞行仿真研究中，应用曲线拟合方法替代插值方法，减少了输入参数数量，从而提高了仿真精度；方前[5]对风扇特性曲线进行拟合，考虑了边界约束条件，提高了拟合精度；Verboven.P等[6]对多幅值相应曲线进行拟合，并将拟合结果用于模型的参数估计中，取得了较好的效果；曾嵘[7]将SVM算法中的回归机应用于曲线拟合过程中，从而对机械故障进行诊断，但在实际拟合过程中，如何选择合适的拟合函数与拟合次数，对其精确度有着至关重要的影响；刘喜超等[8]采用偏最小二乘法对压气机特性曲线进行了拟合，并用相对误差和相关系数平方指标评价了拟合结果；Bo-Suk Yang[9]采用均方差、标准差线性关系度来评定拟合精度，均取得了较好的效果。赵世荣[10]提出了以训练样本、测试样本误差平方和的平方根作为建模的评价标准来评定所建模型的准确性。

本文以5种拟合检验指标，结合所选算法优选出最佳的特性方程拟合次数，使得到的拟合方程在最大程度上反映实际曲线运行规律，从而降低了建模误差。

1 统计学检验指标的引入

本文引入5个统计学拟合检验指标，以检验特性方程拟合次数是否恰当，并计算得出最佳的拟合次数。

1.1 相关系数平方指标R2

式中：yi为测量值为拟合值为样本均值。

相关系数平方越接近1，拟合效果越好。

1.2 均方差指标RMSE

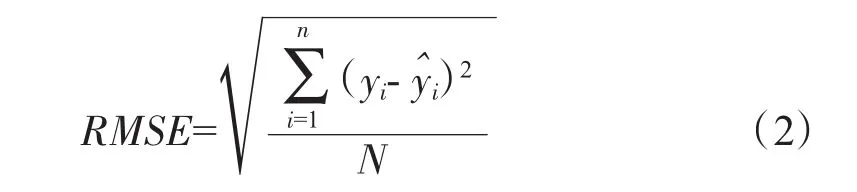
式中：N为实际测量样本总数。

均方差越接近0，拟合效果越好。

1.3 相对误差平方和SRES

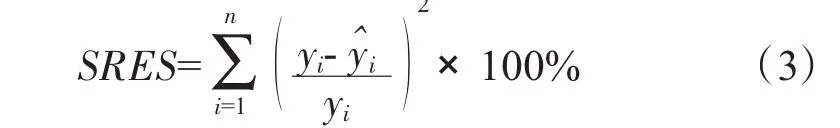
相对误差平方和越小，拟合效果越好。

1.4 检验指标Q1

在式（4）中，假设yi服从正态分布，卡方系数χ2以自由度（N-n-1）为期望值。当 χ2-（N-n-1）越小，则拟合精度越高；在（N-n-1）附近时，拟合是合理的。反之，当＞＞（N-n-1），则可能是由选择的拟合函数形式不合适、方差估计太小、样本误差等原因造成。其中n+1是多项式系数的数目。由于本文数据是通过部件特性曲线离散化后得到的结果，所以忽略后2种因素，检验指标Q1主要检验拟合函数是否符合样本本身的内在规律。

1.5 检验指标Q2

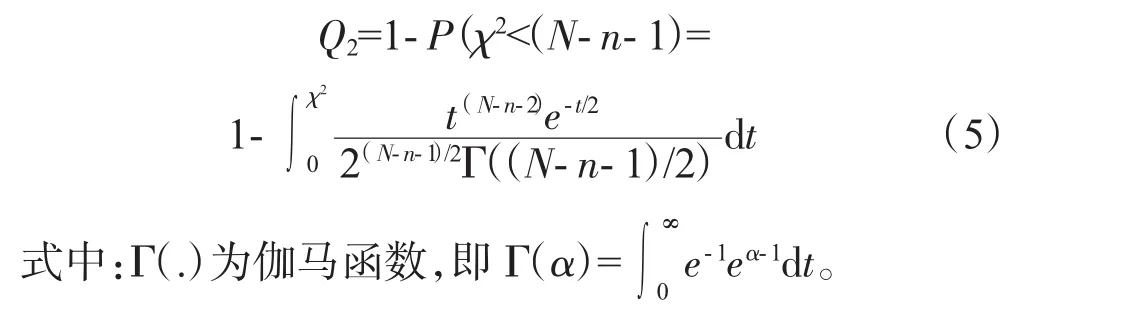
该检验指标Q2与0.5接近，则表示多项式拟合次数适当。

2 拟合模型的选择

对于一般的特性曲线，通常采用多项式模型对数据进行描述，对于拟合目标形如 y（x）=f（a,x）=a1xn+a2xn-1+L+anx+an+1的n阶多项式模型，通常要求取参数 a1、a2、L、an、an+1使下面的相对误差 ψ2量最小。

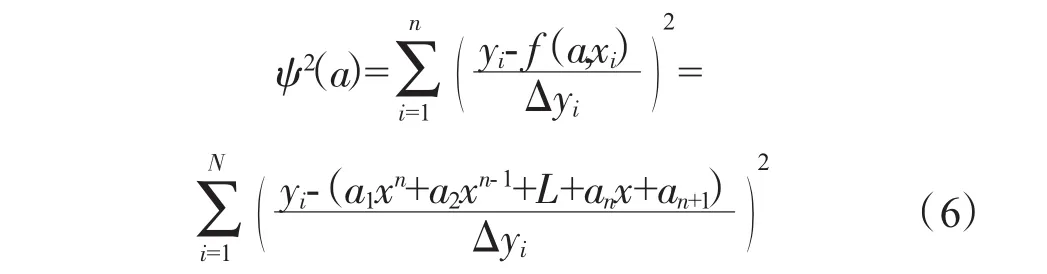
在Δyi=Δy不变的假设下得到式（6）的最小解为

通过对特性曲线进行多项式拟合得到特性方程。其实质是多元回归问题，一般采用结合法[8]或2步法[11]，本文采用2步法对部件特性曲线进行拟合。

3 算例分析

3.1 拟合次数的选择

以某型3轴燃气轮机的高压压气机为例，其结构如图1所示[12]，压气机通用特性曲线如图2所示。从图2中可见，高压压气机折合流量与高压压气机压比和折合转速存在一定的函数关系。将压气机压比与折合转速作为自变量，而将折合流量作为因变量，4个参数之间存在如下关系

用多项式进行曲线拟合，当最高次数n≥7时，经过大量计算及理论分析均表明其方程的系数矩阵是严重病态的。所以考虑最高次数n≤6时对高压压气机的1.0工况等转速线上的“折合流量-压比”关系曲线进行研究，并按照拟合检验指标寻找并确定“折合流量-压比”之间的最佳函数关系，其结果见表1。

表1 不同最高拟合次数检验指标值

从表1中可见，随着拟合次数n的增加，R2、RMSE、SRES呈越来越好的趋势。由此表明，在特性曲线多项式拟合中，随着拟合次数的增加，精度提高。但是，从Q1、Q2可知，在n≥4时的拟合过程中出现过拟合，拟合曲线纳入了噪声，所以，在保证拟合精度的前提下有避免纳入噪声的原则，这里选择n=3作为该曲线的最佳拟合次数。

3.2 拟合误差分析

选择n=3作为部件特性方程的拟合次数，可以得到该测量值与拟合值的相对误差，如图3所示。

从图3中可见，当选择n=3时，对应的各工况下的最大误差为0.2%，其结果满足拟合精度。根据上述分析，绘出在拟合曲线中原数据点与拟合点的对比曲线，并给出其残差分布情况，其结果如图4所示。

从图4中可见，通过正确地选择拟合次数，其所得到的拟合曲线残差为±5×10-13，拟合效果较好。

3.3 拟合结果

上述分析可知压气机折合流量是关于压比与折合转速的函数，所以首先通过1次拟合分别得到各工

况下关于“折合流量-压比”之间的函数关系

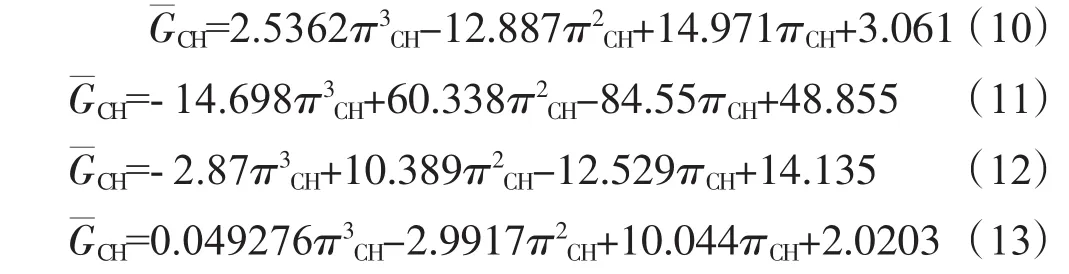
然后对式中的各项系数进行2次拟合，得到关于“压比-折合转速”之间的函数关系

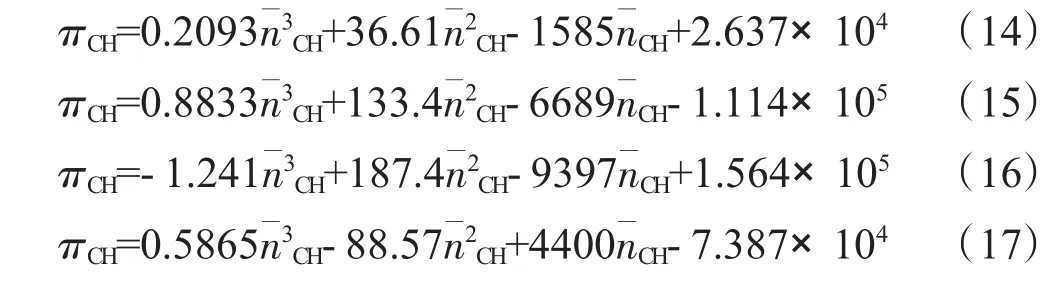
经过上述2步拟合之后，最终可以得到“折合流量-压比-折合转速”之间的函数关系式

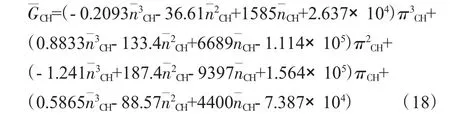
4 结论

本文将5个统计学拟合检验指标引入燃气轮机部件特性方程的拟合过程中，通过实际算例分析得出了最佳的拟合次数。分析表明：所选择的拟合次数能够较好的对曲线的实际情况进行描述。得到拟合值与测量值的相对误差为±0.2%，残差范围为±5×10-13，进一步证明了拟合误差小，与曲线吻合度高。综合应用上述检验指标所获得的特性方程的最佳拟合次数具有可行性与可靠性。引入检验指标避免了在拟合过程中经验化选择拟合次数的问题，为特性曲线拟合次数从定性选择过渡到定量计算提供了1条可行之路。

[1]周密.基于信息融合技术的燃气轮机气路故障诊断研究[D].武汉：海军工程大学，2009.

[2]Lee T M，Lee E K，Yang M Y.Precise bi-arc curve fitting algorithm for machining an aspheric surface[J].International Journal of Advanced Manufacturing Technology，2007，31（11-12）：1191-1197.

[3]贺星.基于热力学功势的燃气轮机性能退化研究[D].武汉：海军工程大学,2010.

[4]袁萃，杨青真，陈立海.飞行器特性曲线拟合与飞行仿真研究[J].计算机仿真，2008，25（2）：53-57.

[5]方前.航空发动机系统建模与故障诊断研究[D].西安：西北工业大学，2005.

[6]Verboven P，Guillaume P，Cauberghe B. Multivariable frequency-response curve fitting with application to modal parameter estimation[J].Automatic，2005，41 （10）：1773-1782.

[7]曾嵘.支持向量机在设备故障诊断中的应用研究 [D].长沙：中南大学，2007.

[8]刘喜超，唐胜利.基于偏最小二乘法的压气机特性曲线的拟合[J].汽轮机技术，2006，48（5）：327-329.

[9]Suk B Y，Widodo A.Support vector machine for machine fault diagnosis and prognosis[J].Journal of System Design and Dynamics.2008，2（1）：12-23.

[10]赵世荣.航空发动机自适应建模及故障诊断[D].南京：南京航空航天大学，2007.

[11]翁史烈.燃气轮机性能分析 [M].上海：上海交通大学出版社，1987.

[12]刘永葆.舰用燃气轮机 [M].武汉：海军工程大学出版社，2007.