轮盘弹塑性盘破裂准则的建立及变厚度轮盘破裂转速预测

万江艳，周柏卓

（中航工业沈阳发动机设计研究所，沈阳 110015）

轮盘弹塑性盘破裂准则的建立及变厚度轮盘破裂转速预测

万江艳，周柏卓

（中航工业沈阳发动机设计研究所，沈阳 110015）

建立了与材料延伸率相关的轮盘弹塑性破裂准则。为了验证所提出破裂准则的正确性，采用非线性有限元对变厚度轮盘破裂试验件的破裂转速进行了预测，并与试验结果进行了对比。结果表明，二者吻合很好。

轮盘；破裂准则；破裂转速；材料非线性；非线性有限元法

0 引言

航空发动机推重比的提高，对发动机关键构件的强度设计提出了更高要求。在满足强度储备标准的前提下，要求尽量减轻各部件的质量。轮盘是发动机最关键的部件之一，美国对民用燃气涡轮发动机的统计表明，所有轮盘和绝大多数轮缘的破裂均属于非包容性故障,可导致灾难性后果。由于轮盘的破裂碎片打穿发动机机匣后，便可能切断油路或操纵系统，穿过油箱或座舱，造成飞机损坏、人员伤亡的严重后果。因此，精确预测轮盘的破裂转速十分重要。

目前，在工程上通常采用平均应力方法来计算轮盘破裂转速，即用轮盘平均周向、径向应力达到材料的拉伸强度时轮盘的转速作为计算的破裂转速。该方法简便，且对于均温理想塑性材料的对称等厚盘的计算精度很高，但对于硬化材料和非对称盘误差较大，对于复杂的结构或带轴颈结构，其计算结果不精确且很大程度依赖于设计者的经验。

本文提出了与材料延伸率相关的轮盘破裂准则，并对北京航空航天大学设计的变厚度轮盘破裂试验件[1-3]的破裂转速进行了预测。

1 轮盘破裂准则

在单调增加的载荷作用下，当结构内任一局部点的应力应变状态达到光滑拉伸试件破坏时的状态时，该点被破坏。光滑试件的应力状态为单向应力状态，而真实构件断裂关键部位往往处在复杂应力状态中。对于韧性较好的材料可以将破裂准则推广为：在单调增加的载荷作用下，当结构内任一局部点的Von-Mises当量应力应变达到光滑试件破坏时的应力应变时，该点被破坏。

材料的延伸率表示光滑试件在单调增加的载荷作用下所能承受的最大平均塑性应变，即延伸率定义为试件拉断后测量段（标距）的塑性变形量除以测量段的原始长度。因此，材料的延伸率可以描述材料破坏前承受塑性变形的能力，轮盘的破裂准则可进一步扩展为：在单调增加的转速作用下，当轮盘内任一局部点的当量塑性应变达到材料的延伸率时，这时的转速就是轮盘的破裂转速。

当采用大应变有限元计算方法时，需要用对数应变。当量塑性应变达到材料的延伸率时，对应的对数塑性应变为

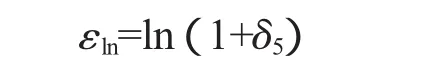
因此，当采用大应变有限元计算方法时，轮盘的破裂准则可以描述为：在单调增加的转速作用下，当轮盘内任一局部点的当量塑性应变εln达到ln（1+δ5）时，该点被破坏。在转速单调上升过程中，只要结构的任一局部点出现裂纹，则裂纹将迅速扩展，结构将不再具有承受继续增加载荷的能力，这时的转速就是轮盘的破裂转速。

2 试验轮盘破裂转速预测

为了验证所提出破裂准则的正确性，对北京航空航天大学设计的变厚度轮盘破裂试验件的破裂转速进行预测，并与试验结果进行对比。

2.1 试验件的基本参数

轮盘材料为韧性和塑性较好的A3钢，其材料数据见表1。轮盘中心孔、轮缘、叶尖的直径分别为100、150、300mm，如图 1所示。取轮盘破裂时的局部塑性应变为10%。

表1 A3钢材料力学性能数据

2.2 2维轴对称模型

取从盘心到盘缘的部分为研究对象，用8节点轴对称单元进行描述，共划分为3036个单元，9469个节点。在轴颈端面1点施加轴向位移为0的边界条件，在盘体上施加轮盘本身质量所产生的离心力，在盘缘处以面力的形式施加模拟叶片的离心载荷，其2维轴对称有限元模型如图2所示。

叶片所产生的离心力为

F=Mω2R （1）

式中：F为叶片离心力；M为叶片质量，M=3.5873kg；ω 为轮盘的旋转角速度，rad/s；R 为叶片质心半径，R=126.98mm。

轮盘破裂前的当量应力和塑性应变分布分别如图3、4所示。轮缘（A点）、盘心孔边（B点）及轴颈（C、D点）处的当量塑性应变随转速变化的关系如图5所示。

从图5中可见，当转速小于9000r/min（0.75×12000r/min）时，轮盘几乎没有塑性应变；随着转速的增大，各点的塑性应变缓慢增加，大小依次为B、C、D、A点，D点的塑性应变随着转速的增大，前期增加较慢，后期增加较快；当转速达到12192r/min时，D点的塑性应变已经超过B点的；当转速达到12258r/min时，D点的塑性应变达到10%，此时的转速为2维轴对称模型预测的轮盘破裂转速。

2.3 3维实体模型

由于具有对称性，取整个结构的1/40为研究对象，用20节点3维实体单元进行描述，共划分为3108个单元，15440个节点。在轴颈端面施加轴向位移为0的边界条件，在对称面上施加周向位移为0的边界条件，施加轮盘及叶片质量所产生的离心力。3维有限元模型如图6所示。

轮盘破裂前的当量应力和当量塑性应变分布分别如图 7、8所示，A、B、C、D 点处的当量塑性应变随转速变化关系如图9所示。

从图8中可见，当量塑性应变在轮缘处最大，在盘心处次之。从图9中可见，当转速小于8500r/min（0.71×12000r/min）时，轮盘几乎没有塑性应变；随着转速的增大，A点的当量塑性应变增加较快，B、C、D点的当量塑性应变增加比较缓慢；当转速达到11880r/min时，A点的当量塑性应变已经达到10%，此时的转速为3维有限元模型预测的轮盘破裂转速。

2.4 结果分析

3维模型能够描述叶片与轮盘转接处圆角的应力集中情况，最大当量塑性应变就发生在此处，当此处的当量塑性应变达到破裂条件时，轮盘破裂。由于2维轴对称模型不能描述叶片与轮盘转接处圆角的应力集中情况，最大当量塑性应变在盘心处。2维轴对称模型和3维有限元模型预测的破裂转速与试验结果的对比见表2。

表2 破裂转速预测结果与试验结果对比

3 结论

（1）用弹塑性、大应变、大变形的非线性有限元方法对轮盘破裂转速进行预测时，其局部塑性应变不再是小量，应该对应力应变曲线进行修正，用真实的应力应变曲线。

（2）本文所提出的与材料延伸率相联系的轮盘的破裂准则可以较精确地描述轮盘的破裂行为。用弹塑性、大应变、大变形的非线性有限元方法可以较精确地描述轮盘破裂前的变形行为，并能清晰表示出轮盘破裂的最薄弱部位。

（3）2维轴对称有限元模型简单、计算速度快，可以较准确地预测轮盘沿子午面和圆柱面的破裂行为。但由于在2维轴对称模型中对叶片和轮缘凸块的作用只能作为用在轮缘上的等效面力来模拟，所以不能描述榫齿连接部位的破裂行为，此时必须用3维有限元模型，盘榫连接部位采用接触边界条件来描述。

[1]洪其麟，王屏.计算轮盘破裂转速大变形解析法[J].航空动力学报，1990，5（4）：321-324.

[2]郑祺选.轮盘破裂转速试验研究 [J].航空动力学报，1990，5（4）：318-320.

[3]古爱军，张学仁.轴流式轮盘破裂转速的数值计算方法[J].航空动力学报，2001，16（3）：287-290.

[4]航空发动机设计用材料数据手册编委会.航空发动机设计用材料数据手册：第3册[M].北京：航空工业出版社，2008.

[5]机械工程材料性能数据手册编委会.机械工程材料性能数据手册[M].北京：机械工业出版社，1995.

Elastic-plastic Disc Burst Criteria Establishment and Variable Thickness Disk Burst Rotational Speed Prediction

WAN Jiang-yan ZHOU Bai-zhuo
（AVIC Shenyang Aeroengine Research Institute,Shenyang 110015,China）

The elastic-plastic disc burst criteria related to material elongation was established.In order to validate the criteria,the burst rotational speed of the variable thickness test disc were predicted using the nonlinear finite element method.The prediction were compred with the test data.The results show the prediction were in accord with the test data.

disc;burst criterial;burst rotational speed;nonlinear material;nonlinear finite element method

万江艳（1973），女，工程师，从事航空发动机强度设计工作。