稳态温度场作用下涡轮叶片振动特性的研究

艾书民，王克明，缪 辉，赵 帅

(沈阳航空航天大学动力与能源工程学院，沈阳 110136)

发动机实际工作过程中，叶片由于受温度载荷等方面因素影响，其振动问题较常温状态下更为复杂，开展温度场作用下叶片振动问题的研究尤为重要，也更具有工程价值。目前国内外关于结构耦合温度场情况下振动特性问题分析还不是非常成熟。肖俊峰等人建立了叶片温度场和热应力场的三维有限元分析模型和方法［1］，但对于温度场近似问题尚未展开研究，朱向哲等人分析了稳态温度场对转子系统的影响［2］，而对于温度场施加方法未展开讨论，Librescu L等人对高温环境下薄壁件的振动特性和稳定性开展了一些研究工作［3］，对于航空发动机部件在温度场下的振动特性研究也有一定的参考价值。本文对某型发动机涡轮叶片在温度场作用下的温度载荷施加方案进行了研究，得到了一种稳态一维温度场的简化方案，并利用有限元软件检验了该方案的可行性。

1 基本理论方法

1.1 稳态一维温度场的近似插值方法

物质系统内各个点上温度的集合称为温度场。它是时间和空间坐标的函数。不随时间而变的温度场称为稳态温度场，即T=f(x，y，z)，此时为三维稳态导热。对于一维温度场，稳态热分析时可将温度函数表示为T=f(x)，即稳态一维温度场都可以表示为几何参数的函数，对于工程实际中一维温度分布函数往往比较复杂，对温度载荷的处理比较困难，如果能够对一维温度函数进行分析并根据其特点在函数图线上选出一组较有代表性的关键点数据，理论上可以结合一维温度场分布特点采用选取的关键点数据对其进行一维近似插值，从而简化结构温度场分布，为进一步的有限元分析提供可行的温度载荷施加方案。

图1 一维线性分段插值

如图1所示，设一维温度场函数表达式为T=f(x)，在x方向上取i个点对函数进行线性分段插值，最终实现由分段函数来代替一维温度场分布函数。

1.2 稳态温度场作用下结构振动特性的有限元分析

温度场与结构的耦合分析包括完全耦合和场序热结构耦合，考虑到本文涉及的叶片模型在结构变形对温度场的作用非常微弱，故采用场序热结构耦合方案研究［5］。场序热结构耦合理论的主要思想是先利用初始温度对结构进行稳态温度场分析，得到结构在稳态温度场下的节点温度文件，然后转换分析单元，修改结构材料特性曲线，将热分析中的得到的节点温度文件导入并作为温度载荷施加到结构节点上去，最后进行分析计算，求解并得到结构振动特性数据。

一维稳态温度场直接施加于结构难度较大，可以采用线性分段插值拟合方法先对温度场进行适当简化。目前有限元软件都具备一定的插值运算能力，在温度场耦合结构振动问题方面，比较优秀的有限元分析软件有ANSYS软件，该软件提供了近似的插值拟合运算方案，具有强大的热－结构耦合分析能力，能够胜任稳态温度场作用下的结构振动分析问题。

2 算例

2.1 涡轮叶片建模与网格划分

涡轮叶片模型参考某型发动机第一级涡轮转子叶片，实际的叶片结构比较复杂，对于叶片振动问题可对叶片中冷却孔和榫头进行一定的简化。

实体模型保留了叶片的叶身叶冠等大部分关键特征，对榫头和冷却导管进行了简化，榫头部分为划分六面体网格忽略榫齿结构，由于在叶片的振动问题分析中，边界条件一般的处理方法是将榫头两侧齿面所有节点施加全约束［4］，对榫头两侧进行适当简化对于计算振动问题是可行的，考虑振动问题时冷却导管对计算结果影响较小可以忽略。

图2 涡轮叶片的实体模型和有限元模型

本文采用ANSA网格划分软件对叶片模型进行手动网格划分，得到了叶片的六面体单元网格有限元计算模型，在对计算结果进行分析时，采用四面体单元网格划分模型作为对比参照。

2.2 涡轮转子叶片的温度沿径向分布特点

图3表示了实际发动机中燃气温度与叶片工作温度沿叶高的分布规律。可以看出涡轮转子叶片两端温度较低，它的最大值约在叶片中部，在叶根处由于应力最大，叶尖处叶型较薄，为提高疲劳强度和叶片的寿命，根据涡轮工作叶片的要求，希望叶根和叶尖处温度低些［6］。

图3 叶片叶身径向温度分布图线

榫头区域温度分布如图4所示，虽然榫头处温度分布较为复杂，但仍近似满足线性规律。

图4 叶片榫头区域温度分布状态

2.3 一维温度场的拟合简化

利用第1节中提出的一维温度场插值方法对叶片沿径向一维温度场进行分段插值拟合，将榫头与叶身分开进行插值计算，叶身与榫头部分采用直接过渡的插值方法处理。

图5 叶身径向温度分布的分段拟合

图6 榫头区域沿径向温度分布的分段拟合

根据图5和图6中的插值方式得到涡轮叶片叶身和榫头区域插值关键点，整理为表1和表2。

表1 叶片叶身一维温度场插值节点数据(坐标原点O2)

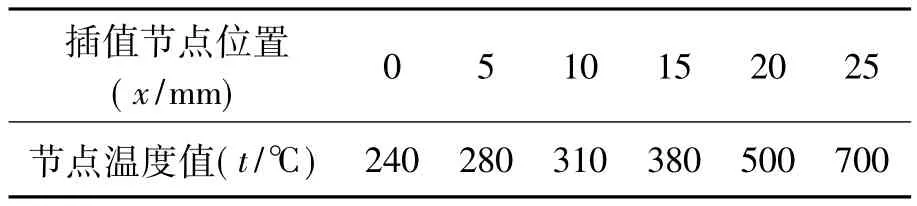
表2 叶片榫头区域一维温度场插值节点数据(坐标原点O1)

2.4 计算与求解

先对叶片进行热分析，由以上分析中得到的温度插值数据作为初始参数施加到结构上。在材料属性的处理上，一般方法是通过输入离散的点值来表示可变材料属性的，如图7所示［7］。求解并得到叶片的一维稳态温度场，如图8所示。

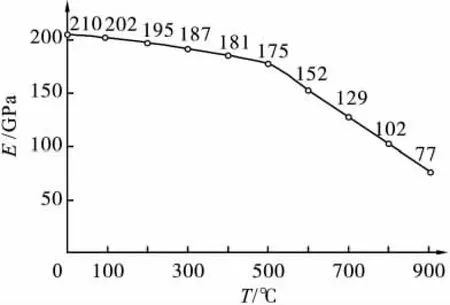
图7 材料特性离散点插值曲线图

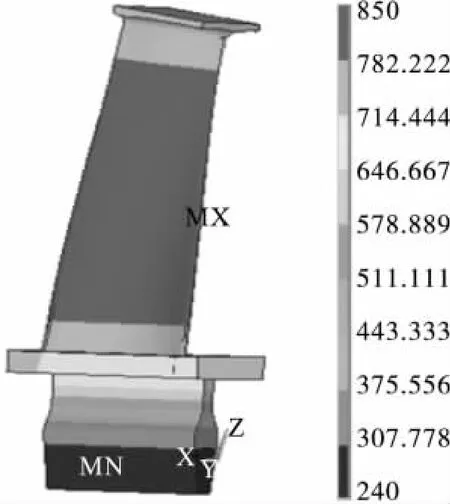
图8 热分析得到的叶片稳态一维温度场

将分析类型由热分析更改为热－结构耦合分析并转换分析单元，对叶片进行热—结构耦合分析，材料特性参数如图7所示，以离散点形式输入，榫头的榫齿区域表面节点施加位移全约束，将热分析得到的节点温度文件数据导入并作为结构的温度载荷。

计算得到叶片在温度场作用下的前十阶固有频率和模态，与常温状态下计算结果进行比对，整理得到表三。(数据取前十阶，单位为Hz)模态图取第1、3、5、7 阶作为参考对比。

常温下涡轮叶片模态(1、3、5、7 阶):

图9 常温状态下叶片振动模态

温度场下涡轮叶片模态:(1、3、5、7 阶)

图10 涡轮叶片在温度场作用下模态

对于涡轮叶片振动问题而言，动频是需要考虑的重要因素，本文对在不同转速、不同状态下的叶片动频进行了对比计算，计算结果整理在表四中，通过对比可以发现计算得到的动频值在所考虑的转速范围内大多小于静频值，似乎与动频值始终大于静频值的基本常识相悖，实际上这是考虑了温度场作用的影响而引入的修正［8－9］。

表3 不同状态下的叶片固有频率计算值对比

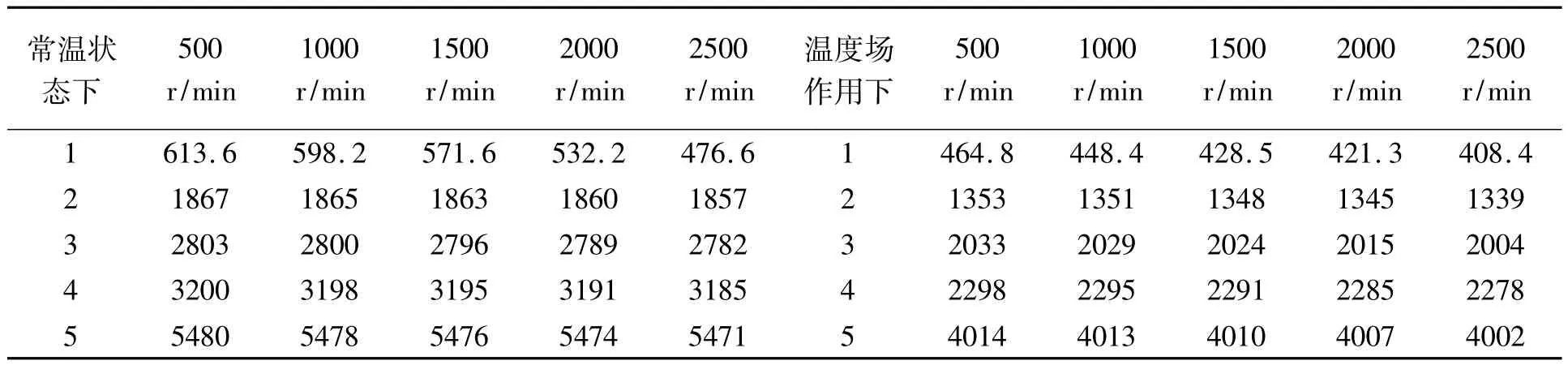
表4 常温状态与温度场作用下叶片动频计算值对比

3 计算结果分析验证

3.1 采用不同单元及不同网格划分方法的分析计算验证

采用不同单元类型对叶片振动特性进行分析计算，对比计算分析结果见表五。(数据取前十阶，单位为Hz)

三种不同单元中solid185、solid186单元在计算精度方面要优于solid45单元，而节省计算时间方面采用solid185单元要好于solid186单元，综合对比可见采用solid185单元下的计算结果在三种单元计算结果对比中是最为理想的。在不同网格划分状况下的对比即统一采用该单元类型。

采用四面体自由网格划分方式重新划分叶片模型，重新计算并对计算结果进行对比。(数据取前十阶，单位为Hz)对比结果见表6。

表5 采用不同单元类型下的叶片固有频率计算值

表6 不同网格划分方式情况下的计算结果对比

3.2 误差分析

根据表1和表2提供的插值点对叶身和榫头的一维温度场进行三次样条函数拟合得到涡轮叶片榫头区域与叶身区域一维温度场分布的三次拟合函数表达式为:

分别对两个函数求定积分，并计算分段插值函数所围成多段梯形区域的面积，比较并列如表7所示:

表7 插值误差分析

4 结论

(1)通过对一维稳态温度场作用下叶片的振动特性计算以及对分段插值方法的误差分析，说明采用分段插值方法在处理一维稳态温度场简化和温度载荷施加问题方面是可行而且可靠的。

(2)考虑温度场作用下的涡轮叶片固有频率计算值要低于常规方法不考虑温度场情况下的计算值，通过本文的研究进一步说明温度对叶片振动特性的影响是显著的。

(3)温度场作用下叶片动频计算值与采用常规经验公式下计算结果相比较偏小，说明温度场作用对叶片动频的影响是除转动惯量之外的一个重要的因素，在涡轮转子叶片动频计算时不应当被忽略。

［1］肖俊峰，朱宝田，丰镇平，等.具有温度场的冷却叶片振动特性计算方法研究［J］.燃气轮机技术，2006(3):28－31.

［2］朱向哲，贺威，袁惠群.稳态温度场对转子系统振动特性的影响［J］.东北大学学报(自然科学版)，2008(1):114－116.

［3］Librescu L，Oh S－Y，Song O.Thin－walled beams made of functionally graded materials and operating in a high temperature environment:vibration and stability.Thermal Stresses［J］.2005(2):649 －712.

［4］王相平，徐鹤山.有限元计算中的叶片边界条件的选取［J］.航空发动机，1998(4):43－46.

［5］陈火红，祁鹏.MSC.Patran/Marc培训教程和实例［M］.北京:科学出版社，2004:330－332.

［6］邓明，刘长福.航空发动机结构分析［M］.西安:西北工业大学出版社，2006:131.

［7］潘留仙，焦善庆，杜小勇.高温下常用合金材料线胀系数、杨氏模量与温度的关系［J］.湖南师范大学自然科学学报，2000(2):47－51.

［8］杨文庆，孙强，马龙，等.某型航空发动机压气机叶片振动静频与动频的关系［J］.空军工程大学学报(自然科学版)，2005(5):5－7.

［9］孙强，张忠平，柴桥，等.航空发动机压气机叶片振动频率与温度的关系［J］.应用力学学报，2004(4):137－139.

［10］李川，王克明，尹帮辉，等.某型航空发动机低压涡轮盘的强度计算［J］.沈阳航空工业学院学报，2009，26(4):1 －4+8.

［11］吴志广，王克明，张利民.静子叶片内环结构对机匣动力特性的影响［J］.沈阳航空工业学院学报，2010，27(4):23 －26.