Liesegang图案实验的开发和教学实践*

郑菊花 潘长伟 蒋荣立 何亚群 高庆宇

(中国矿业大学化工学院 江苏徐州 221116)

沉淀溶解平衡是无机与分析化学课程中的四大平衡理论之一。通常沉淀反应在水溶液中进行，得到晶形、凝乳状或无定形沉淀。为配合学生对这部分实验内容的学习，我们除了安排了Al2O3，BaSO4等制备生成实验，还对应用化学专业的学生开设了Liesegang图案实验；该实验以凝胶为介质，可以得到丰富多彩的沉淀图案。Liesegang图案实验最早是在1896年由德国科学家Raphael E.Liesegang[1]发现的。当时他在一块玻璃板上涂上明胶层，胶体中含有重铬酸钾稀溶液，之后将硝酸银晶体置于明胶表面上，一段时间后出现了由重铬酸银形成的环绕晶体的同心环，这一周期性沉淀图案被称为Liesegang图案。此后的大量研究发现，Liesegang图案不仅有环状图案，还有螺旋状图案[2]，树枝状图案[3]，移动的沉淀图案[4]等，其现象本身蕴含着丰富的动力学行为。

Liesegang图案在自然界中广泛存在，如玛瑙石上的纹理结构、孔雀石(碱式碳酸铜) 上的清晰环线图案、病人囊腺中的环状结石等，与凝胶中时空有序沉淀的形成具有相同的本质根源，均属于过饱和溶液沉淀与扩散耦合产生的时空自组织现象。由于Liesegang图案实验现象丰富，近10年来不断有新的研究成果报道，所以更能激发学生的学习兴趣，扩大学生视野，有助于学生加深理解沉淀溶解平衡理论。

1 实验目的

(1) 了解Liesegang图案发展历史，掌握Liesegang图案基本理论和实验操作。

(2) 加深对沉淀溶解平衡及沉淀理论的理解。

(3) 培养学生的科技文献阅读能力，学习查阅文献并设计实验方案。

(4) 掌握相关仪器的使用和实验数据的分析方法，通过数值计算模拟Liesegang图案。

2 Liesegang图案的基本规律和形成机理

2.1 Liesegang图案的基本规律

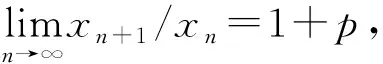
2.2 Liesegang图案的形成机理

100多年来，科学家试图用各种理论来解释Liesegang图案的形成，包括过饱和理论、继成核理论、Bradford吸附理论、絮凝理论、扩散波理论等，但至今还没有一种理论能解释所有的Liesegang现象。在这里我们介绍最具代表性的过饱和理论和继成核理论。

(1)过饱和理论。Ostwald[5]在1897年提出过饱和理论(the supersaturation theory)。该理论认为沉淀出现前，必须有某种程度的过饱和。当外电解质扩散到胶体中，与均匀分散在其中的内电解质发生反应，只有反应物的浓度积大于某一过饱和阈值时才能生成沉淀，而沉淀的形成消耗其周围的电解质，使反应物的浓度积降到过饱和阈值以下，沉淀不再生成，只有穿过这一区域后，反应物的浓度积达到过饱和阈值之上，沉淀才能再次形成。这一过程的重复导致周期性Liesegang图案的形成。

(2)继成核理论。1974年，Flicker和Ross[6]提出了继成核理论(the postnucleation theory)。该理论认为宏观可见的沉淀图案最初是由沉淀固体粒子在空间均相成核而得到的，而固体粒子的产生则是由于尺寸大小不同的粒子的稳定性不同造成的，这种现象的驱动力就是系统自由能最小(Ostwald熟化)。这一体系中，成核的粒子有大有小，大粒子尺寸的增加，会造成反应物的局部消耗，然后扩散传输就会向粒子尺寸增加的扰动区输送一个净质量流，从而导致附近自由能高的小粒子开始溶解，这样就造成了局部浓度的增加。因此Liesegang图案的形成是由于粒子尺寸的振荡而产生的。

3 实验体系、试剂和仪器

实验采用K2Cr2O7-AgNO3沉淀反应体系，在中性或弱碱性介质中，其总反应为：

试剂：明胶(生物试剂)，重铬酸钾(分析纯)，硝酸根(分析纯)，蒸馏水。

仪器：烧杯，培养皿，电热套，电子天平，恒温箱，CCD视频采集系统(WV/EP460，Japan)，PC计算机。

4 实验步骤

(1)明胶及K2Cr2O7溶液的制取。称取约5g明胶，转移至100mL烧杯中，加入50mL蒸馏水，静置约30min至明胶充分溶胀;将烧杯放在加热套上加热，调节温度在70～80℃之间，加热过程中用玻璃棒缓慢搅拌均匀至溶液变为澄清;再向明胶溶液中加入0.05g K2Cr2O7，继续搅拌10min至完全溶解;停止加热，冷却至室温。

图1 Liesegang图案的形成过程(a) 4h；(b) 11h；(c) 31h；(d) 50h

(2)明胶介质(K2Cr2O7溶液)的铸型。用注射器将烧杯中未凝结的明胶溶液转移到已经放置好棱柱的培养皿中，使明胶溶液在培养皿中的液面高度约为0.5cm;然后将培养皿置于恒温培养箱中的反应平台上，使胶体及K2Cr2O7溶液凝结成凝胶，放置过夜;第2天将培养皿中心的棱柱取出。

(3)Liesegang沉淀图案的形成。将棱柱取出后，明胶层中心会留下棱柱型的凹槽;向凹槽中加入预先配置好的1.0mol/L硝酸银溶液，硝酸银溶液开始扩散到凝胶中并与凝胶中的重铬酸银溶液反应。利用CCD视频采集系统(WVEP460，Japan)每隔30min采集一次图像。最后对形成的Liesegang图案进行数值模拟。

5 典型实验结果与数值模拟

5.1 实验结果

图1是外电解质为正方形边界条件下所形成的周期性沉淀图案，分别为反应进行4h、11h、31h、50h时用CCD摄像系统(WVEP460，Japan)拍摄得到的图片。随着外电解质向胶体中扩散，沉淀带的数量逐渐增加，但位于正方形边方向的沉淀带相对于角方向的沉淀带更早形成(见图1(c))，同时正方形角方向的沉淀带间距大于边方向的带间距，沉淀带出现了错位(见图1(d))，主要是因为边与角方向的沉淀带分别遵循不同的时间与空间定律。

5.2 数值模拟

5.2.1 模型

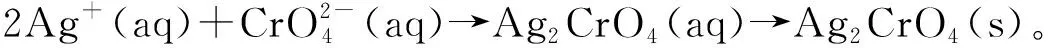
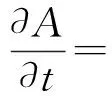
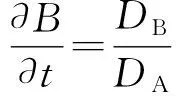
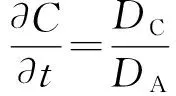
其中K是溶度积常数；C*是成核阈值；2是拉普拉斯算符；DA，DB，DC分别为物质A，B，C的扩散系数。θ(A2B-K)是步函数，其物理意义为：当A2B-K≥0时，θ=1；其他情况θ=0。R(A,B)可以用下式来描述：

R(A,B)=δ(cr+(1-cr)r)exp(-S2)

其中δ指中间产物C的增量，由(A-2δ)2×(B-δ)=K计算得到；r是一个随机数，取值区间[0，1]；S=A-B/A+B；cr是决定反应随机程度的参数，取值区间[0，1]，当cr=1，表示反应完全确定，当cr=0，反应完全由随机性决定；另外，反应过程的描述还需引入一个函数N(C，D)，如果当前位置有沉淀，则N(C，D)=1；如果当前位置没有沉淀，但周围格点有沉淀，且满足C>D*时，有沉淀产生，N(C，D)=1；另外,不管周围及当前有没有沉淀，只要满足C>C*，N(C，D)=1；其他情况下，N(C，D)=0。

模拟使用初始条件为A(x,t=0)=C(x,t=0)=D(x,t=0)=0，物质B均匀分配在整个反应区域，物质A置于区域中央的正方形内，参数设置为：A=1.0，B=0.01，DA:DB:DC=1.0:0.75:0.05，K=1.1×10-12，C*=0.01，D*=0.00978，cr=0.80。

5.2.2 模拟结果

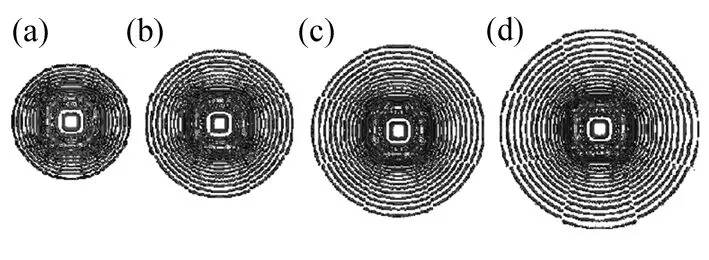
图2 模拟Liesegang图案的形成过程模拟时间t的单位为1。(a) t=200；(b) t= 400；(c) t=700；(d) t=1000。

图2为模拟Liesegang图案的形成过程。在同一时间段，正方形边方向的沉淀带形成更早些(图2(b))，每个角分别对应两条由于沉淀带错位形成的径向断裂;随着时间的进行，错位越明显。模拟结果很好地重现了实验图案的形成。

6 Liesegang图案结果分析

对实验和模拟得到的Liesegang图案分别使用Image-Pro Plus软件和Matlab软件进行图像处理，利用Origin软件进行图像数据分析，验证其沉淀图案是否遵循空间定律和时间定律。

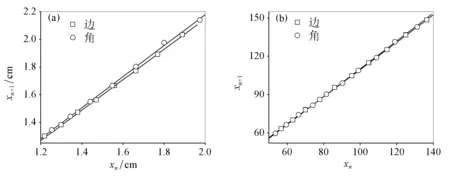
图3 实验和模拟Liesegang沉淀图案的空间定律分析(a) 图1(d)中边角方向沉淀带位置xn+1与xn的线性关系;(b) 图2(d)中边角方向沉淀带位置xn+1与xn的线性关系。

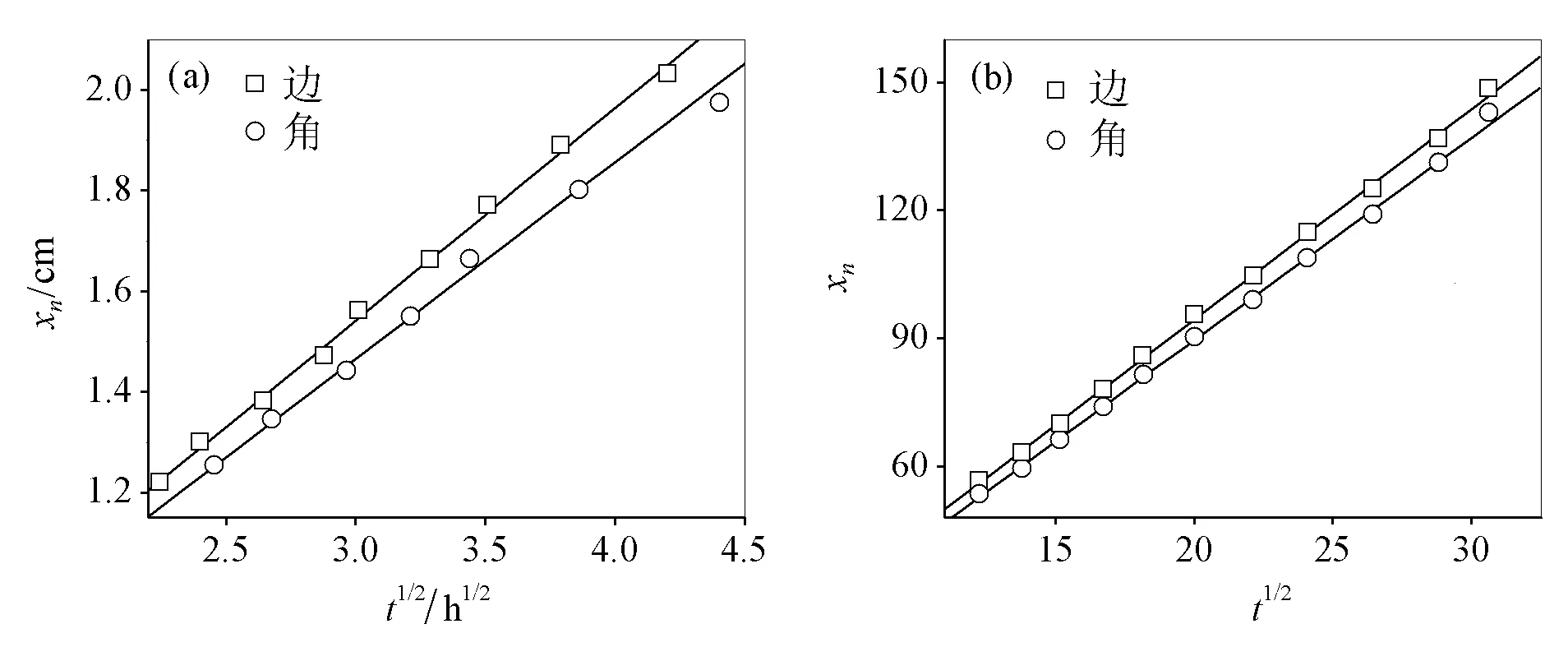
图4 实验和模拟Liesegang沉淀图案的时间定律分析(a) 图1(d)中边角方向沉淀带位置与形成时间平方根的线性关系;(b) 图2(d)中边角方向沉淀带位置与形成时间平方根的线性关系。

图3为实验和模拟形成的Liesegang沉淀图案的空间定律分析。在图3(a)(实验)和图3(b)(模拟)中，xn+1与xn关系曲线均呈直线，表明沉淀带位置xn+1与xn比值为一常数，遵循空间定律。

图4为实验和模拟形成的Liesegang沉淀图案的时间定律分析。在图4(a)(实验)和图4(b)(模拟)中，xn与t1/2之间均呈线性关系，表明沉淀带位置与形成时间的平方根成正比，遵循时间定律。

7 教学成效

本实验作为一个典型的综合性无机与分析化学实验，已经进行了3年(2006～2008年) 教学实践。在指导教师讲解Liesegang图案实验原理和应用价值基础上，学生根据实验要求查阅相关文献资料，自主拟定实验方案，先假设后实验，最后对实验结果进行数值模拟和理论分析。通过这一过程，学生不仅能了解科学研究的基本步骤，加深对沉淀平衡的理解，还能提高综合分析能力。由于Liesegang图案形成与浓度、温度、器皿形状等多种因素有关，实验条件的差异导致得到的实验现象不尽相同，这有助于激发学生探索实验的兴趣。

[1] Liesegang R E.Naturwiss.Wochenschr,1896,11:353

[2] Krug H-J,Brandtstadter H.JPhysChemA,1999,103(39):7811

[3] Peng Q,Wu J G,Soloway R D,etal.Biospectroscopy,1997,3(3):195

[4] Al-Ghoul M,Sultan R.JPhysChemA,2001,105(34):8053

[5] Ostwald W.Lehrbuch der allgemeinen Chemie.Engelmann:Leipzig,1897

[6] Flicker M,Ross J.JChemPhys,1974,60(9):3458

[7] Zheng J H,Wang Q,Wang H,etal.ChinJChem,2008,26(3):433