掠地弹全弹道速度测量数据处理方法

张 焱,卫青春,周 健,赵华敏

(1.西安电子科技大学,陕西西安710071;2.中国电子科技集团公司第五十四研究所,河北石家庄050081;3.遥感信息研究所,北京100192)

0 引言

全弹道速度测量是为了测量掠地飞行的火箭弹及炮弹等高速飞行目标在各个环节的瞬态飞行参数,提供给型号研制单位作全面细致的分析。全弹道速度测量在武器系统精度鉴定及产品统计检验工作中具有重要意义。可以说,武器系统的精度分析[1]离不开测量数据,通过这些测量数据可以分析武器系统的各种参数、特性,并将结果直接应用于武器系统。

对单一初速测量而言,数据处理的特点是只要测量出口后一段短距离弹道参数即可。压力、风向、空气密度和温度等因素对运动学模型影响较小,数据干扰少,数据处理建模和计算方法相对简单。而对全弹道速度测量来说,由于目标的飞行轨迹在不同飞行段的动力学模型不同,所受到的环境影响不同,需要对轨迹进行弹道拐点分段,然后对各个弹道段分别建立数据处理模型。

1 弹道运动规律的动力学分析

以掠地飞行的火箭弹为研究对象,根据动力学分析其弹体飞行弹迹可分为3段:初速飞行段、火箭点火加速飞行段和火箭关机后惯性飞行段。

火箭弹经火炮发射在炮口获得最大速度v0后受空气阻力影响减速飞行,即初速飞行段。经过一段时间飞行后火箭发动机点火,则弹体获得正加速度推力,即进入点火加速飞行段。随后发动机关机由于受空气阻力影响会产生负加速度,进入关机惯性飞行段。

基于对弹道运动学的初步分析,弹体运动的速度曲线如图1所示。

在图1中,弹体整个飞行时间段为t0～te,假设多普勒信号经A/D采样和FFT谱分析计算后,给出m组弹道测速数据,采样间隔为h,则在采样时间间隔ti=ih时刻,弹道对应速度数据vi,每一组(ti,vi),i=1,2,…,m构成要处理的弹道数据序列。在对全弹道数据进行处理时需要将测量数据分段,此时就需要获取火箭开、关机时刻,即图1中ts、tc的值。可以采用判断加速度拐点发生时刻的方法分离出火箭开、关机时刻。

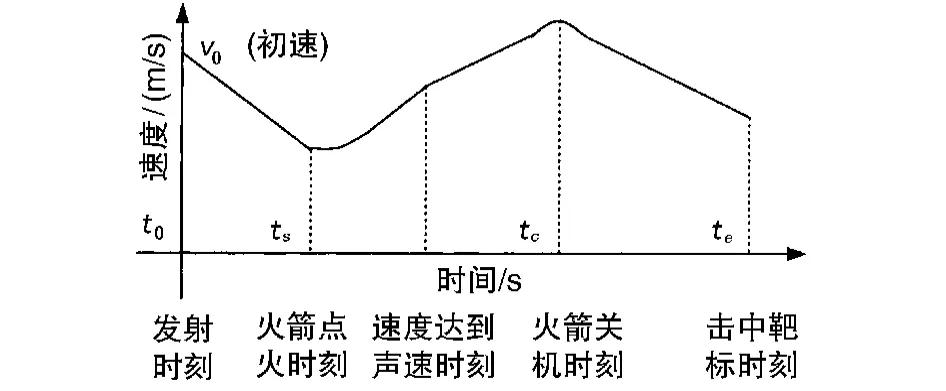
图1 全弹道运动模型速度曲线

2 不同弹道段数学模型的确定

由于各种原因,测量数据总含有随机误差,必须通过相应的平滑与滤波处理,减少随机误差的影响[2]。不同的弹道段往往要采取不同的处理方法才能达到较好的处理结果[3]。

依据火箭弹动力学规律,不同弹道段对应不同运动方程,但弹道运动方程在每时刻测量值模式可统一表述为:

式中,vi为速度测量值;ti为速度测量时刻;εi为测量噪声误差,i=1,2,…,N。

不同的弹道段对应的多项式阶数p不同,系数a0,a1,a2,…,ap也不同,为此要依据测量数据,确定不同弹道段的多项式阶数p和系数aj,j=0,1,…,p。

2.1 多项式次数确定

通过变量差分法分别确定3段弹道的多项式次数。由变量差分法知,在每个弹道段当差分次数大于等于对应的多项式阶数p时,速度测量值的差分序列中不再含测量数据的真实信息,仅含有随机误差成分,均方差估计量统计Sp,Sp+1,Sp+2,…趋于定值,有如下关系式成立:

因此,对每个弹道段求Si的下列比值δi:

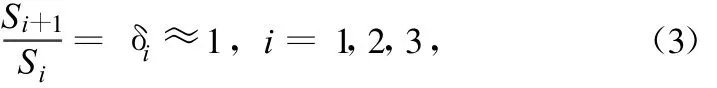
即 δi近似等于1,如满足0.9≤δi≤1.1,则可确定该段弹道运动方程的多项式阶数为:

该段弹道数据的统计均方差,即标准差为:

针对公共安全服务供给矛盾的问题，国内学者也提出不同的看法。 一方面，有些学者对社区公共服务供给的适用理论进行了充分探讨，陈伟东和李雪萍这两位学者则将多中心治理理论运用到了城市社区研究领域，提出了社区公共产品供给多主体秩序理论[3]； 宋世明在《工业化国家公共服务市场化对中国行政改革的启示》一文中强调： 应把公共服务的市场化纳入到中国行政改革的实践框架中，这是符合配置政府权威制度与市场交换制度的功能优势的需要，这是遵循公共服务供给规律的客观需要，同样是提高政府能力的必然选择。[4]

2.2 多项式系数确定

当每段测量数据 vi,i=1,2,…,N,N值在3段弹道中分别对应值为Z、W 、L,且N ≥p时,弹道运动方程可表示为矩阵形式为:

式中,

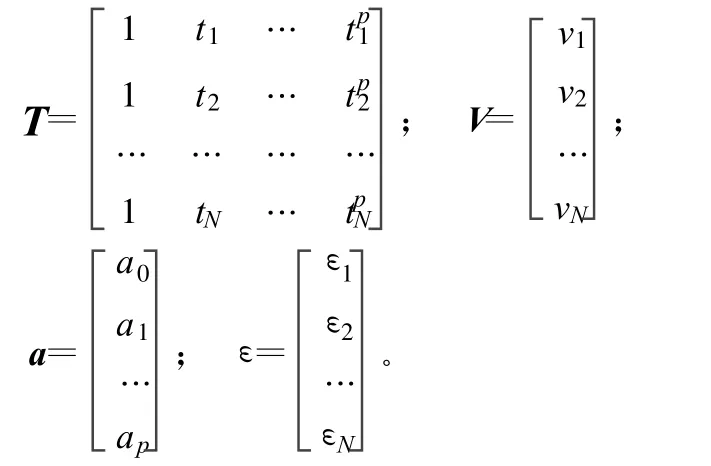
由最小二乘法估计可得到多项式系数向量a的估计值为:

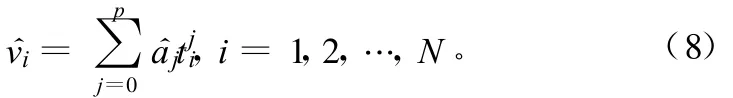
因此得到每个弹道段的数学模型,根据该数据模型可进行数据的野值剔除和平滑、滤波等工作。

3 径向速度修正与数据融合

为了获取更高精度的测速数据,需要在平滑、滤波的基础上进行进一步处理。

3.1 径向速度修正

由于弹道雷达部署在火箭弹发射装置的侧翼,因此测到的径向速度 vi要通过换算才能得到弹头相对发射装置的弹道切线速度vri。

弹头在弹道上飞行的瞬时距离为:

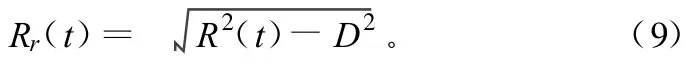
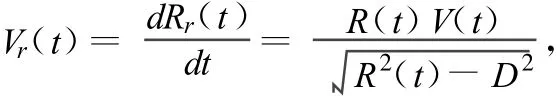
即

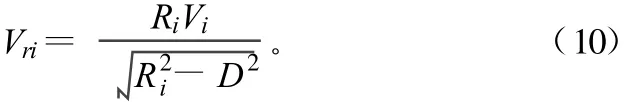
式中,D为弹道雷达到发射装置射向中心的捷径。实际应用时,要将式中Vi用平滑后的速度数据^Vi取代,Ri要通过对^Vi的数字积分获得。

3.2 数据融合

火箭在初速飞行段由初速雷达和弹道测速雷达同时测量,假设时标对齐后2部雷达测得的速度数据换算为射向线速度序列分别为,通过对初速飞行段的残差统计分析,可获得2部雷达在初速段测速数据的方差估计,假设经估计的结果分别为和,将2部雷达测得数据融合在一起,数据的精度可得到进一步提高。速度融合公式为:

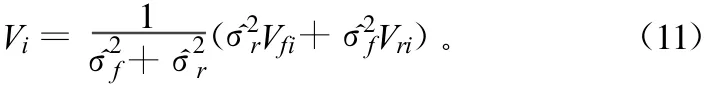
4 软件实现及试验验证

采用上述数据处理方法开发了全弹道测速数据处理软件。数据处理软件采用Visual C++和Matlab混合开发。将二者混合编程,是一种有效的编程方式。将Matlab的以矩阵为基本编程单位的高效数值计算语言与VC++程序文件小、执行速度快、实时性好的特点有效地结合,显著提高了软件的开发效率与运行效率[4]。

具体实现上采用VC++进行程序主体框架的开发,通过Matlab引擎直接调用Matlab内嵌函数完成数据的平滑、滤波等算法实现。完成后的数据处理软件流程如图2所示。

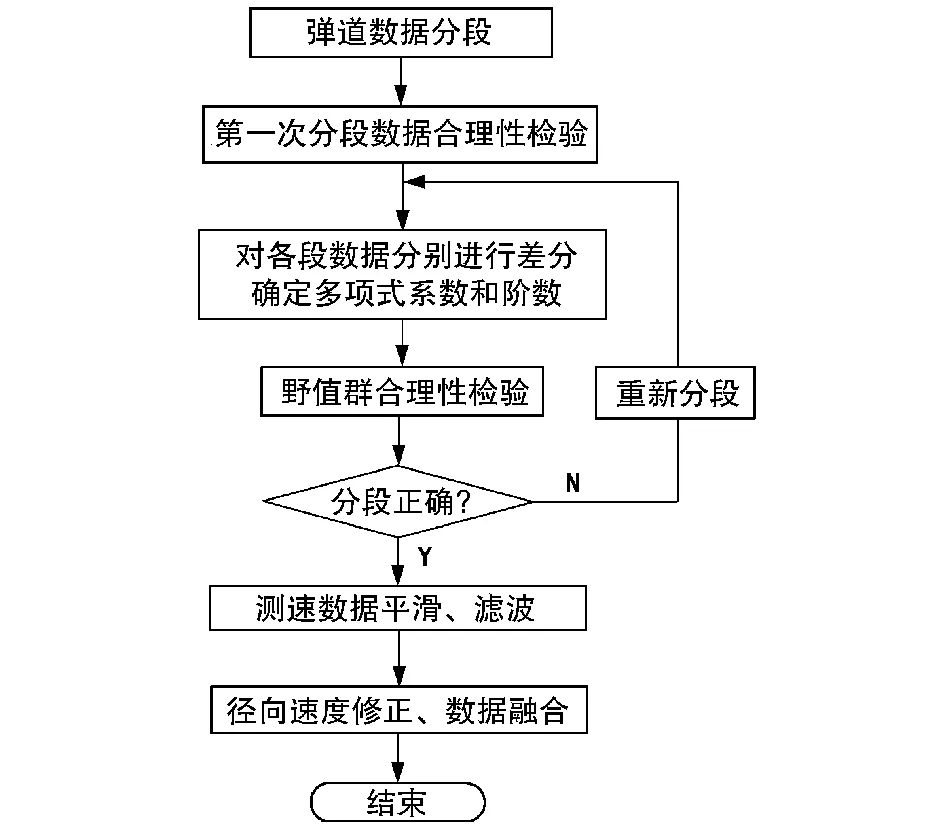
图2 数据处理软件流程

数据处理软件配合全弹道测速雷达系统参加了某型号反坦克火箭弹实弹射击试验。火箭弹加速飞行段的时间—速度曲线图如图3所示。

图3(a)为加速飞行段原始数据,含有野值、野值群,共有15点野值。图3(b)为经合理性检验后数据,从图中可以看出野值及野值群已被剔除。图3(c)为经平滑滤波后数据,数据经平滑后曲线变得光滑。

经合理性检验和平滑、滤波之后的数据同之前统计均方差之比为:μ=0.128 3,1/μ=7.79。即经平滑滤波数据处理后,测量速度的数据精度提高了7.79倍。

图3 时间—速度曲线图

5 结束语

根据掠地火箭弹运动规律分析结果建立弹道数据模型,基于分段处理的思路进行全弹道测速数据处理。在具体处理中采用了正交多项式进行平滑、滤波、预测及数据合理性检验,并通过径向速度修正和数据融合进行综合处理。据此开发的数据处理软件对实弹射击采集数据进行了处理,获得了较高的数据精度,取得满意效果,具有较好的工程意义。

[1]张锦斌,马万权,黄 巍,等.运用卡尔曼滤波理论求解测速雷达系统误差[J].飞行器测控学报,2000,19(4):80-88.

[2]华师韩,王 青.数字滤波在动态测量数据处理中的应用[J].宇航计测技术,2005,25(2):50-54.

[3]唐宏斌,郑 键,李 骏.主动段弹道估计可观测性分析[J].电子信息对杭技术,2006,21(2):27-31.

[4]陈路路.VC++和Matlab集成应用的研究[J].无线电工程,2006,36(1):55-58.