变形矩形脊波导传输特性分析

赵 霞,陈小强

(兰州交通大学自动化与电气工程学院,甘肃兰州730070)

0 引言

在现代微波技术中,为了满足微波传输系统的某些要求,需要不断探索和研究具有特殊截面形状的各种新型波导。研究分析表明,脊波导与矩形波导相比有着主模截止波长较长、单模工作频带较宽等优点[1],这使得脊波导在微波和毫米波的器件中得到广泛的应用。目前,除了对单脊波导的研究,还有双脊波导和背脊波导等[2-5]。在生产实际中,由于生产制造、装配及使用等原因,可能会造成脊波导的变形,分析研究变形对脊波导传输特性的影响,有助于更科学、更精确地分析微波器件和由脊波导构成的微波系统的特性。下面主要研究矩形单脊波导在错位变形和不同受力变形情况下的传输特性。

1 理论分析

假设脊波导内为空气且纵向均匀,采用纵向场法,脊波导内的场结构可以归结为求解亥姆霍兹(Helmholtz)方程:

2 数值计算结果

2.1 波导错位变形的计算

根据现有资料分析结论,取传输特性较优时几何尺寸,并便于与文献[7]对照,选择波导几何尺寸如下:矩形单脊波导的宽边为a,窄边为b=0.45a,边s=0.5a,边d=0.5b。变形程度选取不超过宽边的10%,所以取变形角度 φ=0°～13°,保证了变形在10%以内。

根据上述分析,对脊波导及错变脊波导TE波的TE10模及邻近高次模的特征值进行求解,求出不同变形程度时主模及邻近高次模的截止波长,计算了单模带宽。错位变形脊波导的归一化主模截止波长 λc/a及单模带宽λc1/λc2的变化曲线如图1所示。矩形单脊波导错变归一化截止波长和单模带宽的相对误差如表1和表2所示。

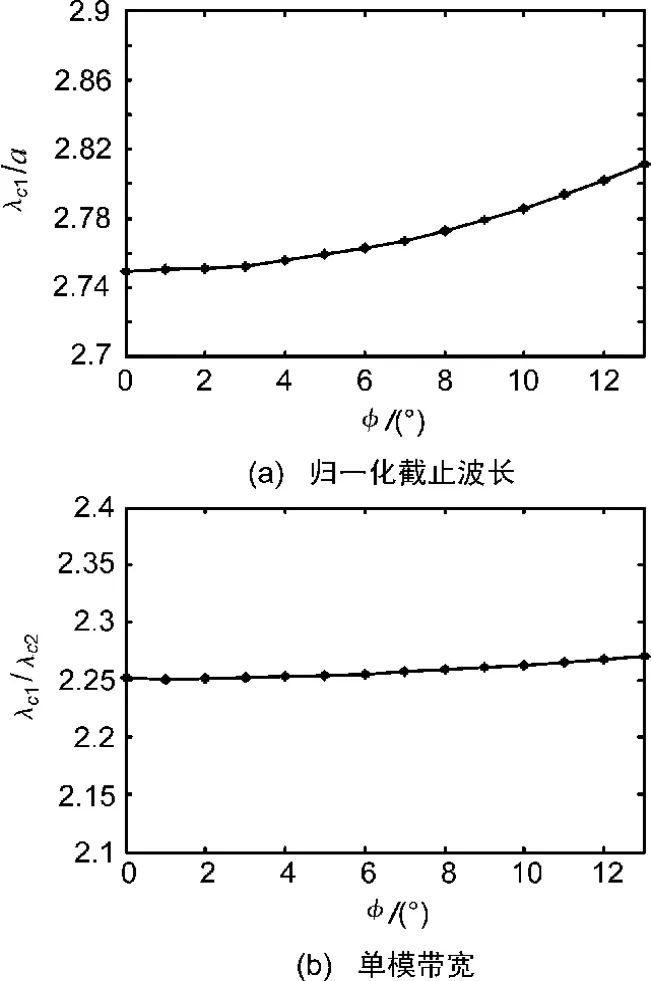
图1 错变脊波导的传输特性

表1 脊波导错变归一化截止波长的相对误差

表2 脊波导错变单模带宽的相对误差

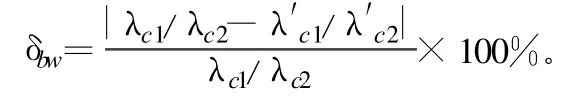
式中,λc为未变形时的截止波长;λcd为变形后的截止波长;λc1/ λc2为未变形时的单模带宽为变形后的单模带宽。

取变形角度 φ=0°、5°和 13°时主模电场结构图如图2所示。

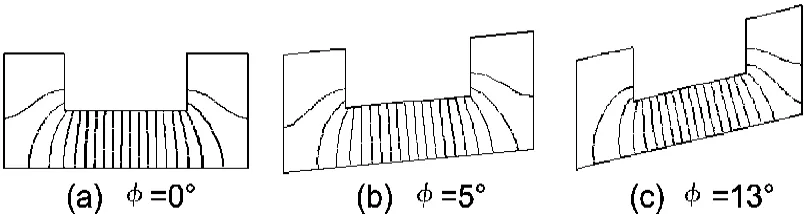
图2 错位变形场结构图

2.2 单脊波导受力变形计算

单脊波导尺寸的选择如上所述,变形程度σ=(0.01-0.1)a。

矩形单脊波导受力变形如图3所示,脊波导受力后产生变形,对受力变形脊波导TE波的TE10模及邻近高次模的特征值进行求解,求出不同变形程度时主模及邻近高次模的截止波长λc/a,得到单模带宽λc1/λc2。矩形单脊波导受力各种变形归一化截止波长的相对误差如表3所示,矩形单脊波导受力各种变形单模带宽的相对误差如表4所示。脊波导受力变形的主模归一化截止波长及单模带宽λ/c1λc2的变化曲线如图4所示。取变形程度σ=0.02a时主模电场结构图如图5所示。

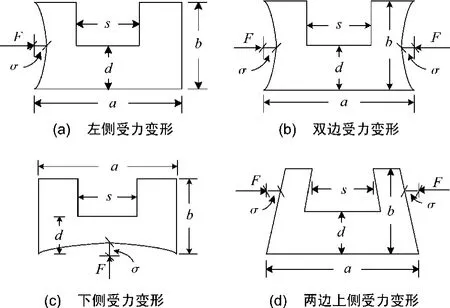
图3 矩形单脊波导受力变形

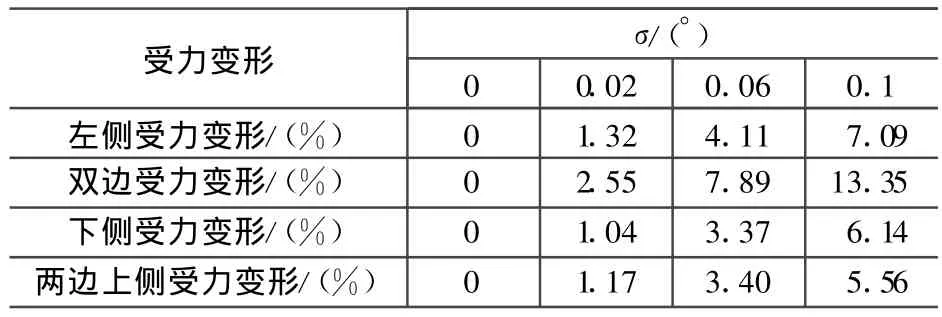
表3 脊波导受力变形归一化截止波长相对误差

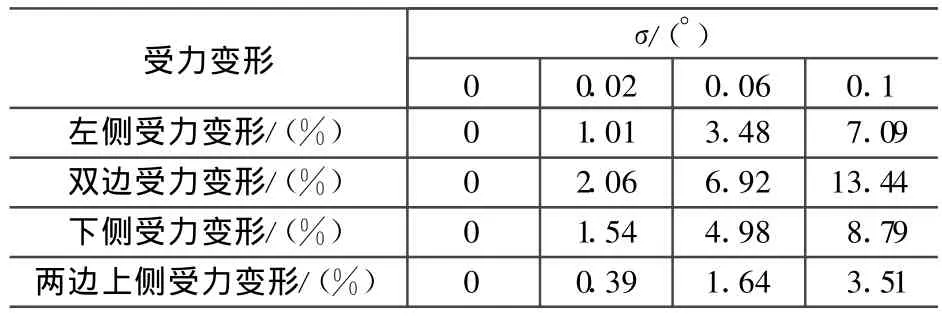
表4 脊波导受力变形单模带宽相对误差

图4 受力变形脊波导的传输特性

图5 受力变形场结构

3 结果分析

通过对矩形脊波导变形后的传输特性分析,得出以下结论:

①矩形单脊波导错变后的归一化截止波长随着变形程度的增大而增大,当变形达到10%时,其相对误差为+2.26%;

②矩形单脊波导错位变形的单模带宽随变形的增大呈增大趋势,当变形达到10%时,其相对误差为0.8%;

③矩形单脊波导受力变形后,在图3(a)、图3(b)和图3(d)所示的变形中,随着受力增大,变形程度增大,归一化截止波长和单模带宽都在减小,在图3(c)所示的变形中,随着受力增大,变形程度增加,归一化截止波长和单模带宽都在增大,其中图3(b)的归一化截止波长和单模带宽的相对误差最大,当变形达到10%,其相对误差分别为13.35%和13.44%,表明当矩形单脊波导受到如图3(b)所示力变形时,对其传输特性影响最大,特性变差,是应该避免的情况,而图3(c)的受力情况使特性变好,应用时可以不考虑这种变形的影响;

④脊波导错变后,传输特性的变化较小,与没有受力变形时相比,相对误差在5%以内,在工程上可以接受;

⑤主模的电力线在矩形脊的顶部比较集中。

4 结束语

以上分析表明,对于矩形单脊波导,应用时应尽量避免双边同时受力,如图3(b)所示的情况;对于受力如图3(c)的情况,可不考虑对传输特性的影响。在工程应用中,对于错变的情况,只要变形在工程允许的范围内,其对传输特性归一化截止波长和单模带宽的影响可以不考虑。但对不同的受力变形,只要保证变形程度不超过8%时,可保证工程实际应用的需要。

[1]PYLE J R.The Cutoff Wavelength of the TEl0Mode in Ridged Rectangular Waveguide of any Aspect Ratio[J].IEEE Trans.MTT,1966,14(4):175-183.

[2]MAI Lu,LEONARD P J.Dependence of Ridge Position on the Cutoff Wavelength of the Dominant Mode in Single Ridge Waveguides[J].Microwave and Optical Technology Letters,2002,34(5):371-374.

[3]RONG Y,ZAKI K A.Characteristics ofGeneralized Rectangular and Circular Ridge Waveguides[C].IEEE Trans.MTT,2000:258-265.

[4]HOPPER S.The Design of Ridged Waveguides[J].IRE Trans.,1955(MTT-3):20-29.

[5]黄彩华.矩形变形脊波导主模截止波长和特性阻抗计算[J].雷达与对抗,1997(3):16-22.

[6]金建铭.电磁场有限元分析[M].西安:西安电子科技大学出版社,2001.