有向天线圆阵对椭圆极化信号的测向方法

杨 松,李艳斌,李 淳

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

信号的波达方向(DOA)估计是空间谱估计的一个重要研究内容,由于有向天线阵列对波束范围内的信号增益比较大,具有比较理想的测向效果,尤其适合对微弱信号的测向,因此其应用范围非常广泛,研究有向阵列的测向问题具有重大的理论和现实意义。极化矢量是信号的一个重要参量,它包含了信号的极化信息,许多问题都可以从极化入手。这里主要研究均匀圆阵对椭圆极化波的测向问题。

1 问题分析和接收信号模型

1.1 对信号的极化分解

依据信号在空间内建立坐标系,将信号传播方向(圆阵中心与信源的连线方向)在天线阵列所在平面上的投影作为Y轴,与Y轴垂直的方向作为X轴,垂直天线阵列所在平面向上的方向作为 Z轴,如图1所示。

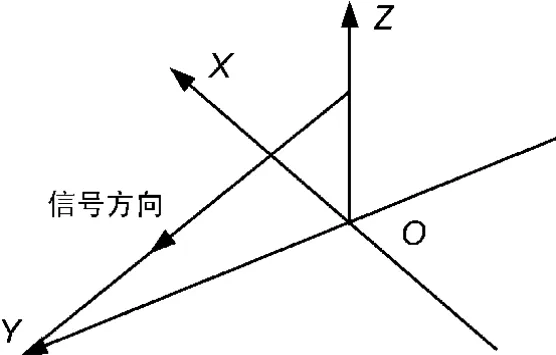
图1 极化分解示意图

将信号的瞬时极化向量在3个坐标轴上分解,得到3个线极化信号,这些信号传播方向不变,极化方向分别是3个坐标轴方向。由于组阵所用天线为水平极化天线,因此Z轴极化的信号分量在天线阵列上没有响应,其余2个信号分量有响应,但天线阵列对它们的增益不同,设天线阵列对X轴极化的信号分量和Y轴极化的信号分量的增益分别为ci和di(i=1,……,m)。设极化椭圆在信号到达第1个阵元时的相位为 xw1,显然它是一个时变的量。设极化椭圆的倾角为τ,极化率角为ε,信号的方位角为θ(信号方向在天线阵列所在平面的投影与某固定方向的夹角),俯仰角为 φ(信号方向与天线阵列所在平面夹角)。阵列结构示意图如图2所示。

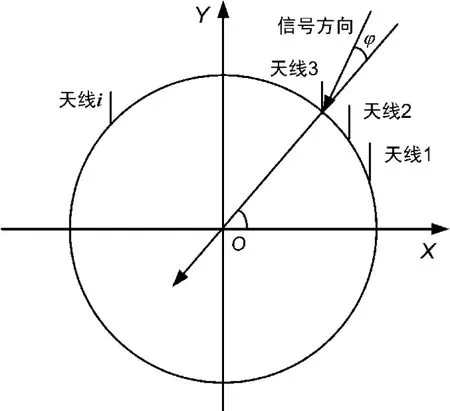
图2 阵列结构示意图

于是可以得到信号到达各个阵元时的初始相位为:

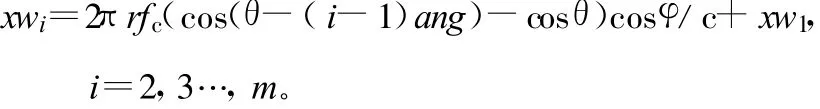
式中,r为圆阵半径;fc为信号中心频率;ang为相邻2个天线之间的夹角。设极化椭圆的长轴和短轴构成的直角三角形的斜边长为1,进而得到信号的瞬时极化分量在X轴、Y轴、Z轴上的分量大小分别为:

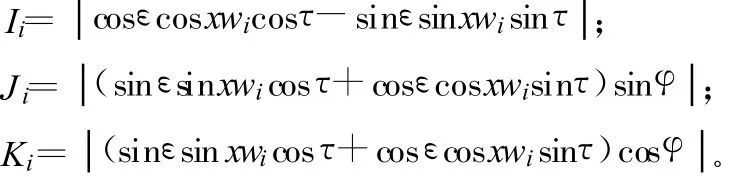
式中,i=1,……,m,表示阵元序号。

1.2 阵列对信号的接收模型

由于信号能量随时间变化相对稳定,故各分量的归一化结果分别为和,于是此时各个阵元的接收为:

式中,sigi表示第i个阵元的相位突变判决符号,取0表示相位无突变,取1表示相位有突变;j为虚数单位;S(t)表示信号;N(t)表示噪声;wi为第i个阵元相对圆心的相位差,

wi=2πrfccos(θ-(i-1)ang)cosφ/c。

2 基于增益比估计的MUSIC算法

对Xi(t)进行化简得:

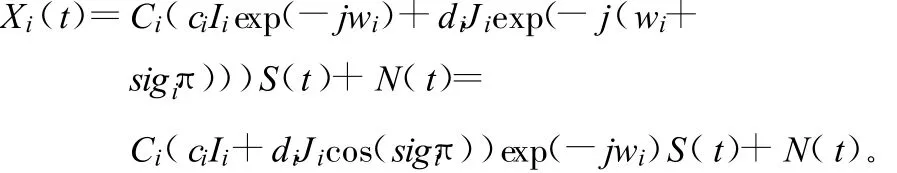
由于阵列流型前各阵元的系数不同,接下来设法由接收数据获得各阵元的增益比信息,进而用MUSIC算法进行求解。先观察系数的构成,即Ci(cicji+didjicos(sigiπ)),i=1,……,m,其中只有xwi(可归结到 xw1)这一项是时变量,剩下的参量都只与阵元序号有关。xw1随时间t变化关系如下:

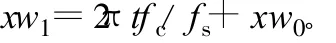
式中,xw0为初始时刻的极化相位。

2.1 数据分选

要完全消除xw1随时间t变化对增益比的估计造成的影响是不可能的,只能尽量减小它的影响。而为使用MUSIC算法,又需要多组含有相近增益信息的数据。先定义一个足够小的区间,使xw1在该区间内变化对增益造成的影响足够小,从而不至于导致后续步骤产生过大误差。由 xw1=2πtfc/fs+xw0可筛选出 xw1在哪些时刻落入选定的区间,从而确定一组时刻序列,然后用这组序列对数据进行筛选,获取一组新的数据,这组数据包含的各阵元增益不再随时间产生很大的变动,而是相对稳定。

2.2 增益比估计

现在求解各个阵元的增益比。先将该问题进行简化:未知正增益 z1、z2、……、zm,未知信号 s和噪声n1、n2、……、nm均为行向量,但噪声与信号、噪声与噪声之间相互独立,且噪声零均值并具有相同的方差,记为σ2,信号均方值记为J。得到接收数据为:

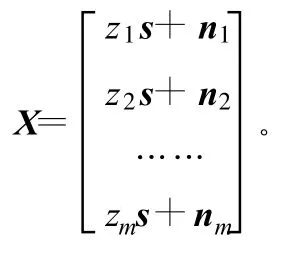
求解z1:z2:……:zm。

解决方案如下:求X的相关矩阵Y=XXT/m,对Y进行化简得:

从而取Y(1,1)、对角元 Y(p,p)以及Y(1,p)就可以解出z1:zp,其中2≤p≤m。

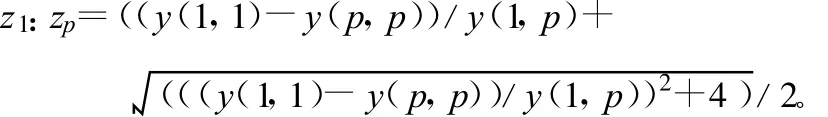
重复进行即可求出z1:z2:……:zm。

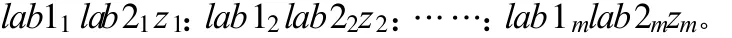
2.3 基于增益比估计的MUSIC算法

窄带远场信号的数学模型为:

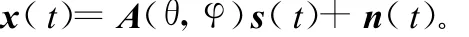
阵列数据的协方差矩阵为:

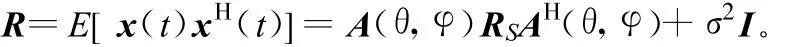
式中,RS为信号的协方差矩阵,由于信号与噪声相互独立,数据协方差矩阵可分解为与信号、噪声相关的2个部分 ,A(θ,φ)RSAH(θ,φ)为信号部分 ,对 R进行特征分解有:

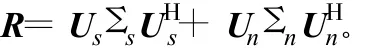
式中,Us是由大特征值对应的特征向量矩阵,其列向量张成信号子空间;而 Un为小的特征值对应的特征向量矩阵,其列向量张成噪声子空间。这里的信号子空间和噪声子空间实际上就是接收数据协方差矩阵的列空间和零空间,由矩阵理论可知二者相互正交。又由于窄带信号的包络在阵列孔径过渡时间内可以认为是近似不变的,所以阵列对来波方向为(θ,φ)的信号的采样快拍向量为:

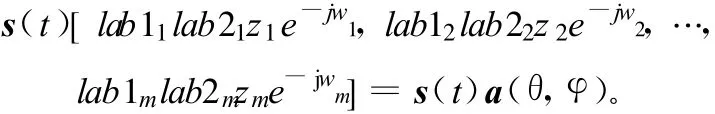
于是信号子空间可以认为是由a(θ,φ)张成,即Us的列向量张成的空间与a(θ,φ)张成的空间是一样的 ,都是信号子空间,所以 a(θ,φ)与 Un正交 ,即

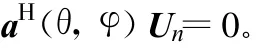
定义空间谱函数为:

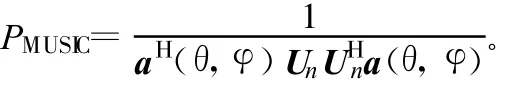
从而通过谱峰搜索来对来波方向进行估计。

3 仿真实现

仿真结果如表1所示。仿真用信号为FM信号,信噪比为0 dB,带通采样频率为80 kHz。

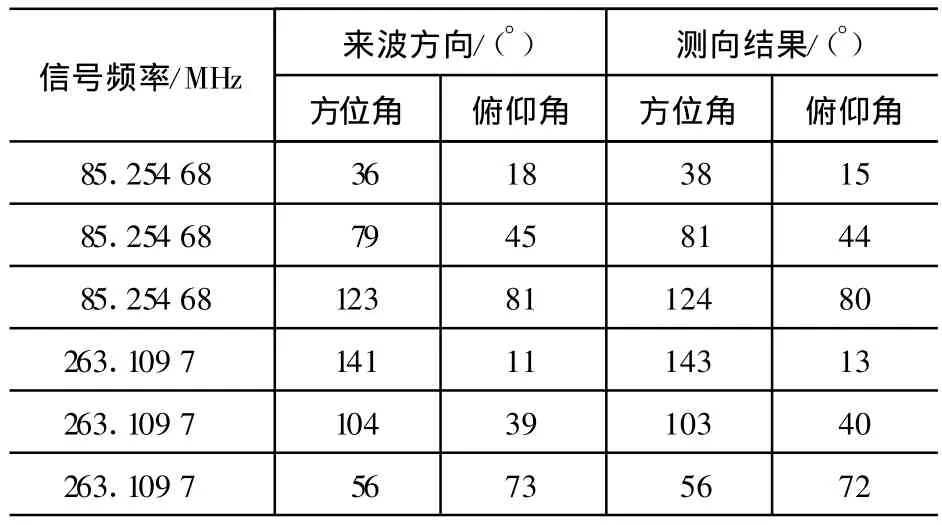
表1 仿真结果

从表中可以看出,测向准确度较高,在信号信噪比为0 dB的情况下测向误差一般不超过2°。其中信号频率为263.109 7 MHz,来波方向方位角为104°、俯仰角为39°时的测向结果如图3所示。

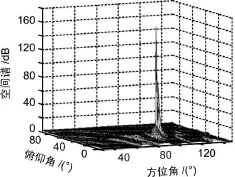
图3 仿真结果

从图中可以看出,当俯仰角大于80°时,方向角已经不太好判断。这其实是有现实依据的,当俯仰角很大时,方向角确实已经很模糊,不好判断,直至到达90°,此时已经完全无法分辨方向角。这也从一个侧面说明了仿真的正确性,更加印证了算法的可靠性。

4 结束语

在对信号极化分解的基础上,建立了信号接收模型,并基于增益比估计用MUSIC算法对模型进行了求解。通过仿真实验验证了算法的可行性,并且达到了较高的测向精度,在理论上较好地解决了有向天线阵列对椭圆极化信号的测向问题。当然,实际情况要比建立的模型复杂得多,解决工程实践问题还要结合实际情况具体分析。另外,算法运算量较大,数据利用率不高的问题还需进一步改善。

[1]徐振海.极化敏感阵列信号处理的研究[D].长沙:国防科技大学博士论文,2004:11-14.

[2]刘 刚,吕新华,攸 阳.阵列信号处理中基于MUSIC算法的空间谱估计[J].微计算机信息,2006,22(4):302-304.

[3]李炳荣,曲长文,平殿发.基于MUSIC算法的圆阵测向技术研究[J].弹箭与制导学报,2007,27(1):207-210.

[4]魏 亮,段召亮,赵 胜.基于L型阵列的MUSIC二维估计算法研究[J].无线电工程,2010,40(8):32-33.