大点数FFT设计中提高资源利用率的方法

李 斌,田素雷,孙雪晶

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

快速傅里叶变换作为时域和频域转换的基本运算,是频谱分析的必要前提,在数字通信、语音信号分析、图象处理、雷达、地震和生物医学工程等数字信号处理领域有着极为广泛的应用。

随着数字信号处理技术的飞速发展,应用系统对于高速大点数的FFT处理器需求越来越大,这就意味着芯片的资源、面积、功耗和成本都将大幅提高。在目前FFT算法已经相当成熟的条件下,系统运算量难以减少,因此只能通过改善实现方式,即增加资源,提高并行度,提高工作频率,才能达到更高的变换速度。

该文介绍了2种用于提高大点数FFT设计中资源利用率的方法,通过提高运算单元和存储单元的利用率,能够有效地减少变换时间和资源面积。以一个64 K点FFT处理器的设计为例,对2种方法进行了详细分析。

1 FFT算法

FFT算法的基本思想:利用WNr函数(旋转因子)的周期性、对称性,将原有的N点序列分解成2个或者多个较短的序列,这些短序列的傅里叶变换(DFT)可以重新组合成原序列的DFT,并且总的运算次数比直接的DFT运算次数少的多,从而达到提高速度的目的。

长度为N的FFT变换可以写为:

式中,k,n∈[0,N-1],N为运算点数。

由FFT算法可知,基数越高,总运算量越少,因此采用高基数的蝶形运算方式,能够提高运算速度。基16按时域抽取(DIT)可以写为:

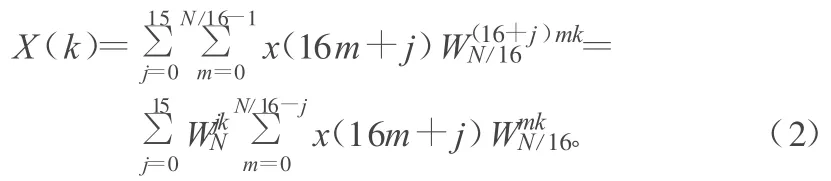
式中,m∈[0,N/16-1];j∈[0,15];k∈[0,N-1],N为运算点数。

令

式中,i∈[0,15]。

观察Yi可知,Yi为N/16点的FFT运算,可以将N点降为N/16点的FFT运算。

而式(2)按照基16分解为 x(16m),x(16m+1),x(16m+2),…,x(16m+15)分别抽取,可以分解为:

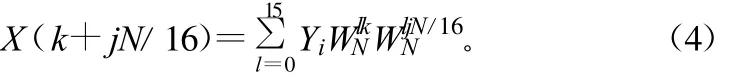
式中,X(k+jN/16)表示基16运算的第 j个输出点,而Yi则可以通过N/16点FFT来实现,从而实现迭代运算。

2 提高运算单元的利用率

传统的FFT变换分为3个阶段,首先将输入数据全部存入RAM,之后进行各级蝶形运算,蝶形运算全部完成后再从RAM中输出数据,这样运算一组数据需要的时间即为(载入时间+运算时间+输出时间)。

在这种载入、运算和输出顺序进行的结构中,只有数据全部输入后运算单元才开始工作,同样,只有运算全部结束后才能进行数据输出。这样在大点数FFT变换中,输入输出会占用大量时间,而此时运算单元则处于空闲状态。因此,对变换过程进行了改进,将输入的部分数据与运算数据重叠,输出的部分数据也可与运算数据重叠,使得运算单元能够在数据输入或输出的同时进行运算,减少其在整个变换过程中的空闲时间。

按照蝶形算法的运算顺序,在一组数据的FFT运算中,当第k级的运算进行到第n=3×4(s-k-1)=3N/4(k+1)(s为运算N个数据的FFT所需要的总级数)个数据时,第k+1级运算即可开始。根据这一特点,变换过程的“载入-变换-输出”3个阶段可以进行重叠,既输入的同时进行第1级蝶算,第4级蝶算的同时进行输出。

受到FFT算法的限制,运算和输出重叠的条件是变换结果倒序输出。如果需要正序输出结果,那么最后一级运算结束之后才能够进行输出。输入和运算重叠则没有条件限制。

以64 K点的FFT为例,此设计采用的是16输入的基16蝶形运算,共需4级,每级4 K个时钟周期的运算时间。不同阶段变换的重叠部分示意图如图1所示。

对于一组64 K点数据的FFT变换,由于数据按时钟采样取数,所以64 K个数据需要64 K个时钟周期来完成输入,根据算法,第1级蝶算需要的数据为 n,n+4 K,n+8 K,…,n+56 K,n+60 K(n∈[0,4 095]),因此输入到第60 K个数据时,就可以开始进行第1级蝶算,即当64 K数据输入完成时,数据的第1级运算也随之完成。这样,载入和变换可以有4 K个时钟周期的重叠时间,如图1(a)所示。

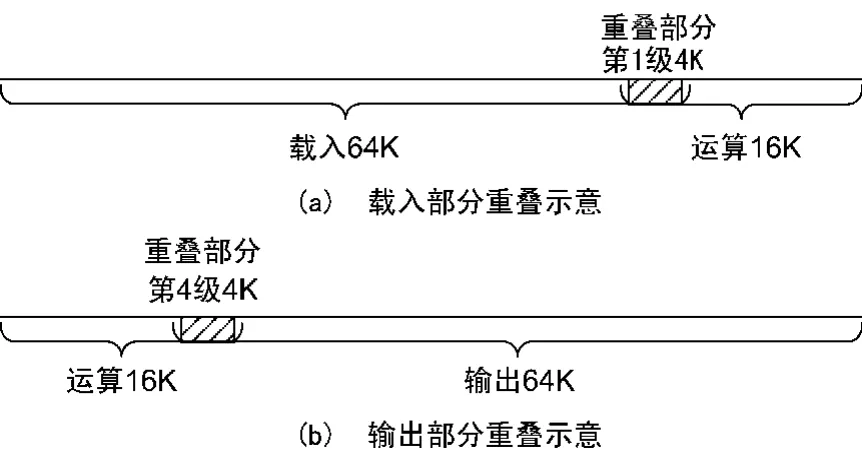
图1 不同阶段重叠的变换示意图

输出时采用数据倒序输出。根据蝶算单元中基4倒序输出的规律,当第4级蝶算每时钟周期产生16个变换结果时,将这16个结果数据中的第1个直接进行输出,其余数据仍存放回原位置。完成第4级蝶算共需要4 K个时钟周期,可以输出4 K个数据,这样就实现了边运算边输出,变换和输出有了4 K个时钟周期的重叠,如图1(b)所示。

3 提高存储单元的利用率

受限于FFT算法本身,要提高数据吞吐率最好的方法就是多组数据之间采用流水实现连续的运算,在实际应用中,系统也往往需要FFT模块具有连续运算的能力。常见的方法是通过3倍的乒乓随机存储器(RAM)来实现流水线,但对于大点数设计,这样会造成电路规模和面积的大幅增加。为减少不必要的资源占用,可以通过RAM的循环使用来实现流水设计,只需增加部分RAM进行缓冲,就能达到数据连续变换的目的。

下面同样以64 K点的FFT设计来进行详细介绍。设计中使用了必需的4组RAM,每组16 K,以及部分缓冲RAM。

载入时RAM整体使用示意图如图2所示,斜线表示未运算数据,方格表示正在进行运算的数据。4个子图中每个标准矩形表示1组4块的4 K×32的SRAM。图2(a)表示第1次载入时,前60 K数据载入后RAM的使用情形,这时只有第4组RAM的后1/4(也就是最后一块RAM)是空的,并且没有开始变换。图2(b)表示载入60～64 K数据的情形,这部分数据没有载入到第4组RAM的后1/4(也就是最后一块RAM),而是将直接进行第1级变换,当然,变换的结果需要存入这部分RAM。图2(c)和图2(d)为第2和第3级变换,在这段时间里,数据被载入到第5组进行缓冲的RAM中。

图2 载入时RAM整体使用示意图

输出时RAM使用示意图如图3所示,斜线表示未运算数据,方格表示正在进行运算的数据,网格表示等待输出的数据。

图3 输出时RAM使用示意图

图3(a)和图3(b)中4个较大的矩形表示第1组中的4块RAM,它们内部存放的数据在第4级时都由第1号蝶算单元进行运算。图3(a)表示第1块RAM中的数据运算后不再存回,直接输出,以便新的数据可以载入。每一块RAM的读取都是完全正序的,即按照0,1,2,…,15,…,4 K-1的顺序。由于这4块数据同时参与运算,所以第2、第3和第4块RAM的数据被写回原地址保存。这4块RAM运算完成需要4 K个时钟周期。4块RAM运算完成后,第1块RAM也完全空了,其他3块RAM则装满了变换结果,如图3(b)所示。

图3(c)和图3(d)中4个较大的矩形表示第2、第3和第4组中的任意一组的4块RAM,它们内部存放的数据在第4级时分别由第2、第3和第4号蝶算单元进行运算。图3(c)表示第4级运算正在进行中,这些运算和第1组的4块RAM中数据的运算同时进行。每一块RAM的读取都是完全正序的,即按照0,1,2,…,15,…,4 K-1的顺序。运算的结果即变换的结果被写回原地址保存。这4块RAM运算完成也需要4 K个时钟周期。4块RAM运算完成后,都装满了变换结果,等待输出,如图3(d)所示。

第4级运算时,第1组(中的第1块)RAM就可以同时输出数据,也能够够载入新的数据。当第4级运算结束后,第1组RAM开始纯粹的输出。第1组RAM输出完毕后,依次序是第2、第3和第4组 RAM输出。数据输出的存储单元就可以载入新的数据了。

以上是连续变换时,一组数据存储、变换和输出的整个过程。同时上述部分也详细分析了只使用少量RAM就可以实现的连续变换的方法,其核心思想是3个合并:把一组运算数据的输入和其第1级运算合并,把第4级运算和输出合并,把输出和下一组数据的输入合并。这样只需增加少量的RAM就可以实现连续变换,缓冲RAM的大小取决于中间运算需要的时钟周期数。

4 结束语

在并行度、时钟频率和蝶算基数相同的情况下(16输入基16蝶算,流水线运算),未采用文中所述方法时,电路的运算时间为16 K个时钟周期,占用的存储器为192K的SRAM。采用文中所述方法后,电路的运算时间为8 K个时钟周期,占用的存储器为72 K的SRAM。

由此可见,文中的2种提高资源利用率的方法确实有效的减少了变换时间和资源占用。

[1]CHEN Yuan,LIN Yu-wei,TSAO Yu-chi,et al.A 2.4-Gsample/s DVFS FFT Processor forMIMO OFDM Communication Systems[C].IEEE Journal of Solid-state Circuits,2008:1260-1266.

[2]OPPENHEIM A V,WILLSKY A S.Signals and Systems[M].Prentice-Hall,1983.

[3]谭 征,张晓林,杜永久.一种基于FPGA的超高速FFT处理器设计[J].遥测遥控,2005,26(6):46-49.

[4]管吉兴.FFT的FPGA实现[J].无线电工程,2005,35(2):43-46.

[5]程培青.数字信号处理教程[M].北京:清华大学出版社,1995.

[6]赵 鑫.VHDL与数字电路设计[M].北京:机械工业出版社,2005.

[7]高西全,丁玉美,阔永红.数字信号处理-原理、实现及应用[M].北京:电子工业出版社,2006.