磨削硬齿面大内齿圈的椭球形蜗杆砂轮研究

孙洪胜 李宇鹏 张世珍 赵永昌 崔云起 王海艳

(①燕山大学，河北秦皇岛 066004;②北京工研精机有限公司，北京 100102)

用球形或椭球形滚刀加工内齿圈［1－2］解决了制造业中的棘手问题，然而重型装备中的大模数内齿圈是硬齿面，因此探讨磨削大模数硬齿面内齿圈是亟待解决的问题之一。文献［2］提出了球形蜗杆砂轮，给出了球形砂轮的基本参数。但是，若球形砂轮当量齿轮齿数增大，球形砂轮尺寸、重量和制造误差也增大［1，3］，这对球形砂轮的制造和使用将产生较大的制约。

本文提出椭球形蜗杆砂轮，用其替代球形蜗杆砂轮实现连续分度展成磨硬齿面大型内齿圈。参数规格相同时，椭球砂轮比球形砂轮尺寸小，研究表明，椭球砂轮比球形砂轮能更高效、精确、经济地磨削内齿，是前景更好的新型砂轮。

1 椭球蜗杆砂轮的螺旋面方程

1.1 砂轮坐标系与工具坐标系的转换

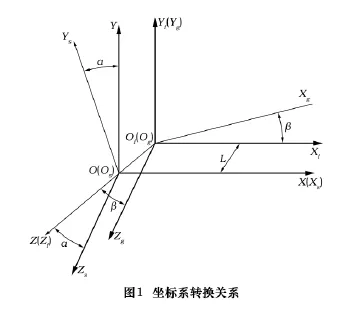
无论是金属坯椭球砂轮(附金刚石磨粒层)还是刚玉椭球砂轮，都涉及椭球蜗杆的生成(加工)，因此，要推导出砂轮修整器坐标系与蜗杆坐标系的转换关系，各坐标系的关系如图1所示。

图1中σ(o－xyz)为固定坐标系，其x轴与蜗杆轴线重合;坐标系σg(og－xgygzg)与砂轮修整器(在专用机床上)固连;坐标系σs(os－xsyszs)与椭球蜗杆固连;σg坐标系先经辅助坐标系σf(of－xfyfzf)向σ坐标系转换，再由σ坐标系向σs坐标系转换得到:

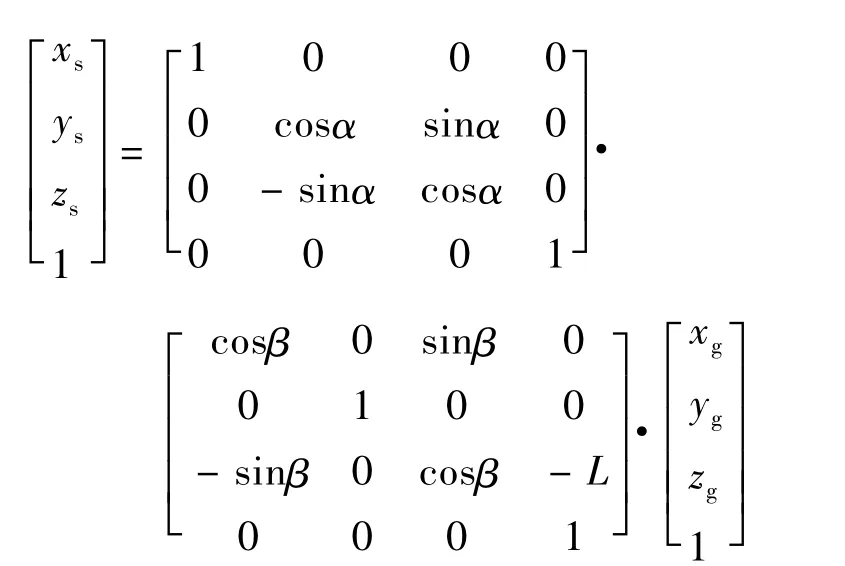
则得到蜗杆砂轮与修整器之间的坐标转换矩阵:

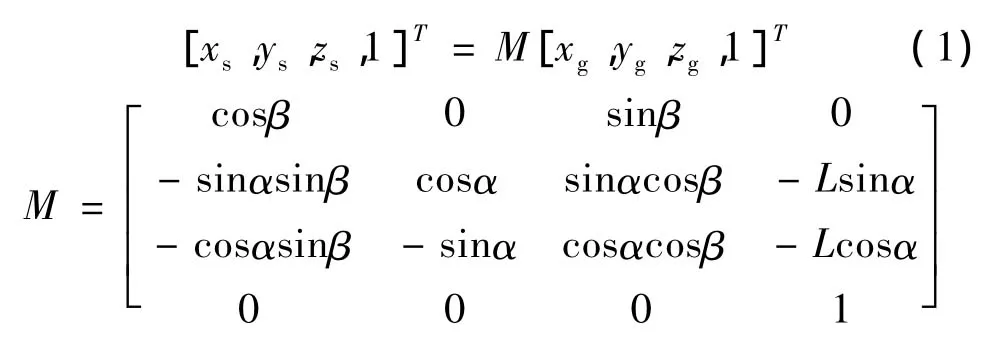
式中:α为椭球砂轮转角;β为砂轮修整器的转角，β=α/Z0;Z0为椭球砂轮轴向当量齿轮齿数;L为砂轮中心与修整器中心的偏离量。

1.2 椭球基螺旋面方程

p(xg，yg，zg)=(0，0，R)为椭球螺旋线上任一啮合点，由式(1)得球基螺旋线方程为

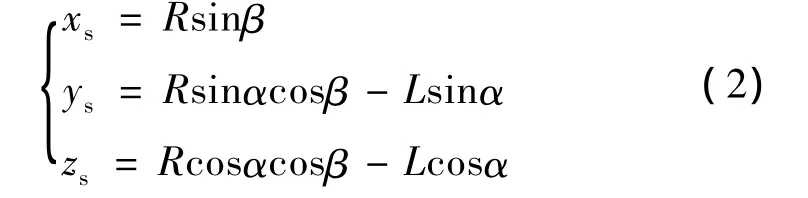
式中:R为经点p的一个截面圆，其圆心oh到点p的距离在水平面上投影值。

如果椭球砂轮法剖面齿轮为渐开线齿廓，则在xgogzg坐标面内的当量齿轮齿廓方程为

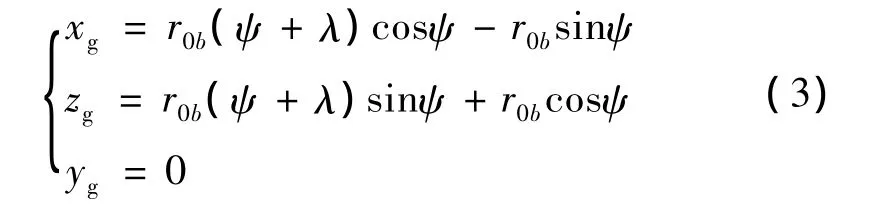
式中:r0b为椭球砂轮当量齿轮基圆半径;ψ为自变量;λ为椭球砂轮当量齿轮齿廓参变数，λ=invγ+π/(2z0);γ为轴剖面齿形角。

将式(3)代入式(1)就可推导出当量齿轮为渐开线齿廓的椭球基空间螺旋面方程为

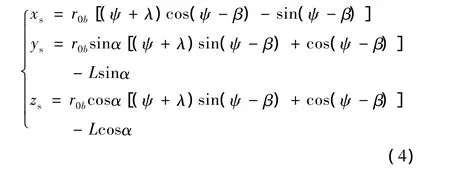
1.3 椭球砂轮的螺旋线升角

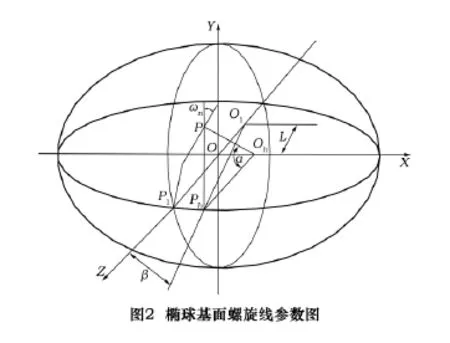
如图2所示，p为椭球螺旋面上任一点，其所在的螺旋线方程为式(2)，点p在xoz内的投影点为ph(，)，也即op=R(R为p所在水平面圆半径);由hhh图示几何关系不难求出点p的矢量式，对点p的矢量式求导，就得到其切向矢量式为

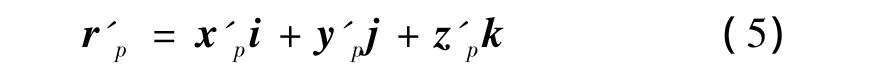
与式(5)所对应的方程组为

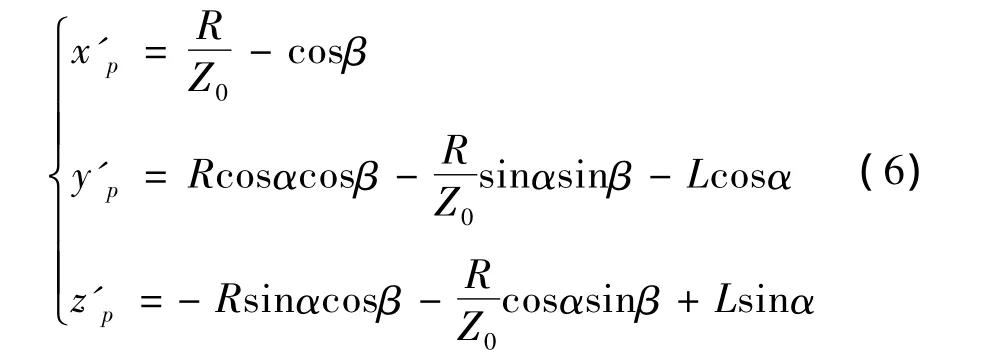
图2中，过点p的端截圆在点p的单位矢量为rop=sinαj+cosαk，对点 p的单位矢量求导，得到点 p单位矢量的切线方程为

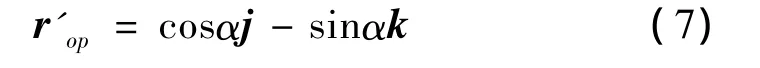
定义r′p与r′op的矢量夹角ωn为点p所在椭球面螺旋线的螺旋升角，其解析式为

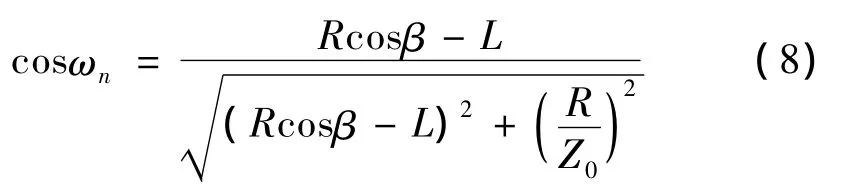
由余弦与正弦的关系及R=m0Z0/2可得:

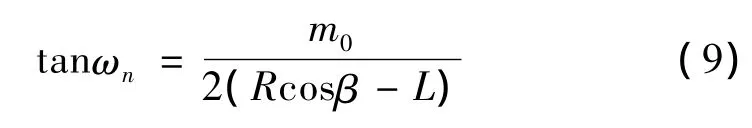
式中:m0为椭球砂轮的轴向当量齿轮模数。当β=0时，有ωn=ω0，称ω0为螺旋线的名义升角;此时点p位于最大直径处。因此，若减小β和L值，增大R值就会使ωn值减小，而ωn值越小，椭球砂轮的理论误差越小。

2 椭球砂轮的法向等值周节

2.1 法向不等值周节对磨齿的影响

椭球砂轮法剖面的齿轮称为法向当量齿轮，其齿形称为法向齿形。由于椭球砂轮螺旋线升角沿轴向变化，螺旋线升角越大，其与名义螺旋线升角的差值越大，所以椭球砂轮的法向当量齿轮理论上是一个不等周节的非圆齿轮，而且每个齿的齿形也不相同［2］。然而，对内齿圈磨削加工精度影响最敏感、最大的是砂轮法向当量齿轮的周节误差，所以，要探讨把法向不等值周节转化为法向等值周节的实用方法，为此，要从与不等值周节相关的几何量之间的关系着手研究。

椭球砂轮磨削大内齿圈的过程相当于其当量齿轮与大内齿圈的啮合过程，当磨削直齿内齿圈时，砂轮轴线需倾斜一个安装角ω0。砂轮法向坐标系与轴向坐标系相对关系如图3所示。

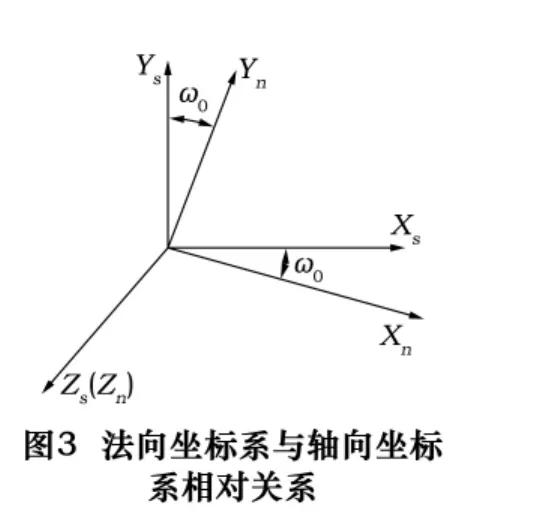
轴向坐标系向法向坐标系转换的矩阵为

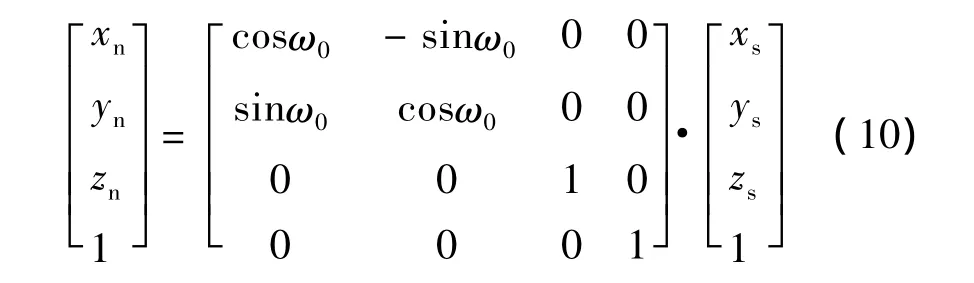
将式(2)代入式(10)可得到:

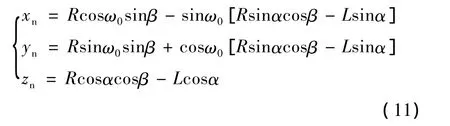
令式(11)中yn=0，可整理出:

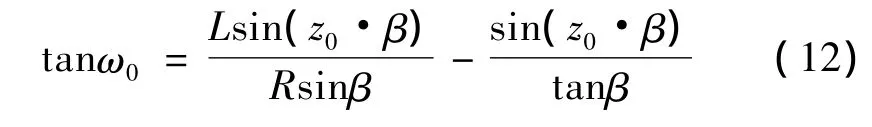
螺旋线绕砂轮轴线的升程规律如图4所示。螺旋线的第1、2、3 圈与法剖面的交点分别为 a、b、c，弧长就是欲求的法向周节，即(mn为椭球砂轮法向当量齿轮模数)。从图几何关系知，以及=(Rcosβ －L)(2π － α)显见，椭球砂轮的法向周节误差产生的基本原因是其螺旋升角值与名义螺旋升角值不相等。

2.2 法向等值周节的形成方法

要提高椭球砂轮磨齿质量，就要消除其法向齿轮周节的变化，并减小法向齿形的变化。因此，要找出消除法向周节误差的方法，即探讨α、β在何条件下变化可实现砂轮法向周节保持等值。由前述各弧长之间的几何量关系易得出:

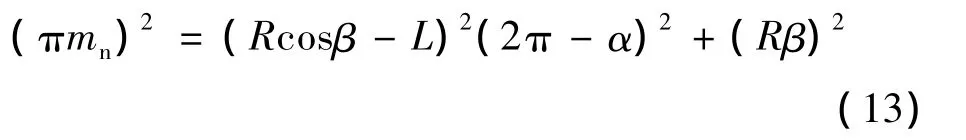
式中，R、L为常数。要使椭球砂轮法向周节保持常值，只能在椭球蜗杆的制造过程中找方法。由式(13)可知，当椭球蜗杆转过α角时，为使πmn值不变，加工工具在转过β角基础上应再增加或减少一个附加转角Δβ，即实际转过 β′=β ± Δβ，右旋蜗杆取“－”。β′或Δβ值由式(13)解出。法向周节等值也能使法向齿形差减小。称这种修正方法为“差动转角法”。

2.3 差动转角计算实例［4］

在自行改造的专用数控机床上加工4种椭球蜗杆［4］，蜗杆转过第1、2、3圈时，工具的理论转角分别为β1、β2、β3;所对应的差动转角分别为 β′1、β′2、β′3，其结果见表1。

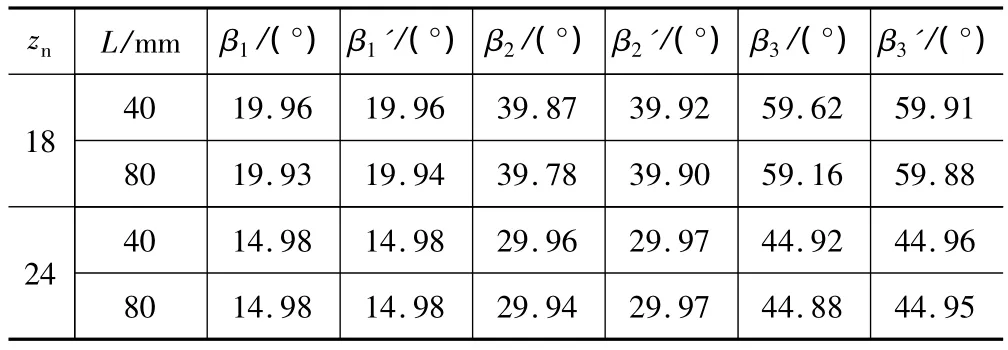
表1 满足法向齿轮等周节的β′值

3 法剖面当量分度圆的圆度控制

3.1 法剖面分度圆的圆度

椭球砂轮法剖面是个椭圆齿轮，其圆度误差会造成被磨削齿轮的齿形误差，用椭圆齿轮的当量分度圆与标准分度圆的差值表示法剖面的“圆度”。椭球砂轮法剖面的当量分度圆曲线可由式(2)求得，其坐标系可参见图2。

设点p(x0，y0，z0)为螺旋线上任一动点，由式(10)得到点p在法向坐标系的坐标为

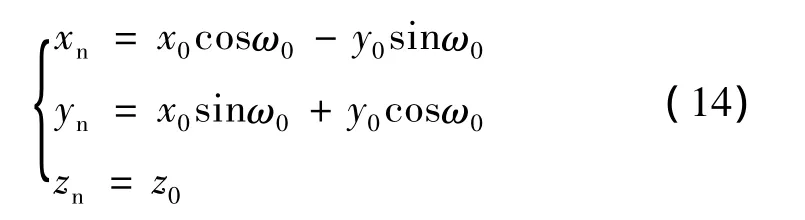
令yn=0，并依据与式(2)的对应关系可求得砂轮的椭球面在其法向面的投影方程为

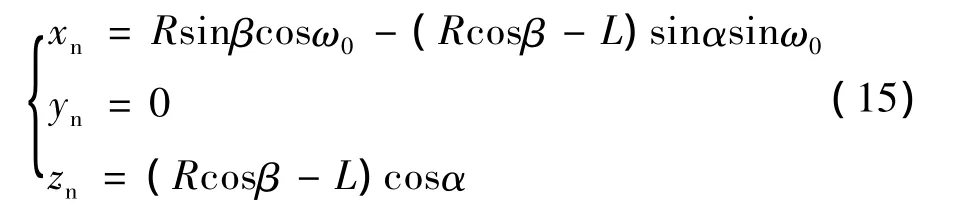
由上述可知，法剖面内的圆度误差随法剖面当量齿轮齿数zn增大而减小，随着偏离量L值增大而增大。因此，设计时应综合考虑zn和L值。当L=0时，椭球砂轮成为球形砂轮，理论上讲，球形砂轮不存在法剖面内圆度误差［3］。

3.2 法剖面圆度误差量计算

依据yn=0与式(14)可得到:

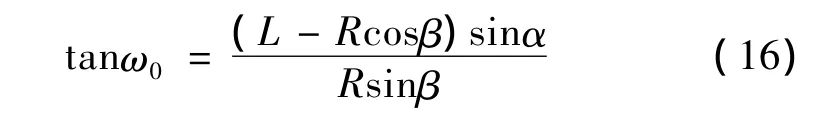
因为ω0、L、R通常为常数，任给一个β就可由式(16)解出一个α，再将β和α代入式(15)就可求出椭球面上一个点的坐标。如果给出一系列β和α值，就可得到椭球体的法剖面截曲线，该截曲线理论上是以距椭球几何形心距离为L的一点为圆心，以R为半径的圆弧［2］。如果用ΔR表示圆度误差值，计算式为:

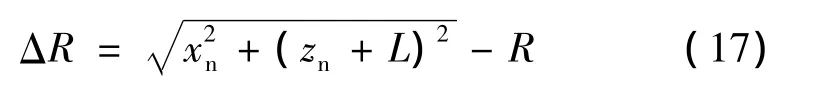
通过计算结果可知，距离z轴越近的点其圆度误差越小［4］，也就是说椭球砂轮的轴向尺寸越小(砂轮越短)，其圆度误差越小。

4 结语

提出了椭球形蜗杆砂轮，阐述了椭球砂轮磨削硬齿面大内齿圈的机理，归纳出椭球砂轮比球形砂轮更优势依据。通过坐标变换求得椭球砂轮螺旋面方程，给出椭球砂轮螺旋升角计算式，指出螺旋升角越小，椭球砂轮几何误差越小。由于椭球砂轮螺旋升角大于球砂轮螺旋升角，所以，椭球砂轮在误差控制方面难于球形砂轮。

探讨了椭球砂轮两个棘手问题:法剖面当量齿轮周节的不等值性;法剖面当量分度圆的圆度误差。给出了在椭球砂轮制造过程用“差动转角法”将法向不等值周节转化为等值周节的方法。给出了控制法剖面圆度误差的措施。

［1］崔云起，胡占齐，李宇鹏.球形滚刀的理论研究［J］.机械工程学报，1996，32(2).

［2］崔云起，胡占齐，王海艳，等.椭球形滚刀若干理论问题［J］.工具技术，2009，43(8).

［3］李宇鹏.球形蜗杆砂轮的磨齿原理及其球基螺旋面参数［J］.机械工程学报，2002，38(6).

［4］崔云起，胡占齐，等.球形及椭球形滚刀及其数控铲磨机床究［J］.机床与液压，2009，37(12).