基于神经网络的机床－工件系统热误差补偿技术研究

满忠伟 汪世益

(①山东山推机械有限公司，山东济宁 272023;②安徽工业大学机械工程学院，安徽马鞍山 243002)

机床热变形对工件加工精度的影响很大，热误差是最大的误差源，可达机床总误差的70%左右［1］。因此，控制热误差是提高机床加工精度的关键技术。误差补偿技术可以在不提高机床自身零部件精度的条件下，使工件的加工精度大幅度提高［2－3］。

机床热误差在有效补偿的前提下能够对某一温度场下的机床热误差进行准确的预报，然后根据预报值进行补偿。这就要求尽可能准确地进行热误差建模，即建立机床热误差与温度之间的关系，从而在实时补偿过程中用温度值来预报热误差。热误差建模的方法很多，选择不同的建模方法对误差补偿效果有非常大的影响。热误差很大程度上取决于加工条件、加工周期、冷却液的使用以及周围环境等诸多因素 ，因此热误差呈现非线性及交互作用。神经网络理论是利用工程技术手段模拟人脑神经网络结构和功能的一种非线性动力学系统［4］，它具有集体运算能力和自适应的学习能力，以及很强的容错性、鲁棒性，善于联想、综合和推广，目前以神经网络为代表的智能补偿技术已运用到误差建模中［5－6］。以往的热误差模型以机床为研究对象，忽略了工件的热变形对加工精度的影响。本文以机床－工件系统为研究对象，应用BP神经网络理论建立机床－工件系统的热误差模型，并在此基础上提出误差补偿策略。

1 机床－工件系统的热误差分析

机床的热误差主要是由于机床工作时复杂的温度场造成机床各部件变形即机床的热动态过程而引起的。机床运转过程中，运动部件在内部和外部热源作用下，产生热量并传给机床各部位产生温差，使各零部件产生热变形，造成加工精度下降。

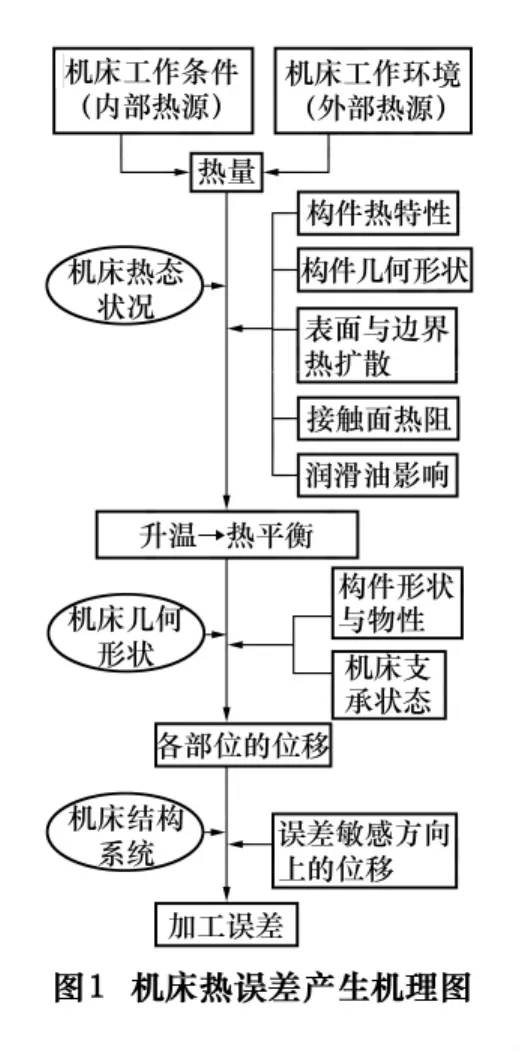
机床中的内部热源包括设备运行中的运动副产生的摩擦热、加工中的切削热和动力源的发热;外部热源主要是环境温度的变化。机床各部件通过热传导、热对流和热幅射3种方式进行热交换，由于零件形状、结构及约束条件不同，引起拉、压、弯、扭等各种热变形，造成与加工精度相关的各零部件产生不同程度的热位移，最终导致机床加工精度下降［7］。机床热误差产生机理如图1所示。机床各种内部热源的发热量及环境温度均随具体的加工情况、时间而变化，同时机床有一定的热容量，其温升必然存在时滞现象，所以根本上说，机床热变形是随时间变化的非恒定现象。

工件热误差主要是由于工件在加工过程中产生大量的切削热，其中一部分切削热传入工件，使工件产生热膨胀变形，因此，工件是在热膨胀的状态下进行加工，而工件加工完成后，在常温状态下冷却，工件又冷却收缩变形。所以，工件的热变形(热膨胀变形和冷收缩变形)对加工精度影响巨大。

2 机床－工件系统热误差神经网络建模

数控机床热误差补偿的关键是建立精确的热误差模型，热误差模型是否合理直接影响补偿的效果。本文以数控立车加工回转支承滚道为例，选择了合理的输入和输出参数，建立机床－工件系统的BP神经网络热误差模型，并对该模型进行训练、修正和测试。

2.1 机床－工件系统热误差神经网络模型

机床－工件系统的热误差BP神经网络模型的建立主要有2个方面:一是神经网络热误差模型输入和输出参数的选择;二是确定热误差神经网络模型的结构。

输入和输出参数直接影响热误差模型的精度。输入量选择的太少，可能造成信息的缺失，选择的太多或不合理，测量的时间和成本就会增加。以往的热误差模型都是以机床为对象，机床的热误差源与机床的结构有关，但引起加工热误差的热敏感区域主要有床身、主轴和丝杠，所以热误差模型的输入参量为床身、X轴丝杠、主轴和切削液的温度，输出参量为主轴径向位移。由于在金属加工过程中产生大量的切削热传入工件，引起工件热变形，且热变形的大小与工件的几何尺寸有关，所以工件的温度和几何尺寸也是影响热误差的重要因素。综上所述，加工热误差影响因素有3个方面:机床热敏感区温度、工件温度和几何尺寸。所以热误差模型的输入参数选择机床热敏感区的温度、加工工件的温度和工件的几何坐标，输出参数选择工件的误差值。

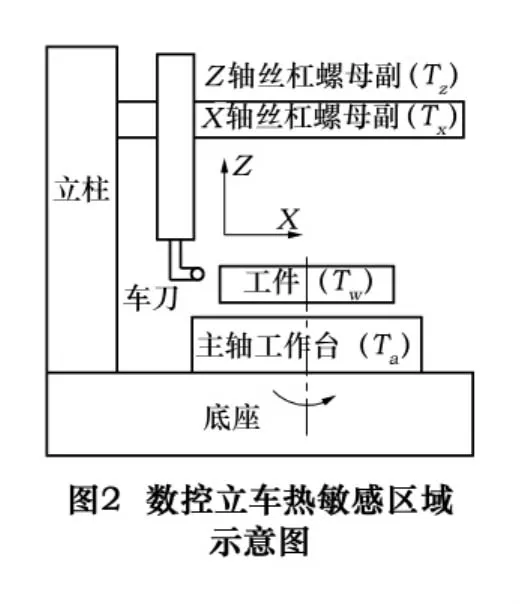
通过以上理论分析，以数控立车加工回转支承滚道(干式车削)建立热误差模型，数控立车热敏感区域的温度如图2所示。为了减少模型的输入参数，考虑车床立柱热变形很小，忽略床身对热误差的影响，所以影响加工热误差的因素主要有丝杠、主轴和工件的热变形及工件的几何尺寸，它们分别对应的输入参数是:X轴和Z轴丝杠螺母温度Tx和Tz、主轴轴承温度Ta、回转支承(工件)温度Tw、回转支承在X和Z轴方向的坐标X和Z。输出量以冷却后的回转支承为对象，由于数控立车切削时在X和Z两个方向移动，选择回转支承滚道面X和Z的方向的误差值ΔX和ΔZ作为输出参数。

机床－工件系统的热误差模型与机床热误差模型相比，输入参量考虑了加工过程中工件热变形对热误差的影响，误差模型的输入更加全面准确;由于加工精度最终以成形工件的精度为标准，所以机床－工件系统热误差模型输出参量选择工件加工后的误差量，显然优于以机床主轴径向位移误差作为输出参数。

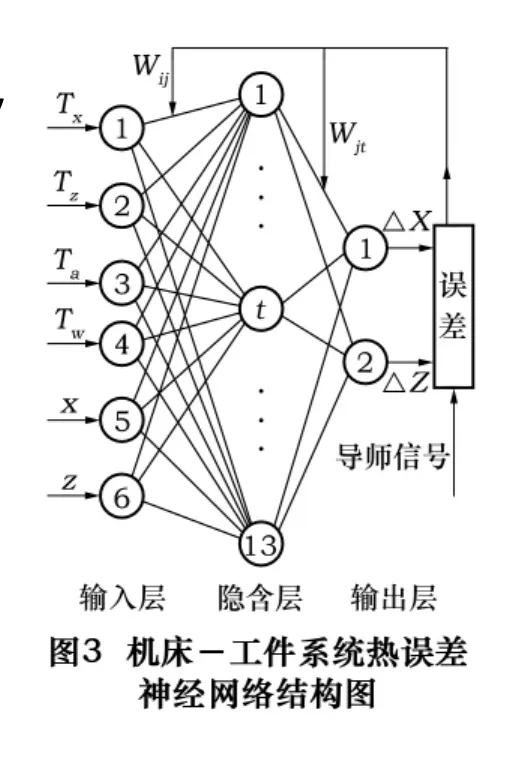
神经网络的结构对整个神经网络的特性具有决定影响。机床－工件系统热误差模型采用3层的BP神经网络结构。通过以上对数控立车加工回转支承滚道的分析，该模型的输入层和输出层分别有6个和2个节点，中间隐层节点数的选择对网络的学习和计算特性具有非常重要的影响，是该网络结构成败的关键。考虑到机床－工件系统误差模型的特性，我们认为热误差是机床和工件温度及工件几何坐标的连续函数。根据Kolmogorov定理［8］，若3层神经网络的输入层有m个节点，输出层有n个节点，则中间隐层应有2m+1个节点，所以中间隐层的节点数为13个。因此，机床－工件系统的热误差神经网络模型的结构为6－13－2，模型结构图如图3所示。

2.2 热误差神经网络模型仿真

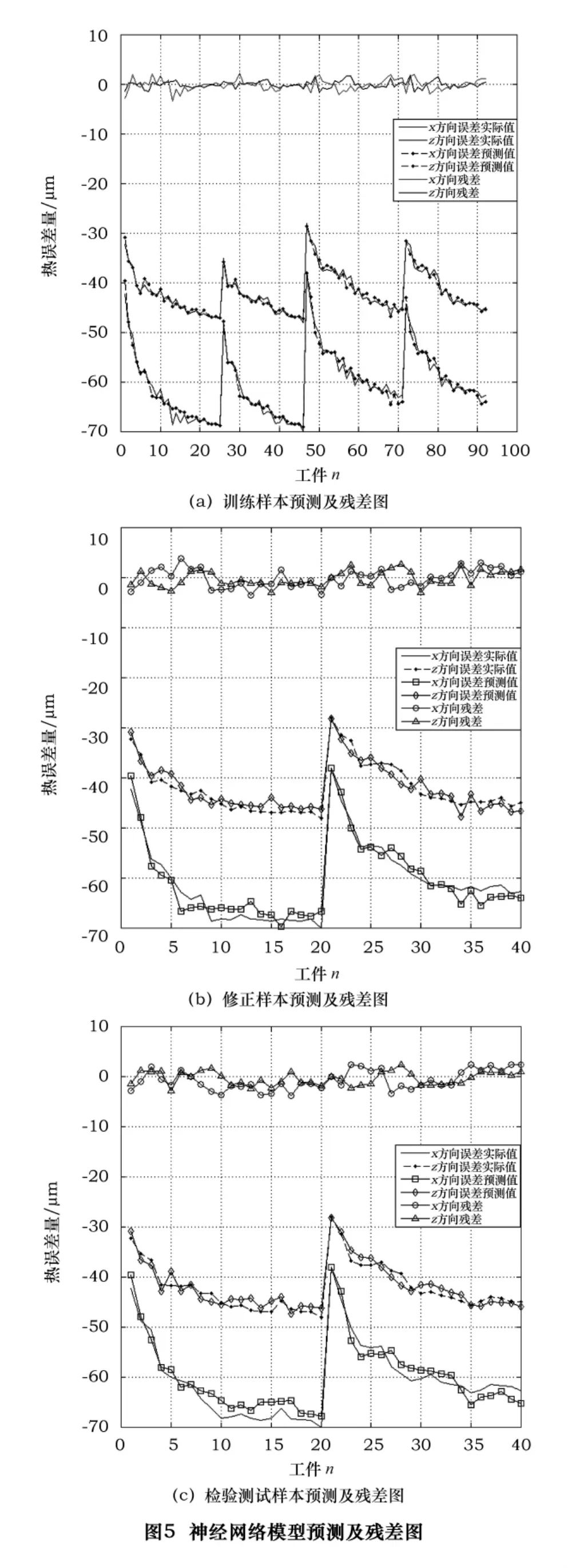
机床－工件系统热误差模型建立后是没有预测能力的，必须通过一定量的实验(实测)数据进行训练、修正，模型经过测试在误差范围内才可应用。以CK5116型数控立车加工回转支承(型号010.40.1120)的滚道为应用实例，如图4所示。针对机床－工件系统热误差模型，采集172组输入和输出数据(输入和输出数据组结构如图3所示)。采集的方法如下:用热电偶传感器测量主轴和丝杠的温度，用红外测温仪测量工件的温度，工件的几何尺寸由数控系统的编程程序中输出。工件加工误差采用离线测量的方法，即回转支承滚道加工冷却后，在常温下测量工件在X和Z两个方向的误差值。采集的172组数据中，92组数据用于模型训练，修正和测试数据各40组。机床－工件系统的热误差模型的训练、修正及测试［9］如图5所示。图5所示的热误差模型的预测效果如表1所示。

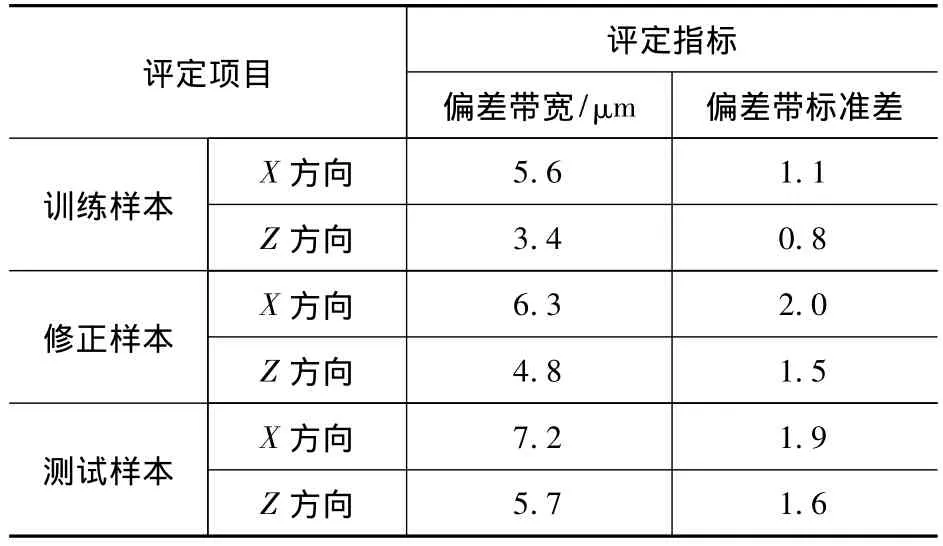
表1 热误差模型的预测效果

由表1可知，模型训练、修正及测试的偏差带宽在8 μm以下。神经网络热误差模型经过训练和修正后，对测试样本进行检验，测试样本的偏差带宽与标准差和修正样本相比，相差很小。因此，机床－工件为系统的热误差神经网络模型经过训练修正后对热误差有较好的预测能力。

3 机床－工件系统热误差补偿

3.1 机床－工件系统的热误差补偿策略

为了完成机床－工件系统的热误差补偿，本研究基于数控编程软件反向补偿原理［10］，设计了数控机床热误差补偿系统，实现刀具的偏移，即刀具与工件之间在运动的逆方向上偏移1个大小与误差接近的数值。补偿系统实施方案如图6所示。

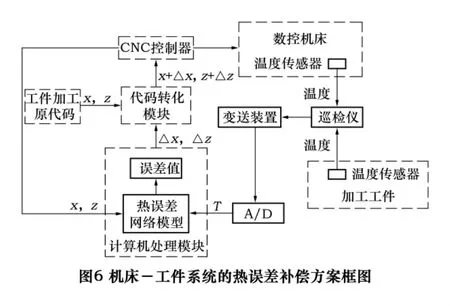
补偿方案如下:当工件加工进入精加工时，开始进行误差补偿，且一次补偿成功。进入补偿阶段，温度传感器采集机床和工件的温度值，通过各个通道把温度值输送到巡检仪，形成温度文件，采集温度值经过调理、A/D转换变成计算机可接收的数字信号，设置与计算机处理模块的端口及通讯参数，计算机接受巡检仪发送来的温度数据;同时，计算机拾取控制系统的几何坐标信号，经过计算、处理输出热误差补偿值。代码转化模块搜索加工源代码文件中需要补偿的代码，搜索完成后记录该代码，调用计算机计算出来的误差值，将误差值求反并修正记录下来的代码，生成具有热误差补偿的新代码，然后将新数控代码文件传送到数控系统，从而控制传动系统执行修改后的数控代码程序。

3.2 机床－工件系统的热误差补偿效果

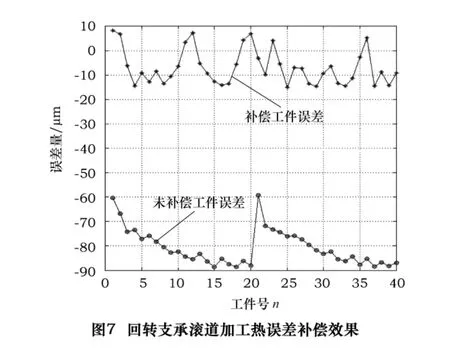
根据以上建立的机床－工件系统热误差模型和设计的补偿系统方案，对CK5116型数控立车加工回转支承(型号010.40.1120)的滚道进行热误差补偿。为了检验补偿效果，把需要加工的80个回转支承分为2组，每组40个，同时在2台数控立车上加工。第一组不进行误差补偿，第二组采用设计的补偿系统及补偿模型，加工完成后对冷却的回转支承滚道误差测量结果如图7所示。由图7可知，经过补偿的工件的误差的精度控制在±15 μm以内，与未补偿的工件相比，精度提高了80%以上。

4 结语

大型工件的干式切削热变形对加工精度影响很大，文章综合分析了热误差对加工精度的影响，建立了机床－工件系统的热误差神经网络模型，并对该模型进行训练、修正和测试，确定模型有强的预测能力，提出了机床－工件系统热误差的软件反向补偿方法和补偿策略。最后以某型号大尺寸回转支承滚道加工为例进行误差补偿，结果表明，经过补偿后的回转支承滚道的加工精度大幅度提高。

［1］BRYAN J B.International status of thermal error research［J］.Annals of CIRP，1990，39(2):545 －646.

［2］倪军.数控机床误差补偿研究的回顾及展望［J］.中国机械工程，1997，8(1):29 －33.

［3］YANG S，YUAN J，Ni J.Accuracy enhancement of a horizontal machining center by real－ time compensation［J］.Journal of Manufacturing Systems，1996，15(2):113 －124.

［4］焦李成.神经网络系统理论［M］.西安:西安电子科技大学出版社，1990.

［5］MIZE C D，ZIEGERT J C.Neural network thermal error compensation of a machining center［J］.Precision Engineering，2000，24(4):338 －346.

［6］杨建国，张宏韬，等.数控机床热误差实时补偿应用［J］.上海交通大学学报，2005，39(9):1389 －1392.

［7］吴昊，杨建国，等.精密车削中心热误差鲁棒建模与实时补偿［J］.上海交通大学学报，2008，42(7):1064 －1067.

［8］胡伍生.神经网络理论及其工程应用［M］.北京:测绘出版社，2005.

［9］闻新，周露，等.MATLAB神经网络仿真与应用［M］.北京:科学出版社，2003.

［10］汪世益，黄筱调，等.风电回转支承滚道切入磨削的砂轮修形［J］.中国机械工程学报，2009，20(3):275 －279.