类比法在物理化学热力学函数关系式记忆中的应用

郭玉鹏

(吉林大学化学学院物理化学系 吉林长春 130012)

物理化学作为大学化学类专业的一门重要基础课，理论性很强。具有概念多、公式多、原理多，知识逻辑性强、与其他学科知识联系密切的特点，是学生普遍感到难学的一门课。在教学过程中, 大量的函数公式常使学生感到困惑, 如公式的适用前提、公式的形式等。学生反映这部分内容就像是数学符号的游戏, 记忆困难，难以便捷地应用在分析和处理问题上。因此在课堂教学过程中容易显得枯燥，影响学生学习的积极性，在一定程度上会影响教学质量的提高。

在教学过程中，函数关系式的推导和形式的记忆对分析和处理问题有重要意义，是教学的重要内容。通常清晰的思路、合理的路线、正确的推导过程可以培养学生的抽象思维能力和逻辑推理能力，增强学生运用数学解决问题的意识和能力。目前，我们采用的教材中主要包含热力学、动力学、电化学、胶体和界面化学等四大部分内容[1]。其中，热力学占据相当重要的地位，涉及了系统的热力学能(U)、焓(H)、熵(S)、亥姆赫兹函数(A)、吉布斯函数(G)，以及可由实验直接测定的系统的压力(p)、体积(V)、温度(T)等最基本的热力学函数。2009年，大连理工大学王旭珍等报道了通过从基本公式出发，结合偏微商的关系进行公式的推导，可以缓解热力学函数关系式推导过程中的教学难点[2]。这种思路不仅对教师适用，而且能帮助学生更好地理解和学习其他专业课。然而，由于课时关系及学生数学能力的差异性，能掌握最基本的原始公式，基本的推导方法和思路对学生来说已经是很高的要求。加之在学生考核过程中的时间限制，多数学生很难在有限的时间推导出所需的正确函数关系式并对问题进行准确的计算和讨论，影响了考核效果。因此，公式的准确记忆就显得尤为重要，物理化学课程公式繁多, 如果单纯要求学生采用填鸭式的记忆, 难度大, 效果不理想。国内外曾有人对物理化学中热力学部分的公式的记忆方法进行了探讨，目前主要采用两大方法，一种是图像法，另外一种是非图像法。前者如李振川所总结的图示法[3]，王树国等人给出的坐标记忆法[4]，阿里木江等人给出的状态函数正方形法[5]；后者所涉及的具体方法更为灵活多样，如尹春玲提出的利用特性函数记忆法来掌握热力学关系式[6]和陈家纬等人提出的利用一句日常英语对话法来掌握热力学的基本关系式和热力学函数的麦克斯韦关系式[7]。细心的读者可以发现，目前所报道的文章(无论是图像法还是非图像法)中，主要是针对物理化学热力学函数中的基本关系式和麦克斯韦关系式的推导和记忆；对于物理化学其他部分如动力学、界面化学所涉及的公式几乎没有报道。此外，对图像法而言，虽然可以帮助人们加深记忆，但对于初学物理化学的学生，图形绘制和记忆并不是很方便。物理化学的热力学、动力学、电化学和界面化学等内容的公式不是孤立的，公式之间具有普遍联系的特点。结合类比法能够帮助学生解决热力学、动力学和界面化学等公式中的记忆形式模糊、复杂等问题。本文将多年教学过程中的心得总结成文，以期使公式的记忆形式更加灵活，牢固，量更少, 并期望和同行交流。

本文主要讨论典型的具有相似形式的公式的记忆，以及利用物理化学中函数量纲的特点简化公式的记忆。

1 理想气体状态方程形式的公式

理想气体状态方程(式(1)) 是最常用的公式，最类似的形式为van′t Hoff的渗透压公式(式(2))。

pV=nRT

(1)

式中p为压力，V为体积，n为物质的量，R为气体常数，T为温度。

ΠV=nBRT

(2)

式中Π为渗透压，V为溶液体积，nB为溶液中溶质的物质的量。

此外，有些公式虽然没有式(1)的形式，但是经过简单的分析、处理，同样可以转化成相似的形式来记忆。例如，热力学相平衡中的任意纯组分的两相平衡公式Clapeyron 方程(式(3))。

(3)

式中p、T分别为纯组分二相平衡时的压力和温度，ΔVm为相变前后的摩尔体积增量，ΔHm为摩尔相变焓变。

虽然式(3)与式(1)有很大的差异，但是通过处理式(3)可以很容易地得到式(4)。

(4)

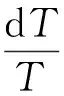
在界面化学部分，描述弯曲表面上的蒸气压的Kelvin公式(式(5))同样可以采用理想气体状态方程形式记忆:

(5)

式中R为气体常数，T为温度，pr、p0分别为曲率半径为r的弯曲表面的液体和平面液体的饱和蒸气压，M为液体的摩尔质量，ρ为液体的密度。

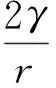
以上3个公式(式(2)、式(4)和式(5))均可用理想气体状态方程的形式来记忆。这种相似性是建立在客观世界各种现象的普遍联系基础之上的。通过比较相同点和关联性，既可加深对物理化学本学科知识点的理解，也能使学生对自然规律的普遍联系有更深入的认识[8]。为了更好地理解理想气体状态方程(式(1))的形式，并利用其辅助记忆其他的公式，还需掌握下面的内容。

2 具有能量量纲的函数及其组合函数在公式记忆中的应用

理想气体状态方程是描述理想气体p、V和T等状态函数定量关系的表达式，从另外一个角度来看，也是相对能量守恒形式的一种表达。其原因如下，理想气体在等压可逆膨胀过程中所做的体积功的表达式如式(6)所示。

δW体=-pdV，积分式W体=-pΔV

(6)

由式(6)可见，p和V的乘积是一种能量的表达式，而R与T的乘积也是能量的表达式。在物理化学中，具有能量量纲的函数如下：热力学能(U)，焓(H)，亥姆霍兹自由能(A)，吉布斯自由能(G)等。此外，还有一些函数组合在一起同样具有能量的特征，如温度与熵的乘积(TS)，电化学中的nEF等。了解这些与能量量纲有关的变量同样有利于公式的记忆。在热力学中，H=U+pV、G=H-TS、A=U-TS3个定义式就是有关体系具有能量量纲的函数之间的最直接的关系表达式，包括由它们推导出的4个热力学基本方程(式(7)～式(10))。

dU=TdS-pdV

(7)

dH=TdS+Vdp

(8)

dA=-SdT-pdV

(9)

dG=-SdT+Vdp

(10)

在以上有关具有能量量纲的函数关系式中，U、H、A、G可以单独存在，而压力p和体积V的乘积形式pV，熵S和温度T的乘积形式ST，以及前面提到的RT形式和nEF形式，成为具有能量量纲的组合函数的形式。因此，合理利用这些具有能量量纲的函数及其组合函数，有助于记忆其他公式。如式(11)为等压下电池的温度系数的微分表达式。

(11)

结合数学中比例的特点，很容易看出式(11)中比例的内项积和外项乘积分别为具有TS和nFE能量形式的表达式。于是，给出左边的问题项后，等式的右侧完全可以根据具有能量量纲的函数间的组合分别写出相应的分子和分母项。

此外，在热力学公式中，由4个热力学基本方程(式(7)～式(10))，利用其二阶混合偏导数得出的Maxwell关系式(式(12))中存在大量偏微分的形式：

(12)

从式(12)中不难发现T、S，p、V都是以偏微分形式且对应地出现在等号两侧的比例内项或外项。此外，偏微分的下标和偏微分分式中的分子项也同样是成对出现的。Maxwell关系式(式(12))主要还是经过基本关系式的推导得到，要正确应用必须经过正确的推导过程。虽然具有能量量纲的函数及其组合函数形式的方法不能用来推导公式，但是可以用其验证推导的准确性并辅助记忆。此外,在诸多热力学关系式中，大量的具有能量量纲的函数及其组合函数出现其中，细心的读者可以自行找寻并进行检验。

3 函数量纲特性在公式记忆中的应用

物理化学课程中涉及的关于具有能量量纲的函数和函数关系式众多，在关系式中经常看到T，T2，R，RT等形式存在其中，如式(12)～式(14)。 这些形式经常会给学生的记忆带来困难。公式中函数和函数关系式并不是数学符号游戏，函数的本身及相互关系并不是孤立的，而是在对客观世界内在规律普遍联系的基础上抽象出来的一种形式。每个符号和每个函数都具有一定的物理意义，函数的量纲是其意义的一种直接表现形式，充分了解这一点对函数关系式的推导和记忆也会有所裨益，下面通过式(12)～式(16)加以说明。

式(13)为理想气体状态由(p1，V1，T1)变化到(p2，V2，T2)的熵变求算公式。我们知道，熵的量纲与等压热容Cp，等容热容CV和nR的量纲相同，因此，在式(13)中自然对数之前的变量均为与熵量纲相同的变量。类似的利用函数量纲的特点还可参见式(14)(Gibbs-Helmholtz公式)，在等式右侧的分母上，学生常为是T还是T2，引起记忆困难。从量纲的特点我们可以看到，等式左侧为能量比温度的平方形式，因此右侧也应具有相同的量纲，这样就能很清楚地记忆等式的右侧分母应是具有T2的形式。利用函数的量纲特性来简化公式的记忆在动力学的公式中也能看到，如在过渡态理论计算反应速率常数的公式(式(15))中，2个e的指数项出现了具有相似形式的两个分式，一个是熵变除以R的形式，一个是焓变除以RT的形式。通过上面所说的熵、焓的量纲分别对应的是R和RT的量纲，结合自然对数或指数项是无量纲的特点，很容易对式(15)中出现的分式进行区分和准确记忆。

(13)

(14)

(15)

物理化学公式多，记忆复杂，上面通过举例分别说明了物理化学公式记忆的3种方法，这3种方法不是孤立的而是紧密联系的。例如统计热力学中波尔兹曼分布公式(式(16))和动力学部分的阿累尼乌斯方程(式(17))具有相似的形式，而其e指数项差异性的记忆可以通过函数的量纲特性来记忆。例如式(17)，Ea和RT的量纲均为J·mol-1，式(16)中εi和kBT的量纲均为J， 这样才能使e的指数项为无量纲的数值。

(16)

k=Ae-Ea/RT

(17)

4 结语

当今时代的学生思想活跃，接受新事物的能力强，学习知识的渠道多，视野宽广。教师在讲课时，一方面必须能在理论上剖析透彻，灵活运用热力学、动力学的基本原理讲授函数关系式的推导方法，培养学生的抽象思维能力和逻辑推理能力，增强他们运用数学意识的过程；另外一方面，运用类比法对物理化学公式中的规律进行观察和总结，以理解学习代替记忆学习，在简化公式记忆的同时，既可加深对物理化学知识点的理解，也可以使学生对自然规律的普遍联系有更深入的认识，更好地提高学习效果。

[1] 傅献彩,沈文霞,姚天扬,等.物理化学.第5版.北京:高等教育出版社,2006

[2] 王旭珍,靳长德,王新平.大学化学,2009,24(5):69

[3] 李震川.化学通报,1982(1):48

[4] 王树国,袁誉洪,李金林,等.广东化工,2010,37(201):168

[5] 阿里木江K·艾拜都拉,开丽比努尔·艾山,朱玉军.北京教育学院学报,2004,2(2):5

[6] 尹春玲.平顶山师专学报,2002,17(5):94

[7] 陈家纬,杨忠芳.张德会.中国地质教育,2005(4):410

[8] 张保安,严凤娇.高等理科教育,2009(1):44